Семестр 04 / Физика / 21-24

21.Электрический дипольный момент. Электрическое поле диполя. Электрический диполь во внешнем поле.

ДИПОЛЬ – система, состоящая из 2х разноименных зарядов.

p = ql – электрический момент диполя.

Вектор р направлен по оси диполя от отрицительного заряда к положительному. Где q>0 и l – вектор направлен в туже сторону что и р.

l – расстояние между зарядоми. А в целом формулы ещё может выглядеть так: p=Σqiri

Эл. Поле диполя.

E(l) = -d/dl, вычислим с помощью нее проекции вектора Е на 2 взаимно перпендикулярных направления, вдоль ортов еr и e.

E(r)= -d/dl = 1/4o * 2pcos/r³

Отсюда модуль вектора Е

E=√Er²+Eν²=1/4o * p/r³ * √1+3cos²ν

При ν=0 и ν=90˚т получим выражения для напряжения поля соответственно на оси диполя (Е║) и перпендикулярно ей (Е┴)

Е║ = 1/4o 2р/ r³

Е┴ = 1/4o р/ r³

При одном и том же r напряженность Е║ вдвое больше Е┴.

Эн. Диполя во внешнем поле.

Энергия т.з. q во внешнем поле равна W=qφ, где φ – потенциал поля в точке нахождения заряда q. Диполь – система 2х зарядов, блин, поэтому его энергия во внешнем поле равна

W=(q+φ+ )+ (q-φ-) = q(φ+ - φ-) – φ± - потенциалы внешнего поля расположения зарядов +q и –q.

φ+ - φ-=dφ/dl * l

где dφ/dl – производная потенциала по направлению вектора l.

W=-pE

Из этой формулы следует, что минимальную энергию диполь имеет в положении p↑↑E (положение устойчивого равновесия). При отклонении из этого положения возникает момент внешних сил, блин,. Возвращающий диполь в положение равновесия.

№22. Поле в диэлектриках. Вектор поляризованности диэлектрика. Связанные заряды.

Полем Е диэлектрике будем называть величинуявляющуюся суперпозицией поля Ео сторонних зарядов и поля Е’ – связанных зарядов.

Е=Ео + Е’

Где Eo и E’ макрополя, т.е. усредненные по физически бесконечно малому объему микрополя соответственно сторонних и связаных зарядов. Е в диэлектрике тоже будет являться макроплем.

Поляризованность Р .

Р – это дипольный момент единицы объема вещества.

Р = 1/∆V ∑ рi

Связанные заряды.

Некомпенсированные заряды появляющиеся в результате поляризации диэлектрика, называют связанныеми. Свобода перемещения таких зарядов ограничена. Они могут лишь смещаться лишь внутри электронейтральных малкул.

Свободные заряды, напротив, могут находиться как внутри, так и вне диэлектрика…

№23. Электрическая индукция.Теорема Гаусса для вектора электрической индукции.

о∫ - интеграл через замкнутую поверхность.

Поскольку источником поля Е являются все электрические заряды (сторонние и связанные), то теорему Гаусса для Е можна записать так:

о∫εoEdS = (q+q’)внутр.

q q’ – сторонние и связанные заряды охватываемые поверхностью S.

Выразим q’ через поток вектора Р (по формуле о∫РdS = -qвнутр.)

Тогда:

о∫εo(E+Р)dS = qвнутр.

εoE+Р = D

Поток вектора D сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонниих зарядов, охватываемых этой поверхностью.

о∫DdS = qвнутр.

№24 Условия на границе 2х диэлектриков для векторов электрической индукции и напряженность электрического поля.

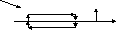
( l – длина обхода контура, τ1 – орт касательной к верхней стенке, , τ2 – к нижней, n – вектор нормали, ε1 – среда 1, ε2 – среда 2.E – это стрелочка со стороны.)

τ 1= τ= - τ2

о∫Bdl = 0 = E1 τ1 * l + E2 τ2 = E1 τ – E2 τ = 0

E1 τ=E2 τ

D = εεoE

D1τ = ε1εoE1τ

D2τ = ε2εoE2τ

D1τ/D2τ = ε1/ε2

На границе нет свободных зарядов.

Рисуем такой же рисунок, только вместо контура там будет «микро» цилиндрик. С векторами нормали через каждую крышку площади ΔS. Высота цилиндрика h стремиться к нулю.

n1 = n = -n2

о∫Dds = D1n1 ΔS + D2n2 ΔS = D1n ΔS – D2n ΔS=0

D1n=D2n

D1n = ε1 εo E1n = D2n = ε2 εo E2n

E1n/E2n = ε2/ ε1