1. Основы работы и расчета на устойчивость центрально сжатых стержней.

И счерпание несушей способности длинных гибких стержней, работающих на осевое сжатие, происходит от потери устойчивости

Работа центрально сжатого стержня:

а — расчетная схема; б — зависимость между нагрузкой и прогибом стержня

При фиксированном N = const, можно подсчитать приращение работ внешних dА_е и внутренних dАi сил. Если dAi > dAe то состояние устойчивое, при dAi <dAe — неустойчивое, при dAi = dAe — критическим.

При изучении проблемы устойчивости стержней приращения работ на возможных перемещениях можно заменить приращениями соответствующих моментов dМе и dМi вследствие их прямой пропорциональной зависимости. При фиксированном N = const приращение момента внешних сил при возможном прогибе с амплитудой n равно dМе = Nn.Внутренних сил dМi = ρEI, где El — жесткость стержня; ρ = -у" — кривизна. Соответствующее критическое напряжение будет иметь вид:

Эта формула справедлива при напряжениях, не превышающих предел пропорциональности s_cr < s _пц, при этом >  √(Е/  _пц). Для мягких строительных сталей  _пц = 20 кН/см2, следовательно l > 100. Для сталей повышенной прочности применимость формулы Эйлера ограничена значением l >85. Следует заметить, что на практике гибкости центрально сжатых стержней (колонн, элементов ферм, рам и т.п.) в большинстве случаев составляют примерно половину указанных предельных.

2. Потеряют устойчивость в упругопластической стадии работы материала с касательным модулем деформации. Формула ф.С.Ясинского.

При l меньше предельных (Для мягких строительных сталей l > 100, для сталей повышенной прочности l >85) стержни теряют устойчивость в упругопластической стадии работы материала с касательным модулем деформации Е_t = d s/de < Е.

Н апряженно-деформированное

состояние центрально сжатого стержня: а — эпюра напряжений;

б — поперечное сечение стержня

Появляется дополнительный эксцентриситет а продольной силы. Приращение момента внешней силы d М_е = N(n + а). Для внутренних сил d М_i определится суммой соответствующих интегралов по площадям А₁ и А₂ разделенным нейтральной осью 2—2.

Тогда dМ_I = ρTJ, где Т представляет собой приведенный модуль деформации, определяемый из равенства TJ=EJ₁+E _T J₂. Откуда

Введение понятия приведенного модуля Т эквивалентно замене стержня из разнородного материала (участок А₁ подчиняется упругому закону, участок А₂ — пластическому) стержнем из однородного материала с уменьшенным модулем упругости.

Продолжая цепочку выкладок, напишем:

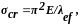
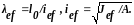
До сих пор рассматривался идеально прямой стержень с нагрузкой, приложенной строго по оси. В реальных конструкциях таких условий практически не существует. Ось стержня всегда имеет некоторые искривления, конструктивное оформление концов сжатых стержней не может обеспечить идеальную центровку сжимающей силы, что приводит к заметному снижению критических напряжений. Учет влияния указанных факторов осуществляется введением в расчет некоторого эквивалентного эксцентриситета сжимающей силы e_ef. Этот эксцентриситет зависит от многих случайных факторов: технологии изготовления, транспортировки, монтажа, конструктивного решения стержня и его узлов и т.д.

Статистические исследования эксцентриситетов показывают их зависимость от гибкости стержня — они возрастают с ростом гибкости. Поэтому в практических расчетах используют критическое напряжение, вычисленное с учетом случайных эксцентриситетов _cr,е.

Зависимость

критических

напряжений и

приведенного

модуля деформаций

от гибкости стержня:

1 — кривая Эйлера; 2 — кривая критических напряжений для сталей типа СтЗ; 3 — график модуля Т