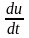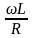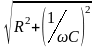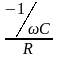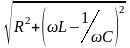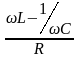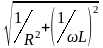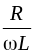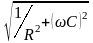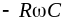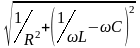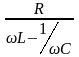- •1 Электрическая цепь
- •2 Мгновенная мощность и энергия
- •3 Сопротивление
- •4 Индуктивность
- •5 Емкость
- •6 Замещение физических устройств идеализированными элементами цепи
- •7 Источник эдс и источник тока
- •8 Законы кирхгофа
- •9 Электрическая цепь однофазного синусоидального тока гармонические колебания
- •10 Среднее и действующее значения функции
- •11 Представление гармонических колебаний в виде проекций вращающихся векторов
- •12 Гармонический ток в сопротивлении
- •13 Гармонический ток в индуктивности
- •14 Гармонический ток в емкости
- •15 16 Последовательное соединение r, l, с
- •17 Мощность в цепи гармонического тока
- •18 Применение комплексных чисел
- •19 Законы ома и кирхгофа в комплексной форме
- •20 Комплексная форма записи мощности
- •21. Цепи трехфазного тока. Независимая трехфазная цепь. Зависимая трехфазная цепь. Соединения звезда-звезда.
- •22. Цепи трехфазного тока. Соединения звездой и треугольником. Фазные и линейные токи и напряжения.
- •23. . Симметричный режим работы трехфазной цепи. Фазовый оператор. Соотношение между фазным и линейным токами и напряжениями в трехфазной цепи при соединении звезда-звезда. Векторная диаграмма.
- •24. . Симметричный режим работы трехфазной цепи. Фазовый оператор. Соотношение между фазным и линейным напряжениями в трехфазной цепи при соединении треугольник –треугольник. Векторная диаграмма.
- •26. Магнитные свойства вещества. Ферромагнитные материалы. Зависимость магнитной индукции от напряженности магнитного поля (петля Гистерезиса). Остаточная магнитная индукция. Коэрцитивная сила.
- •27. Явление электромагнитной индукции. Эдс электромагнитной индукции. Индуктивность, самоиндукция, взаимоиндуктивность.
- •28. Генератор постоянного тока. Устройство машины постоянного тока. Принцип действия.
- •30. Кпд и энергетическая диаграмма. Генератор постоянного тока.
- •31. Трансформатор. Устройство трансформатор. Режим холостого хода. Рабочий режим. Режим короткого замыкания
- •32. Электроника. Эффект Эдиссона. Электровакуумные приборы. Электровакуумный диод, его вольтамперные характеристики, применение в схемах выпрямления.
- •38. Электроника. Три схемы включения, транзисторы в схемах усиления.
- •39. Операционный усилитель, его обозначения и принцип действия.
- •46. Методы преобразования электрических схем. Эквивалетные преобразования звезды и треугольника резисторов.
17 Мощность в цепи гармонического тока
Ранее рассматривались энергетические соотношения в отдельных элементах R, L и С при гармоническом токе.
Разберем теперь более общий случай участка электрической цепи, напряжение на котором равно u = Umcosωt, а ток i = Imcos(ωt ).
Мгновенная мощность, поступающая в цепь,
p = UmImcostcos(ωt ) = UI[cos+cos(2ωt )]. (2.25)
состоит из двух слагающих: постоянной величины IUcos и гармонической, имеющей удвоенную частоту по сравнению с частотой напряжения и тока.
Среднее значение второй слагающей за время Т, в течение которого она совершает два цикла изменения, равно нулю. Поэтому средняя мощность, поступающая в рассматриваемый участок цепи,
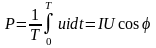 . (2.26)
. (2.26)
Множитель cos носит название коэффициента мощности.
Как видно из (2.26), активная мощность равна произведению действующих значений напряжения и тока, умноженному на коэффициент мощности.
Чем ближе угол к нулю, тем ближе cos к единице и, следовательно, тем меньше требуется величина тока I, при которой заданная средняя мощность Р при данном напряжении U будет передана от источника к приемнику.
Повышение коэффициента мощности промышленных электроустановок представляет важную технико-экономическую задачу.
Выражение средней мощности может быть преобразовано с учетом (2.18) и (2.23):
Р = zI2cos = RI2;
Р = yU2cos = gU2.
Активная мощность может быть также выражена через активную составляющую напряжения (Ua = Ucos) или тока (Iа = Icos):
P = UaI; P = UIa.
Рассмотрим более общий случай активно-реактивной цепи, например цепи, содержащей сопротивление и индуктивность; при этом
0 < < и 0 < cos< 1.
Согласно (2.25) мгновенная мощность колеблется с удвоенной угловой частотой 2 относительно линии, отстоящей от оси времени на P = UIcos (рисунок 2.22).
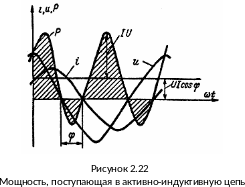
В промежутки времени, когда и и i имеют одинаковые знаки, мгновенная мощность положительна; энергия поступает от источника в приемник, преобразуясь в сопротивлении в тепло и запасаясь в магнитном поле индуктивности.
В промежутки времени, когда и и i имеют разные знаки, мгновенная мощность отрицательна и энергия частично возвращается приемником источнику. Как видно из рисунка 2.22, в течение большей части периода мгновенная мощность положительна и соответственно положительная (расположенная над осью времени) площадь кривой р преобладает над отрицательной площадью кривой р. В результате активная мощность Р > 0.
Аналогичная картина получается и в случае активно-емкостной цепи.
В электрических системах, в которых источниками электрической энергии являются генераторы переменного тока, мощность получается от первичных двигателей, приводящих генераторы во вращение. В радиотехнике и электронике, где гармонические колебания создаются с помощью электронных или полупроводниковых приборов, мощность получается от источников постоянного тока, питающих электронные генераторы или другого рода устройства.
Величина, равная произведению действующих значений тока и напряжения на зажимах цепи
S = UI, (2.27)
называется полной мощностью цепи и измеряется в вольт-амперах (ВА). Следует заметить, что амплитуда гармонической составляющей мгновенной мощности (2.25) численно равна полной мощности.
На основании (2.26) и (2.27) коэффициент мощности равен отношению активной мощности к полной:
cos
=
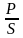 .
.
При расчетах электрических цепей и на практике в эксплуатации пользуются также понятием реактивная мощность, которая вычисляется по формуле Q = UIsin и является мерой потребления (или выработки) реактивного тока.
Эта мощность измеряется в реактивных вольт-амперах (вар).
Очевидно,
S2
= P2
+ Q2;
sin
=
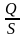 ;
tg
=
;
tg
=
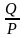 .
.
Выражение реактивной мощности может быть преобразовано с учетом (2.18) и (2.23):
Q = zI2sin = xI2;
Q = yI2sin = bU2.
Реактивная мощность может быть также выражена через реактивную составляющую тока (Iр = Isin) или напряжения (Up = Usin): Q = UIp; Q = UpI.
В соответствии с принятым ранее правилом знаков для угла реактивная мощность положительна при отстающем токе (индуктивная нагрузка) и отрицательна при опережающем токе (емкостная нагрузка) .
Понятия активная (средняя), реактивная и полная мощности являются удобными определениями мощностей, которые прочно укоренились на практике.
Реактивная мощность, подводимая к индуктивности, может быть представлена в следующем виде
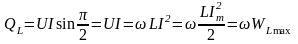 ,
,
где WLmax максимальное значение энергии, периодически запасаемой индуктивностью.
Реактивная мощность, подводимая к конденсатору, равна
QС
= Uisin(-
)
= -UI
= -ωCU2
= -ω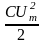 = -ωWCmax,
= -ωWCmax,
где WCmax – максимальное значение энергии, периодически запасаемой емкостью.
Реактивная мощность на зажимах цепи, содержащей индуктивность и емкость, пропорциональна разности максимальных значений энергии в магнитном и электрических полях:
Q = ω(WLmax WCmax). (2.28)
В таблице 2.1 дана сводка уравнений основных элементов цепи в общей форме (дифференциальной, интегральной) и при гармоническом режиме для мгновенных и действующих значений.
В таблице 2.2 приведены выражения полных сопротивлений и проводимостей цепи для различных сочетаний элементов R, L, C и соответствующие им значения tg.
Таблица 2.1 Уравнения основных элементов электрической цепи
Элемент |
Общая форма |
Гармонический режим |
|
мгновенные значения |
действующие значения |
||
Сопротивление
|
u = Ri i=gu |
u = RImcos(ωt+) i = gUmcos(ωt+) |
U = RI I = gU |
Индуктивность
|
u
=
L i
=
|
u = ωLImcos(ωt+) i
=
|
U = ωLI I
=
|
Ёмкость
|
u
=
i
=
C |
u = Imcos(ωt+) i=ωCUmcos(ωt++ ) |
U = I I = ωCU |
Таблица 2.2 Выражения для полных сопротивлений и проводимостей
Цепь |
Последовательное соединение |
|
Z |
tg |
|
R, L |
|
|
R, C |
|
|
R, L C |
|
|
Цепь |
Параллельное соединение |
|
Y |
tg |
|
R, L |
|
|
R, C |
|
|
R, L C |
|
|



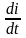
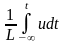
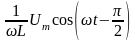
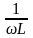 U
U