16.Пространственная когерентность. Роль конечных размеров источника.

Пространственная когерентность – когерентность света в направлении перпендикулярно лучу – это когерентность колебаний в один и тот же момент времени, но в разных точках плоскости (перпендикулярно направлению распространения цуга волны, где случайные изменения разности фаз между двумя точками увеличивается с увеличение расстояния между ними). Теряется, если разброс фаз достигает π. Длина простр. когерентности (радиус) r_когλ/φ -> длина волны

Источники должны быть пространственно когерентны, чтобы наблюдать разность фаз, интерференцию излучения или световых волн.

17.Опыт Юнга (с узкой и широкой щелью).

(график)

Интерференционные схемы. Во всех случаях световую волну, излучаемую одним источником делят на две части, а затем образовавшиеся волны накладывают друг на друга. Опыт Юнга основан на таком методе.

Щели Юнга: яркий свет проходит через щель S и вследствие дифракции (отклонение света от прямолинейной траектории) образует расходящуюся волну, которая падает на щели S₁ и S₂. Их можно рассматривать как вторичные источники света. В результате дифракции на S₁ и S₂ образуются 2 когерентные волны, которые накладываясь дают на экране Э интерференционные полосы. Ширина интерференционной полосы x = λ𝑙/d. Увеличение щелей приводит к уменьшению контрастности (видности) интерференционных полос.

18.Интерференция при отражении от тонких пластинок. Полосы равного наклона и полосы равной толщины. Кольца Ньютона.

Интерференция в тонких прозрачных пленках образуется в результате наложения когерентных волн, отражающихся от верхней и нижней поверхностей пленок.

(график1) и (график 2)

На фронте волны AD лучи имели одинаковую фазу, но затем прошли различные пути в разных средах и у них появилась разность хода Δ=(AB+BC)n-(DC+λ/2)=2ABn-DC-λ/2.

Из графика1 видно, что AB=BC=d/cos r, DC=ACsin i , AC=2dtg r и тогда

Воспользовавшись законом преломления света sin i=nsin r, перепишем выражение для разности хода

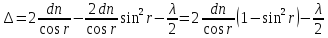
Так как cos r= = = 1/n окончательно имеем или (15.9).

В зависимости от величины D получится тот или иной результат интерференции. В отражённом свете условие максимума запишется так: (k=0, 1, 2, …) (15.10), а условие минимума, соответственно, так: (k=0, 1, 2, …) (15.11)

В монохроматическом свете плёнка будет видна либо освещенной, либо тёмной. Если на плёнку падает белый свет, то в результате интерференции волны какой-то определённой длины волны окажутся погашенными и плёнка будет окрашенной в дополнительный цвет к тому, что был уничтожен интерференцией.

Из условия максимума (15.10) и минимума (15.11) следует, что интерференционная картина в тонких плёнках зависит от n, l, d и i. Если плёнка (пластинка) однородна (n=const) и плоскопараллельна (d=const) и на неё падает монохроматический свет (λ=const) под разными углами (т.е. i ─ переменная величина), то в результате интерференции будут наблюдаться полосы равного наклона.

Полосы равной толщины наблюдаются, если угол падения лучей неизменный (i=const), а толщина пластины плавно изменяется. Если на пластинку падает белый свет, то полосы равной толщины будут иметь радужную окраску.

Примером полос равной толщины являются кольца Ньютона. Они образуются в результате интерференции лучей, отражённых от верхней и нижней поверхностей воздушного клина между линзой и пластинкой. Определим радиусы r тёмных и светлых колец Ньютона. Разность хода лучей в отражённом свете равна 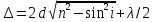(15.12) (перед λ/2 теперь берётся знак плюс, так как потеря полуволны имеет место при отражении на границе воздушной прослойки со стеклянной поверхностью нижней пластинки).

С учётом того, что показатель преломления воздуха n = 1 и при нормальном падении света i = 0, выражение для разности хода (15.13), где d ─ ширина воздушной прослойки. Приравняв (15.13) к условию максимума , получим(15.14)

Из графика2 видно, что R²=(R-d)²+r²=R²-2Rd+d²+r² откуда r²=2Rd.

Так как d<<R, d² можно пренебречь. Тогда радиус светлого кольца в отражённом свете

r² = (2k - 1)Rλ/2 или (k = 1, 2, 3, ...) (15.15)

Аналогично для тёмных колец с учётом условия минимума 2d + λ/2 = (2k + 1)λ/2, откуда

2d =2kλ/2 =kλ (15.16), а радиус тёмного кольца в отражённом свете r² = kλR или (k = 0, 1, 2, ...). (15.17) В отражённом свете в центре системы интерференционных колец всегда тёмное пятно, так как в точке касания линзы и пластинки из (15.13) D = λ/2 (условие минимума).