10.Волновое уравнение для электромагнитного поля в однородной изотропной среде (без вывода). Скорость электромагнитных волн. Показатель преломления.

Изотропная среда – та область пространства, физические свойства которой не зависят от направления. Электромагнитные волны – распространяемые в пространстве возмущения электромагнитного поля.

Есть провод с током -> «вихревое магнитное поле», ε_i=-dφ/dt - «вихревое электрическое поле». Меняем направление электрического поля Е – возникает магнитное поле => «электрическая волна». Индекс электрического поля D=ε₀εE; B=μ₀μH – индукция магнитного поля. (μ – относительная магнитная проницаемость, μ₀ - магнитная постоянная) Е перпендикулярно Н.

Волновое уравнение (без вывода)

[ ]

Скорость электромаг. волны: 1/v²==>v=1/

Скорость электромагнитных колебаний в вакууме: C=1/ ; скорость света в вакууме: v=C/; – показатель преломления среды.

11.Плотность энергии электромагнитной волны. Вектор Пойнтинга.

Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей w_e и w_m электрического и магнитного полей: w=w_e+w_m=ε₀εE²/2 + μ₀μH²/2

Так как 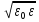*E=*H, то w=**E*H

Вектор S плотности потока энергии электромагнитной волны называется вектором Умова-Пойнтинга. S=[E*H] Вектор S направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную распространению волны.

12.Интенсивность электромагнитной волны.

Скалярная величина I, равная модулю среднего значения вектора Умова-Пойнтинга, называется интенсивностью волны: I=|S| (S-вектор)

Интенсивность волны численно равна энергии, переносимой волной за единицу времени сквозь единицу площади поверхности, нормальной к направлению распространения волны. Интенсивность волны пропорциональны квадрату ее амплитуды.

13.Световые лучи. Оптическая длина пути. Принцип Ферма. Закон отражения и преломления волны. Полное внутреннее отражение.

Оптика изучает природу света, световые явления, взаимодействие света с веществами. Свет: -мкм (длина волны). Оптическое излучение - электр. волны. Оптика: геометрическая (лучевая), волновая (физическая) и квантовая.Световые лучи - линии, перпендикулярные волновым поверхностям, вдоль которых распространяется свет. В однородной среде - прямая, при прохождении света, в неоднородной среде – искривленная (справедливо, пока λ << α).

Оптическая длина пути. В различных средах свет распространяется с разной скоростью. P=C/n (с - скорость распространения света в вакууме) n₁>n₂=>"1"=> оптически более плотная среда. n-показатель преломления среды. В однородной среде свет распространяется прямолинейно.

dt=dS/v -> t=; S_опт=(если среда однородна) => S_опт = nS, где S – расстояние, пройденное светом в среде с показ. преломл.

Принцип Ферма (основа геометрической оптики (λ<<α)). Свет распространяется таким образом, чтобы его оптическая длина была минимальна (т.е. минимальное время распространение)

Законы отражения и преломления волны.

(график 1)Закон отражения: отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела 2ух сред, а угол отражения равен углу падения. Q₁=Q₂

Закон преломление. (график 2) Луч падающий, луч преломляющийся и перпендикуляр лежат в одной плоскости и отношение sin угла падающего к sin угла преломления = const для данных сред.

sin θ₁/sin r=n₂/n₁ или sin θ₁n₁=sin rn₂

Полное внутреннее отражение. (график 3) Если свет распространяется из среды с большим n₂ (оптически более плотная) в среду с меньшим n₁ (n2>n1) (например из стекла в воздух), то угол преломления больше угла падения Q₁<Q₂ . Увеличивая угол падения при предельном угле θ_пред угол преломления окажется равным 90°, т.е. π/2 . При угле падения θ₁>θ_пред - свет полностью отражается, а при θ_пред -> полное внутренне отражение света.

n₁sinθ₁=n₂sin90°=n₂=>sinθ_пред=n₂/n₁ - угол полного внутреннего отражения света.