1.Колебательное движение. Гармоническая сила.Период колебаний.

Колебаниями называется точное или приближенное повторение какого-либо процесса с течением времени. Амплитудой гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия. Частотой колебаний называют число колебаний, совершаемых телом в 1 с. Величина w₀ (или просто w ) - это число колебаний тела, но не за 1 с., а за 2π . Она называется циклической или круговой частотой.

Колебания, не требующие подпитки энергией, называются свободными колебаниями. Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Если нет диссипативных сил, колебания происходят бесконечно долго (незатухающие колебания), если есть – затухающие колебания.

Свободные незатухающие колебания:

1)Консервативные силы

2)Наличие возвращающей силы, которая прямо пропорциональна смещению обобщающей координаты от положения равновесия. Эта силы называется гармонической силой

=> f(x) = E₁=(d²f/dx)|_x=x0*x²/2

d²f/dx|_x=x0 = k k>0 сила F=-γE/γx = -kx – гармоническая сила

x: x’’+w²x=0 - система способна выполнять гармонические колебания, если уравнение имеет решение.

x=C₁cos wt + C₂sin wt

x’= -wC₁sin wt + wC₂cos wt

x’’= -w²(C₁cos wt + C₂sin wt) = -w²x

x+w²x=0

Для получения решения дифференциального уравнения применим подходы:

1)Динамический (типа 2 закон Ньютона)

2)Энергетический (закон сохранения механической энергии)

Период колебаний - это промежуток времени, через который колебательная система совершит одно полное колебание. Период колебаний обозначается буквой T.

Одно полное колебание совершается, например, если груз, подвешенный на нити или на пружине, из положения А перейдет в положение В, а из него в положение А.Одно полное колебание совершается и в случае, если груз из положения О перейдет в положение А, затем - в положение В, а из него - в О.Если совершается N колебаний за промежуток времени t, то период колебаний равен: T=t/N. Таким образом, периодом колебания называют время, за которое совершается одно полное колебание.

2.Маятник. Уравнение гармонических колебаний.

(график 1)

F_x=-kx; a_x=x’’; F_x=ma_x; -kx=mx’’ mx’’+kx=0 x’’+(k/m)x=0 w²=k/m

w= T=2π/w=2π/;

x=Acos(wt + φ₀) – гармонические колебания

E=const; E=E_k+E_n; E_k=mv²/2=mv_x²/2=mx²/2; E_n=kx²/2;

mx²/2 + kx²/2 = const

x² + (k/m)x² = 2const/m = const’ – закон сохранения механической энергии

2*x’*x’’ + (k/m)*2*x’*x’’=0

x’’ + (k/m)x=0 => x’’ + w²x=0

(график 2)

Математический маятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести.

mg+T=ma; малые колебания => x

x: 0 + T sinα = mx’’; -Tα=mx’’

y: T cosα – mg=0; cosα 1 =>Tmg; -mgα=mx’’; x=α; x’’=𝑙α; -𝑔α=𝑙α’’; α’’𝑙 + gα=0; α’’ + (g/𝑙)α=0 => w==>T=2π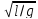

3.Энергия простого гармонического движения. Малые колебания.

x=Acos wt; E_к=mv²/2=mv_x²; v_x=x’=-Awsin wt; E_к=mA²w²/2*sin²wt; sin² wt=(1-cos² wt)

(графики)

Малые колебания.

Если система имеет минимальную потенциальную энергию, то малые колебания вблизи положения равновесия всегда будут гармоническими колебаниями.

4.Векторная диаграмма. Сложение параллельных колебаний. Биения.

(график 1)

Сложение параллельных колебаний. Биения.

x₁ = C₁ cos (w₁t + α₁); x₂ = C₂ cos (w₂t + α₂)

x=x₁ + x_2; x = C₁ cos (w₁t + α₁) + C₂ cos (w₂t + α₂)

Пусть C₁=C₂ и α₁= α₂=0

x = C cos(w₁t) + C cos(w₂t) = C (cos(w₁t) + cos(w₂t)) = 2C*cos (t(w₁+w₂)/2)* cos (t(w₁-w₂)/2)

Если |w₁-w₂| << w₁ => биение => x=2C*cos wt *cos Δwt/2 (Δw=w₁-w₂)

Пусть cos Δwt/2=A(t) => x=A(t) cos wt

Векторная диаграмма.

Одно колебание: x=Acos (wt +α₀)

t=0 => x=Acosα₀

(график 2)

Два колебания: x₁ -> r₁ x₁=Acos(w₁t)

x₂ -> r₂ x₂=Bcos(w₂t)

(график 3)

5.Сложение перпендикулярных колебаний. Фигуры Лиссажу.

1) w₁=w₂

α₁-α₂=π/2 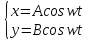x²/A² + y²/B² = 1 A=B=окружность

(график 1)

α₁=α₂ => Δα=0 => y=x*B/A

(график 2)

2) w₁/w₂ – рациональное число; w₁/w₂ = m/n

«Фигуры Лиссажу» - отношение числа касаний фигуры Лиссажу к границам прямоугольника равно отношению частот.

(график 3)

6.Уравнение затухающих колебаний. Декремент затухания. Логарифмический декремент затухания. Добротность.

(график 1)

Затухание за счет трения скольжения.

-kx = F_тр = mx’’; F_тр = μN = mg; mx’’ + kx = μmg|:m; x’’ + (k/m)x = μg; w²=k/m; w=

При затухающих колебаниях с учетом трения скольжения частота колебания не меняется, но меняется амплитуда μmg = kx => x=μmg/k – мин. Отношение, при кот. начинаются колебания.

В условиях трения скольжения колебательные процесс ограничен по времени.

Закон сохранения энергии. kA₀²/2 = μmg(A₀+A) + kA₁²/2; kA₁²/2 = μmg(A₁+A₂) = kA₂²/2 и т.д. (амплитуда все меньше и меньше)

(график 2)

Остановка процесса: A_n= μmg/k

Вязкое трение.

(график 3)

F_тр = -xv = -xx’, x – коэф. вязкого трения

Колебания в среде с вязким трением происходит бесконечно долго, а частота колебаний уменьшается.

Дифференциальное уравнение свободных затухающих колебаний.

(график 4)

d²s/dt² + 2δ(ds/dt) + w₀²s = 0, где s – колеблющ. велич., δ – коэф. затухания

В случае малых затуханий (δ²<< w₀²) решение этого уравнения: s=A₀e^-δtcos(wx+φ),

где A=A₀e^-δt – амплитуда затухающих колебаний, A₀ - начальная амплитуда, – циклическая частота затухающих колебаний.

T=2π/w’ = 2π/ – условно период затухающих колебаний.

Если A(t) и A(t+T) – амплитуды двух последовательный колебаний, соотв. моментам времени, отличающихся на период, то отношение A(t)/A(t+T)=e^δT называется декрементом затухания, а его логарифм θ = ln A(t)/A(t+T) = δT = T/t = 1/N называется логарифмическим декрементом затухания.

(N – число колебаний, соверш. за время уменьшения амплитуды в е раз.)

Добротностью колебательной системы называется безмерная величина Q, равнаяQ=π/λ