
1. Понятие о векторной и скалярной величинах. Величина, которая полностью характеризуется одним числовым значением, выражающим отношение этой величины к соответствующей единице измерения, называется скалярной величиной (скаляром). Величина,
которая кроме числового значения
характеризуется еще и направлением,
называется векторной величиной
(вектором). Определяется числом и
направлением. Обозначается
Вектор Ō, модуль, которого равен нулю, называется нулевым или нуль - вектором. Направление нулевого вектора произвольно. Два вектора считаются равными, если они расположены на параллельных или совпадающих прямых, имеют одинаковую длину и одинаково направлены. Существует свободный вектор, который допускает перенос в любую точку пространства, при условии сохранения длины и направления.
3. Понятие о базисных векторах. Расположение вектора по базисным векторам.
|
2 . Свойства и операции над векторами.
ax= | | * cosα ay= | | * cosβ az= | | * cosγ cosα2 + cosβ2 = 1 cosα2 + cosβ2 - cosγ = 1 совокупность проекций ay az вектор опр-ся однородностью сумма
векторов ищется по признаку парал-ма:
если векторы
и
Произведение
Скалярное
произведение любого вектора
(где Векторное произведение
-
вектор
ортогонален каждому
из векторов
и
- вектор
направлен
так, что тройка векторов
Обозначение:
Геометрически
векторное произведение Смешанное произведение Основная статья: Смешанное произведение
Сме́шанное
произведе́ние
|
4. Скалярное произведение 2-х векторов. (геом-е)
скалярное произведение
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними. Скалярное
произведение векторов
,
обозначается
символом Если
угол между векторами
,
обозначить
через
|
5 Свойства скалярного произведения. Свойства скалярного произведения. Для
любых векторов свойство
коммутативности скалярного
произведения свойство
дистрибутивности сочетательное
свойство скалярный
квадрат вектора всегда не отрицателен
|
6. Условия
коллинеарности и ортогональности
векторов. В
рассмотрении геометрических векторов
вводится определение следующей
операции.Произведением
вектора
|
7. Проекция одного вектора на другой. допустим вектора а(x1,y1) и b(x2,y2) Проекция=Косинус угла между векторами * |a| (длина проецируемого вектора) Косинус угла между векторами a и b = a*b/|a|*|b| скалярное произведение a*b=(x1*x2+y1*y2) длина векторов |a|=корень из(x1^2+y1^2); |b|=корень из(x2^2+y2^2);
8. Угол между векторами. Угол между векторами — угол между направлениями этих векторов (наименьший угол).
|
9. Векторное
произведение двух векторов. Векторным
произведением векторов
|
10. Свойства векторного произведения 2-х векторов
1)
Векторное произведение
равно
нулю, если векторы
и
коллинеарны
или какой-либо из перемножаемых
векторов является нулевым. 2) При
перестановке местами векторов
сомножителей векторное произведение
меняет знак на противоположный (см.
рисунок):
Выражение векторного произведения через проекции векторов и на координатные оси прямоугольной системы координат дается формулой
|
11. Геометрический смысл векторного произведения. По
определению длина векторного
произведения векторов равна
|
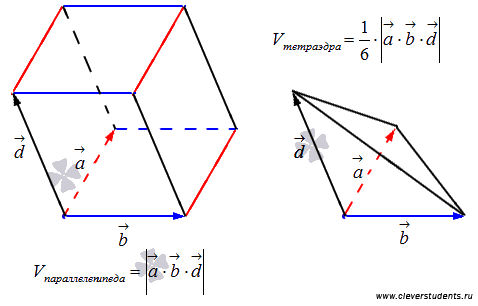
12. Смешанное произведение трех векторов Тройкой
векторов называются три вектора, если
указано, какой из них считается первым,
какой вторым и какой третьим. Тройку
векторов записывают в порядке нумерации;
например, запись
,
,
|
|
13.
Свойства смешанного произведения:
1)
|
14. Геометрический
смысл смешанного произведения.
Выясним геометрический смысл смешанного
произведения векторов
|
|
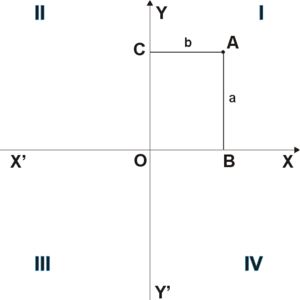
15. Прямоугольная
система координат
на плоскости образуется двумя взаимно
перпендикулярными осями координат
|
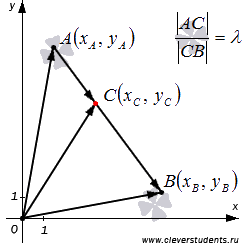
16. Деление
отрезка в заданном отношении.
Таким
образом, на плоскости координаты
точки С,
которая делит отрезок АВ
в отношении
,
находятся по формулам
|
|
17. Приведение квадратичной формы к каноническому виду. Метод Лагранжа — метод приведения квадратичной формы к каноническому виду Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть
есть данная квадратичная форма. Возможны два случая: хотя
бы один из коэффициентов все
коэффициенты В первом случае преобразуем квадратичную форму следующим образом:
С ней поступают аналогичным образом и так далее. Заметим,
что Второй
случай заменой переменных
19.
Уравнение прямой с угловым коэффициентом.
Уравнение
прямой вида
|
18.Общее уравнение
прямой на плоскости.Теорема.
Всякое уравнение
первой степени вида
|
|
20. Уравнение
прямой в отрезках.Уравнение
прямой вида
|
||
21. Каноническое уравнение прямой на плоскости : Если известны координаты точки A(x0, y0) лежащей на прямой и направляющего вектора n = {l; m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу:
(как дробь) Каноническое уравнение прямой в пространстве : Если известны координаты точки A(x0, y0, z0) лежащей на прямой и направляющего вектора n= {l;m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
|
22. Уравнение прямой, проходящей через две различные точки на плоскости Если прямая проходит через две точки A(x1, y1) и B(x2, y2), такие что x1 ≠ x2 и y1 ≠ y2 то уравнение прямой можно найти, используяследующую формулу
(как дробь) Уравнение прямой, проходящей через две различные точки в пространстве Если прямая проходит через две точки A(x1, y1, z1) и B(x2, y2, z2), такие что x1 ≠ x2, y1 ≠ y2 и z1 ≠z2 то уравнение прямой можно найти используя следующую формулу
|
|||||||||||||||||||||||||||||
23. Параметрическое уравнение прямой на плоскости: Параметрические уравнения прямой могут быть записаны следующим образом
где (x0, y0) - координаты точки лежащей на прямой, {l, m} - координаты направляющего вектора прямой. Параметрическое уравнение прямой в пространств: Параметрические уравнения прямой могут быть записаны следующим образом
где (x0, y0, z0) - координаты точки лежащей на прямой, {l; m; n} - координаты направляющего вектора прямой. |
24.
Расстояние от точки до прямой —
равно
длине перпендикуляра, опущенного из
точки на прямую.
Пример. Найти расстояние между прямой 3x + 4y -6 = 0 и точкой M(-1,3).Решение. Подставим в формулу коэффициенты прямой и координаты точки:
Ответ: расстояние от точки до прямой равно 0.6.
|
|||||||||||||||||||||||||||||
ax
=
ay
.
bx
by 25. Условие коллинеарности векторов Условия коллинеарности векторов : - Два вектора коллинеарные, если отношения их координат равны - Два вектора коллинеарные, если их векторное произведение равно нулю. Так в случае плоской задачи вектора a= {ax;ay}и b={bx;by}коллинеарны если: Условия ортогональности векторов. Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю: a· b= 0 Так в случае плоской задачи вектора a= {ax;ay}и b= {bx; by} ортогональны, если a· b= ax · bx + ay · by = 0
(остальное не нашла) |
26. Угол между двумя прямыми Угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k1x + b1 и y2 = k2x + b2, вычисляется по формуле:
Угол φ между двумя прямыми, заданными каноническими уравнениями (x-x1)/m1 = (y-y1)/n1 и (x-x2)/m2 = (y-y2)/n2, вычисляется по формуле:
Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида
|
|||||||||||||||
27.Общее
уравнение плоскости .частные
случаи.пределение. Плоскостью называется
поверхность, все точки которой
удовлетворяют общему
уравнению: Ax + By + Cz + D =
0
,где
А, В, С – координаты вектора -вектор нормали к
плоскости.
где Возможны следующие частные случаи : А = 0 – плоскость параллельна оси Ох, В = 0 – плоскость параллельна оси Оу С = 0 – плоскость параллельна оси Оz D = 0 – плоскость проходит через начало координат, А = В =0 – плоскость параллельна плоскости хОу А =С=0 –плоскость параллельна плоскости хОz В =С =0 –плоскость параллельна плоскости yOz А =D =0 – плоскость проходит через ось Ох В =D =0 – плоскость проходит через ось Оу С = D =0 – плоскость проходит через ось Oz А = В = D = 0 – плоскость совпадает с плоскостью хОу, А = С = D = 0 – плоскость совпадает с плоскостью xOz, В = С = D = 0 – плоскость совпадает с плоскостью yOz.
|
28. Уравнение плоскости в отрезках.
-
Если
в уравнении плоскости
(Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках
)
|
|||||||||||||||
29.
Пусть
в координатном пространстве
и
в качестве направляющих векторов плоскости, составим уравнение вида : которое называется уравнением плоскости, проходящей через три заданные точки.
|
30.Расстояние от точки до плоскости.
Пусть
плоскость
|
|||||||||||||||
|
|
31.Условие компланарности вектора и плоскости Пусть относительно общей декартовой системы координат в пространстве задана плоскость своим общим уравнением Ax+By+Cz+D=0. От произвольной точки M0 с координатами (x0, y0, z0) на плоскости α отложим вектор a={l, m, n}. Конец этого вектора - точка P (x0+l, y0+m, z0+n). Вектор a компланарен плоскости α тогда и только тогда, когда точка P принадлежит плоскости α, то есть координаты точки P удовлетворяют уравнению плоскости α. A(x0+l)+B(y0+m)+C(z0+n)+D=0. Последнее равенство перепишем в виде (Ax0+By0+Cz0+D)+(Al+Bm+Cn)=0. Выражение в первой скобке обращается в 0 тогда и только тогда, когда точка M0 принадлежит α, следовательно Al+Bm+Cn=0. Таким образом, установлено справедливое утверждение. Относительно общей декартовой системы координат, вектор a компланарен плоскости α (Ax+by+Cz+D=0) тогда и только тогда, когда Al+Bm+Cn=0.
![]() ,
(12)
,
(12)
![]() (13)
(13)
определяется по
аналогии с трехмерным случаем. А именно,
углом между плоскостями (12), (13) называется
угол ![]() между
векторами
между
векторами ![]() и
и ![]() ,
которые, как мы выяснили, перпендикулярны
к плоскостям (12) и (13) соответственно.
,
которые, как мы выяснили, перпендикулярны
к плоскостям (12) и (13) соответственно.
На основании формулы (8) § 6 имеем
 .
.
Плоскости (12) и (13)
перпендикулярны тогда и только тогда,
когда ![]() ,
т.е.
,
т.е.
![]() .
(14)
.
(14)
Две плоскости (12,
(13) параллельны тогда и только тогда,
когда перпендикулярные к ним
векторы ![]() и
и ![]() коллинеарны
коллинеарны ![]() ,
т. е. когда
,
т. е. когда
![]() .
(15)
.
(15)
Две плоскости пересекаются по прямой линии. Для построения линии их пересечения необходимо найти две точки, принадлежащие этой линии. Задача упрощается, если одна из пересекающихся плоскостей занимает частное положение. В этом случае ее вырожденная проекция включает в себя проекцию линии пересечения плоскостей.
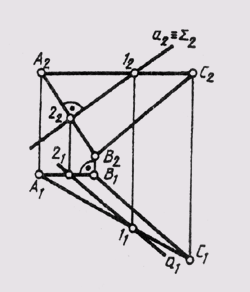
На рис. 122 приведен комплексный чертеж двух пересекающихся плоскостей £ и 0, причем плоскость Sum частного положения — фронтально проецирующая. Она пересекает линии АВ и АС плоскости 0, данной треугольниками ABC — плоскости общего положения. Точки пересечения 1 и 2 и определяют линию пересечения плоскостей. Соединив их, получаем искомую линию: a(1, 2) = Sum^Q.
Линию пересечения двух плоскостей, занимающих общее положение, можно построить в исходной системе плоскостей проекции. Для этого дважды решают задачу на построение прямой одной плоскости со второй плоскостью. Задачу можно решать в новой системе плоскостей проекции, построив изображение одной из пересекающихся плоскостей как плоскости проецирующей.
На рис. 123, а построена линия пересечения двух треугольников ABC и DEF путем построения точки М пересечения линии АВ с плоскостью DEF и точки N пересечения линии EF с плоскостью АВС:
1) АВ ~ Sum1(Sum1_|_П2), Sum1 ^DEF=l -2(12—22; 11—21), 11—21 ^ А1B1 = М1, M1,M2 || А1A2,М1М2 ^ А2В2 = М2,М(М,М2);
 рис
122.
рис
122.
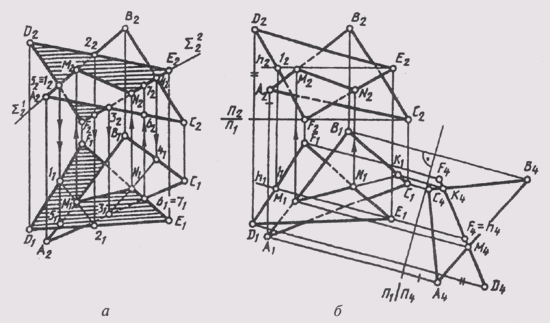
Рис. 123
2) EF ~ Sum2(Sum2_|_П2), Sum2 ^ ABC = 3—4(32—42; 31—41),31-41 ^ E1F1= = N1, N1N2 || A1,A2; N1N2^ E2F2 = N2; N(N1,N2);
3) M1 U N1, = M1N1, M2 U N2 = M2N2;
4) ABC^DEF = MN.
После построения определяют видимость пересекающихся плоскостей. На фронтальной плоскости она определена с помощью фронтально конкурирующих точек 1 и 5. Для определения видимости на горизонтальной плоскости проекций использованы горизонтально конкурирующие точки 6 и 7.
На рис. 123, б эта же линия пересечения построена с помощью дополнительных проекций данных плоскостей на плоскости П4, относительно которой плоскость DEFзанимает проецирующее положение. Дополнительные проекции построены из условия, что горизонталь h € DEF проецируется в точку на плоскости П4 _|_ h. Новые линии связи проведены .через незаменяемые горизонтальные проекции точек А,
В, С, D, E, F параллельно h1, а новая ось проекций П1/П4 _|_ h1. Замеренные на плоскости П2 высоты точек определили их проекции на плоскости П4.
A4B4C4^ D4E4F4 = M4K4, так как А4В4 ^ D4E4F4 = М4 и В4С4 ^ D4E4F4 = = К4. По направлению новых линий связи определяем горизонтальную проекцию линии МК (М1К1). Отмечаем точку пересечения стороны EF c линией МК: E1F1 ^ M1K1 = N1. Точки отрезка NK не имеют общих точек с плоскостью DEF.
Пересекающиеся плоскости в частном случае могут быть перпендикулярными. Для выявления случаев перпендикулярности надо помнить, что если две плоскости взаимно перпендикулярны, то одна из них проходит через перпендикуляр к другой плоскости. На рис. 122 дан комплексный чертеж взаимно перпендикулярных пересекающихся плоскостей: одна фронтально проецирующая Sum (Sum2), а вторая — общего положения (ABC) — содержит в себе перпендикуляр АВ к плоскости Sum(AB||П2; A2B2Sum2).
Две плоскости в общем случае могут пересекаться в бесконечности. Тогда имеет место параллельность этих плоскостей. При выявлении этого случая следует учитывать, что у параллельных плоскостей две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На рис. 91 плоскость S параллельна плоскости Sum2, так как а || с, b || d.
32. Угол между плоскостями.
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
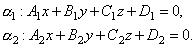

Под
углом между двумя плоскостями будем
понимать один из двугранных углов,
образованных этими плоскостями. Очевидно,
что угол между нормальными векторами
![]() и
и
![]() плоскостей α1 и α2 равен одному из
указанных смежных двугранных углов
плоскостей α1 и α2 равен одному из
указанных смежных двугранных углов
![]() или
или
![]() .Поэтому
.Поэтому
![]() .Т.к
.Т.к
![]() и
и
![]() ,то
,то
![]()
33. Общее уравнение прямой в пространстве.
Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.
Итак,
если уравнения двух непараллельных
плоскостей
![]() и
и
![]() , то прямая, являющаяся их линией
пересечения, задается системой уравнений
, то прямая, являющаяся их линией
пересечения, задается системой уравнений

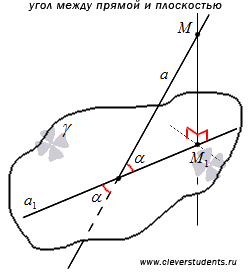
34. Угол между прямой и плоскостью.
Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией на плоскость.
Нахождение угла между прямой и плоскостью
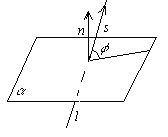
Пусть прямая и плоскость заданы уравнениями
![]()
Рассмотрим
векторы
![]() и
и
![]() .
.
Если
угол между векторами
и
острый,
то он будет
![]() ,
где φ
– угол между прямой и плоскостью. Тогда
,
где φ
– угол между прямой и плоскостью. Тогда
![]()
Если
угол между векторами
и
тупой
,то
он равен
![]()
Следовательно
![]() .
Поэтому в любом случае
.
Поэтому в любом случае
![]() .
.
Вспомнив формулу вычисления косинуса угла между векторами , получим
![]()
36.Общее и каноническое уравнение эллипса.
Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная.
Общее
уравнение эллипса
![]()
Каноническое
уравнение эллипса ![]() .
.
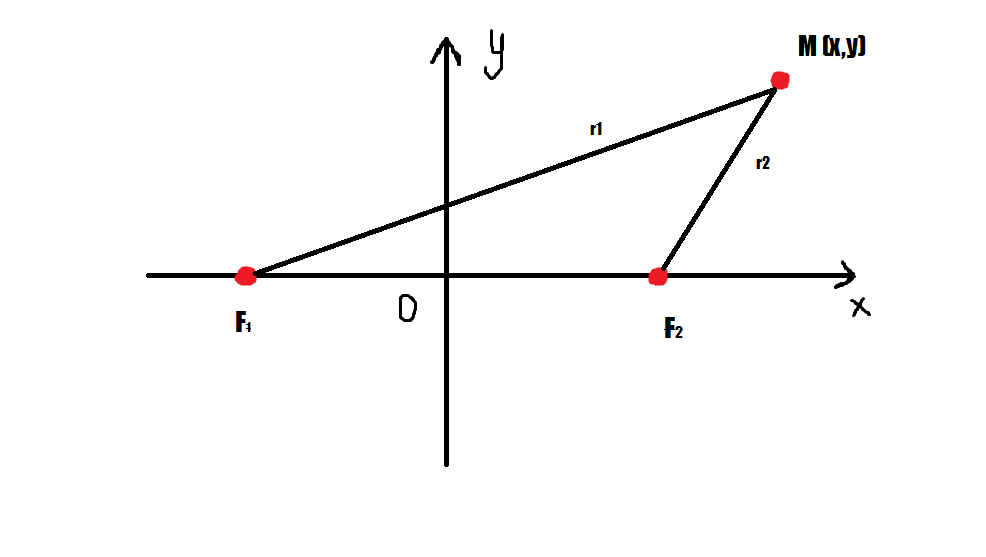
Доказательство.
При
совпадении точек F1
и
F2
эллипс
превращается в окружность. Выведем
уравнение эллипса, выбрав декартову
систему координат так, чтобы ось 0x
совпала с прямой F1
F2
,начало координат- с серединой отрезка
F1
F2.Пусть
длина этого отрезка равна 2c,
тогда в выбранной системе координат F1
(-с,0);
F2
(c,0).Пусть
точка M
(x,y)
лежит на эллипсе и сумма расстояний от
нее до F1
и F2
равна
2a.Тогда
r1 + r2 =
2a,но
![]() ,
,
![]() ,
откуда
получаем
,
откуда
получаем ![]()
Введя обозначение b2 = a2 – с2 и проведя несложные алгебраические преобразования получим каноническое уравнение эллипса
37.Основные свойства эллипса
Фокальное свойство эллипса
Точки ![]() ,
и
,
и ![]() называются
фокусами эллипса, расстояние между
ними
называются
фокусами эллипса, расстояние между
ними ![]() —
фокусным расстоянием, середина
—
фокусным расстоянием, середина ![]() отрезка
отрезка ![]() —
центром эллипса, число
—
центром эллипса, число ![]() —
длиной большой оси эллипса (соответственно,
число
—
длиной большой оси эллипса (соответственно,
число ![]() —
большой полуосью эллипса). Отрезки
—
большой полуосью эллипса). Отрезки ![]() и
и ![]() ,
соединяющие произвольную точку
,
соединяющие произвольную точку ![]() эллипса
с его фокусами, называются фокальными
радиусами точки
.
Отрезок, соединяющий две точки эллипса,
называется хордой эллипса.
эллипса
с его фокусами, называются фокальными
радиусами точки
.
Отрезок, соединяющий две точки эллипса,
называется хордой эллипса.
Отношение ![]() называется
эксцентриситетом эллипса. Из
определения
называется
эксцентриситетом эллипса. Из
определения ![]() следует,
что
следует,
что ![]() .
При
.
При ![]() ,
т.е. при
,
т.е. при ![]() ,
фокусы
и
,
а также центр
совпадают,
и эллипс является окружностью
радиуса
(рис.3.36,6).
,
фокусы
и
,
а также центр
совпадают,
и эллипс является окружностью
радиуса
(рис.3.36,6).
Геометрическое определение эллипса, выражающее его фокальное свойство, эквивалентно его аналитическому определению — линии, задаваемой каноническим уравнением эллипса:
![]()
Действительно,
введем прямоугольную систему координат
(рис.3.36,в). Центр
эллипса примем за начало системы
координат; прямую, проходящую через
фокусы (фокальную ось или первую ось
эллипса), примем за ось абсцисс
(положительное направление на ней от
точки
к точке
);
прямую, перпендикулярную фокальной оси
и проходящую через центр эллипса (вторую
ось эллипса), примем за ось ординат
(направление на оси ординат выбирается
так, чтобы прямоугольная система
координат
![]() оказалась правой
оказалась правой
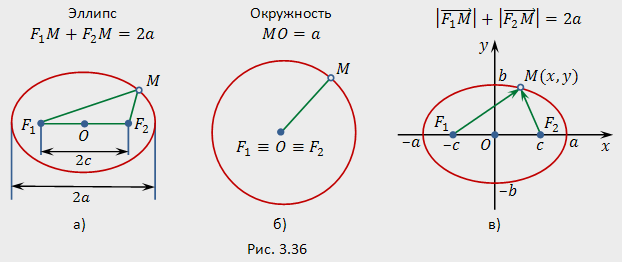
Составим
уравнение эллипса, пользуясь его
геометрическим определением, выражающим
фокальное свойство. В выбранной системе
координат определяем координаты фокусов
![]() .
Для произвольной точки
M (x
,y),
принадлежащей эллипсу, имеем:
.
Для произвольной точки
M (x
,y),
принадлежащей эллипсу, имеем:
![]()
Записывая это равенство в координатной форме, получаем:
![]()
Переносим второй радикал в правую часть, возводим обе части уравнения в квадрат и приводим подобные члены:
![]()
Разделив на 4, возводим обе части уравнения в квадрат
![]()
Обозначив
![]() , получаем
, получаем
![]() .
Разделив
обе части на
.
Разделив
обе части на
![]() , приходим к каноническому уравнению
эллипса:
, приходим к каноническому уравнению
эллипса:
Следовательно, выбранная система координат является канонической.
Если
фокусы эллипса совпадают, то эллипс
представляет собой окружность
(рис.3.36,6), поскольку
![]() .
В этом случае канонической будет любая
прямоугольная система координат с
началом в точке
.
В этом случае канонической будет любая
прямоугольная система координат с
началом в точке
![]() ,
а уравнение
,
а уравнение
![]() является уравнением окружности с центром
в точке О и радиусом, равным a.
является уравнением окружности с центром
в точке О и радиусом, равным a.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.49), и только они, принадлежат геометрическому месту точек, называемому эллипсом. Другими словами, аналитическое определение эллипса эквивалентно его геометрическому определению, выражающему фокальное свойство эллипса.
Директальное свойство эллипса.
Директрисами
эллипса называются две прямые, проходящие
параллельно оси ординат канонической
системы координат на одинаковом
расстоянии
![]() от нее.При
,
когда эллипс является окружностью,
директрис нет (можно считать, что
директрисы бесконечно удалены).
когда
эллипс является окружностью, директрис
нет (можно считать, что директрисы
бесконечно удалены).
от нее.При
,
когда эллипс является окружностью,
директрис нет (можно считать, что
директрисы бесконечно удалены).
когда
эллипс является окружностью, директрис
нет (можно считать, что директрисы
бесконечно удалены).
Эллипс
с эксцентриситетом
![]() можно определить, как геометрическое
место точек плоскости, для каждой из
которых отношение расстояния до заданной
точки
можно определить, как геометрическое
место точек плоскости, для каждой из
которых отношение расстояния до заданной
точки
![]() (фокуса) к расстоянию до заданной прямой
(фокуса) к расстоянию до заданной прямой
![]() (директрисы), не проходящей через заданную
точку, постоянно и равно эксцентриситету
(директрисы), не проходящей через заданную
точку, постоянно и равно эксцентриситету
![]() директориальное свойство эллипса).
Здесь
и
— один из фокусов эллипса и одна из его
директрис, расположенные по одну сторону
от оси ординат канонической системы
координат, т.е.
директориальное свойство эллипса).
Здесь
и
— один из фокусов эллипса и одна из его
директрис, расположенные по одну сторону
от оси ординат канонической системы
координат, т.е.
![]() или
или
![]()
В самом
деле, например, для фокуса
и директрисы
![]() (рис.3.37,6) условие
(рис.3.37,6) условие
![]() можно записать в координатной форме
можно записать в координатной форме
![]()
Избавляясь
от иррациональности и заменяя
![]() ,
приходим к каноническому уравнению
эллипса (3.49). Аналогичные рассуждения
можно провести для фокуса
и директрисы
,
приходим к каноническому уравнению
эллипса (3.49). Аналогичные рассуждения
можно провести для фокуса
и директрисы
![]()

38.


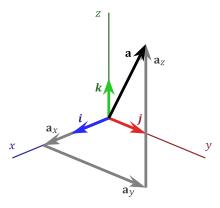 Разложение
вектора по трём ортогональным векторам
трёхмерного евклидова пространства
Векторы (как направленные отрезки),
лежащие на прямых, параллельных одной
прямой, называются коллинеарными,
а векторы, лежащие в плоскостях,
параллельных однойплоскости — компланарными.
Для свободных векторов коллинеарность
и компланарность определяется как
такие понятия для изображающих их
направленных отрезков (то есть
представителей соответствующих
свободным векторам классов
эквивалентности). Каждый вектор
плоскости можно единственным образом
разложить по двум определённым
неколлинеарным векторам этой плоскости,
а каждый вектор трёхмерного евклидова
пространства можно единственным
образом разложить по трём определённым
некомпланарным векторам. Эти векторы,
взятые в определённом порядке называются
базисом плоскости (пространства).
Сопоставлением каждому вектору данной
плоскости (пространства) его коэффициентов
в таком его разложении, определяется аффинная
система координатна
плоскости (в пространстве). Если
векторы, по которым производится
разложение, ортогональны и единичны,
то получаем прямоугольную
декартову систему координат на
плоскости (в пространстве). Разложение
геометрического вектора по базису
есть упорядоченная совокупность
проекций вектора на базисные вектора.
Разложение
вектора по трём ортогональным векторам
трёхмерного евклидова пространства
Векторы (как направленные отрезки),
лежащие на прямых, параллельных одной
прямой, называются коллинеарными,
а векторы, лежащие в плоскостях,
параллельных однойплоскости — компланарными.
Для свободных векторов коллинеарность
и компланарность определяется как
такие понятия для изображающих их
направленных отрезков (то есть
представителей соответствующих
свободным векторам классов
эквивалентности). Каждый вектор
плоскости можно единственным образом
разложить по двум определённым
неколлинеарным векторам этой плоскости,
а каждый вектор трёхмерного евклидова
пространства можно единственным
образом разложить по трём определённым
некомпланарным векторам. Эти векторы,
взятые в определённом порядке называются
базисом плоскости (пространства).
Сопоставлением каждому вектору данной
плоскости (пространства) его коэффициентов
в таком его разложении, определяется аффинная
система координатна
плоскости (в пространстве). Если
векторы, по которым производится
разложение, ортогональны и единичны,
то получаем прямоугольную
декартову систему координат на
плоскости (в пространстве). Разложение
геометрического вектора по базису
есть упорядоченная совокупность
проекций вектора на базисные вектора.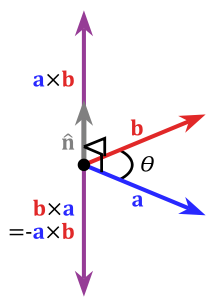 Векторным
произведением вектора
на
вектор
называется
вектор
Векторным
произведением вектора
на
вектор
называется
вектор 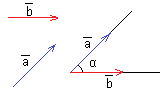 По
определению, угол
между двумя векторами находится в
промежутке [0°;
180°].
Угол
между векторами
По
определению, угол
между двумя векторами находится в
промежутке [0°;
180°].
Угол
между векторами 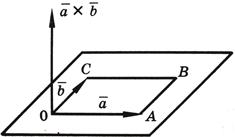 Векторное
произведение векторов
и
обозначается
символом
Векторное
произведение векторов
и
обозначается
символом 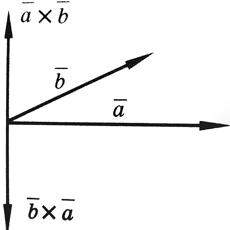 3)
3) 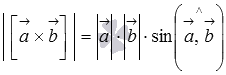 .
А из курса геометрии средней школы
нам известно, что площадь треугольника
равна половине произведения длин двух
сторон треугольника на синус угла
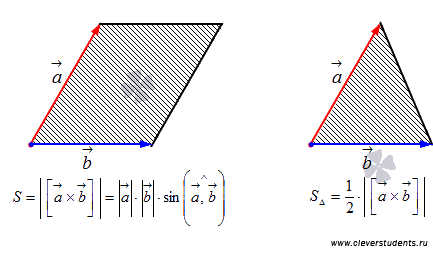
между ними. Следовательно, длина
векторного произведения равна удвоенной
площади треугольника, имеющего
сторонами векторы
.
А из курса геометрии средней школы
нам известно, что площадь треугольника
равна половине произведения длин двух
сторон треугольника на синус угла
между ними. Следовательно, длина
векторного произведения равна удвоенной
площади треугольника, имеющего
сторонами векторы
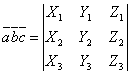 .
.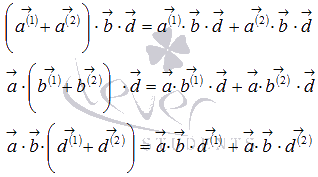 Очевидно,
что если хотя бы один из умножаемых
векторов нулевой, то смешанное
произведение равно нулю. Смешанное
произведение также равно нулю, если
хотя бы два умножаемых вектора равны.
Действительно, если
Очевидно,
что если хотя бы один из умножаемых
векторов нулевой, то смешанное
произведение равно нулю. Смешанное
произведение также равно нулю, если
хотя бы два умножаемых вектора равны.
Действительно, если
 Положение точки
Положение точки
 Мы
знаем, что координаты
радиус-вектора
точки равны соответствующим координатам
этой точки, поэтому,
Мы
знаем, что координаты
радиус-вектора
точки равны соответствующим координатам
этой точки, поэтому,
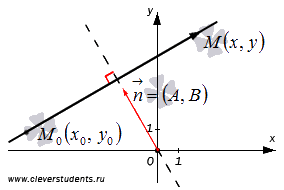 Таким
образом, уравнение
задает
прямую линию в прямоугольной декартовой
системе координат Oxy
на плоскости, следовательно, эквивалентное
ему уравнение вида
задает
эту же прямую. На этом первая часть
теоремы доказана. Теперь докажем, что
всякая прямая в прямоугольной системе
координат Oxy
на плоскости определяется уравнением
первой степени вида
.
Пусть в прямоугольной системе координат
Oxy
на плоскости задана прямая a,
проходящая через точку
,
-
нормальный
вектор прямой
a,
и пусть
-
плавающая точка этой прямой. Тогда
векторы
и
перпендикулярны,
следовательно, их скалярное
произведение
равно нулю, то есть,
Таким
образом, уравнение
задает
прямую линию в прямоугольной декартовой
системе координат Oxy
на плоскости, следовательно, эквивалентное
ему уравнение вида
задает
эту же прямую. На этом первая часть
теоремы доказана. Теперь докажем, что
всякая прямая в прямоугольной системе
координат Oxy
на плоскости определяется уравнением
первой степени вида
.
Пусть в прямоугольной системе координат
Oxy
на плоскости задана прямая a,
проходящая через точку
,
-
нормальный
вектор прямой
a,
и пусть
-
плавающая точка этой прямой. Тогда
векторы
и
перпендикулярны,
следовательно, их скалярное
произведение
равно нулю, то есть,
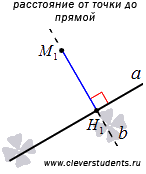 Если точка лежит на прямой, то расстояние
от точки до прямой считается равным
нулю. Если задано уравнение прямой
Ax+ By+ C = 0, то расстояние от точки M(Mx,
My)
до прямой можно найти, используя
следующую формулу:
Если точка лежит на прямой, то расстояние
от точки до прямой считается равным
нулю. Если задано уравнение прямой
Ax+ By+ C = 0, то расстояние от точки M(Mx,
My)
до прямой можно найти, используя
следующую формулу: Как
показано точка
Как
показано точка  Используя
векторы
Используя
векторы Вектор
Вектор