Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Инженерно-строительный институт

институт

ИСЗиС

кафедра

Отчет по лабораторной работе по дисциплине «Гидравлика»

Изучение физических свойств жидкости

тема

Преподаватель					Кропоткин Б.И.
			подпись, дата		инициалы, фамилия

Студент,	АФ 10-21				Соломкина Е.А.
	номер группы		подпись, дата		инициалы, фамилия

Рейм Н.Ю.

Клиняева А.С.

Мамонтова А.М.

Красноярск 2012.

Содержание:

1. Введение ………………...…………………………….…………..……………….…… 3

1.1. Основные физические характеристики …………….………………………………….. 3

1.2. Модели жидкости ………………………………………….……………………………. 5

1.3.Взаимодействие жидкостей и газов…………………………………………….………...6

1.4. Силы, действующие на жидкость ……………………………….……………………... 7

2. Работа №1. Определение динамической вязкости жидкости ...……………….…….. 8

3. Работа №2. Определение температурного коэффициента объёмного расширения жидкости …………………...................................................................................................... 10

4. Работа №3. Определение плотности жидкости …….............................................…. 12

5. Работа №4. Определение коэффициента поверхностного натяжения жидкости …13

Список использованных источников ………………………………...…………………..... 14

Введение

Гидравлика является самостоятельным разделом механики, изучает законы равновесия и движения сплошных сред (жидкости), обладающих свойством текучести, а также механическое взаимодействие этих сред с твердыми телами. К таким средам (физическим телам) относятся все жидкости, то есть капельные жидкости и газы.

Капельная жидкость ̶ молекулы плотно прилипают друг к другу и образуют каплю.

̶ Молекулы на поверхности капли притягиваются и образуют каплю;

̶ Молекулы поверхностного слоя сжимают жидкость внутри капли.

1. Основные физические характеристики:

1. Плотность р (кг/м³) ̶ это количество вещества, содержащегося в единице объёма.

р = m/V

Плотность газов существенно зависит от температуры и давления, а у капельной жидкости она практически не меняется при колебании внешних условий.

2. Удельный вес γ (Н/м³) ̶ это сила, с которой количество вещества р притягивается к Земле, то есть сила тяжести.

γ = pg

где g ̶ ускорение свободного падения (g = 9,81 м/с²).

3. Сжимаемость ̶ способность жидкости изменять свой объём под действием приложенной к ней силы. Сжимаемость тела под давлением р характеризуется коэффициентом объёмного сжатия β (м²/Н), а величина, обратная коэффициенту β ̶ это модуль упругости Е (Па):

β = 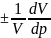; Е =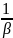

Капельная жидкость ̶ не сжимается.

4. Расширение ̶ изменение объёма тела при изменении его температуры Т, определяется температурным коэффициентом объемного расширения βт (1/К):

β =

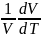
Перечисленные параметры являются общими для всех жидких и твёрдых тел. Но есть специфические свойства, присущие только жидкостям /1 ̶ 4/.

При этом следует иметь в виду, что к жидкостям в широком смысле этого слова относятся и капельные жидкости, и газы, так как они в основном подчи­няются одним и тем же физическим законам (за редкими исключениями).

Например, плотность капельной жидкости практически не меняется при колебании температуры и давления, а у газов она существенно зависит от внешних условий.

5. Текучесть ̶ это способность жидкости неограниченно деформироваться

под действием приложенной силы, так как капельная жидкость и газ в состоя­нии покоя не воспринимают касательных напряжений.

6. Вязкостью называется способность жидкой среды при движении сопротивляться сдвигу.

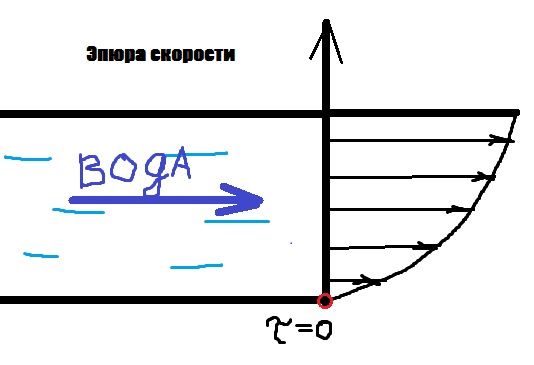В потоке жидкости, движущем­ся по направлению горизонтальной оси х, в поперечном сечении (например, по оси у) скорости 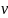распределены неравномерно, т.е. наблюдается относитель­ное смещение смежных слоев. Следовательно, происходят деформации сдвига и возникают касательные напряжения (τ). Это явление описал Ньютон, он же сформулировал закон вязкостного трения жидкости:

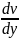τ = µ (1)

где коэффициент пропорциональности µ ̶ это характеристика жидкости, называемая динамической вязкостью, Па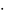 с.

=>

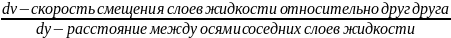поперечный градиент скорости. Эпюра скоростей показывает распределение скоростей в потоке.

Из выражения видно, что динамическая вяз­кость численно равна единичной силе трения τ при градиенте скорости между отдельными слоями потока равном единице. Знак в формуле (1) гово­рит о том, что два соседних слоя жидкости взаимодействуют друг с другом: один слой, движущийся с большей скоростью, уско­ряет другой ̶ знак плюс, а этот другой тормозит первый ̶ знак минус.

Кроме обычных (ньютоновских) жидкостей, для которых ха­рактерно уравнение (1), существуют еще аномальные (ненью­тоновские) жидкости. Для таких жидкостей за­кон внутреннего трения выражается в виде

τ = 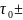µ

где ̶ касательные напряжения в покоящейся жидкости, после преодоления, которых жидкость приходит в движение.

Вязкость зависит от температуры: в капельных жидкостях повышение температуры приводит к уменьшению вязкости, а в газах ̶ наоборот.

Кинематическая вязкость (м²/с) связана с динамической соотноше­нием

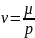(2)

7. Свободная поверхность капельной жидкости силами молекулярного взаимодействия стягивается до минимума; последние характеризуются коэффициентом поверхностного натяжения Ɠ (Н/м).

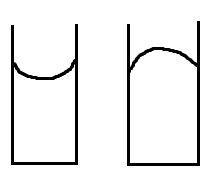Поверхностное натяжение измеряется силой, приходящейся на единицу длины (периметра), а общая сила поверхностного натяжения вычисляется по формуле

F_п = Ɠl,

где Ɠ ̶ единичная сила или коэффициент поверхностного натяжения, Н/м²; l ̶ длина или периметр действия силы, м.

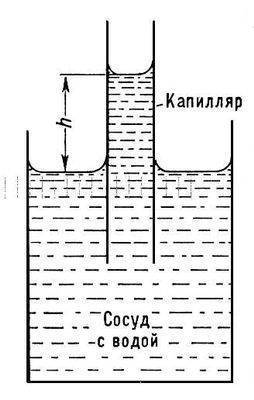В месте со­прикосновения с твердым телом свободная поверхность искривляется: если те­ло не смачивается жидкостью, то появляется выпуклый мениск, если смачива­ется ̶ вогнутый. В движущемся потоке жидкости непосредственно у смочен­ной поверхности русла скорость равна нулю, так как пограничный слой жидко­сти прилипает к ней и в движении не участвует.

Например: Если взаимосвязь молекул жидкости между собой больше чем взаимосвязь между стенками сосуда, то мениск выпуклый. И наоборот. Образуются мениски ̶ вогнутые или выпуклые поверхность жидкости в узкой трубке. В случае вогнутой поверхности жидкости (r < 0) давление в ней понижено по сравнению с давлением в соседней фазе: p1< p2 . Для выпуклых поверхностей (r > 0) давление повышено. Капиллярное давление создаётся силами поверхностного натяжения, действующими по касательной к поверхности раздела.