Гидравлический удар в трубах

Гидравлический удар представляет собой колебательный про­цесс, возникающий в упругом трубопроводе с малосжимаемой жид­костью при внезапном изменении ее скорости или давления. Этот процесс является очень быстротечным и характеризуется чередо­ванием резких повышений и понижений давления. Изменение дав­ления при этом тесно связано с упругими деформациями жидкости и стенок трубопровода.

Гидравлический удар чаще всего возникает вследствие быстро­го закрывания или открывания крана или другого устройства управления потоком. Но могут быть и другие причины его возник­новения.

Пусть в конце трубы, по которой движется жидкость произведено мгновенное закрывание крана А (рис. 126, а). Тогда скорость частиц жидкости, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в ра­боту деформаций стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с повыше­нием давления. На заторможенные частицы у крана набе­гают другие, соседние с ними частицы, и тоже теряют скорость, в результате чего сечение n-n передвигается вправо со скоростью a, называемой скоростью ударной волны; сама же переходная об­ласть, в которой давление изменяется на величину р_уд, называет­ся ударной волной.

Когда ударная волна добежит до резервуара, жидкость ока­жется остановленной и сжатой во всей трубе, а стенки ее — растянутыми. Ударное повышение давления р_уд распространится: на всю трубу (рис. 126,б).

Но такое состояние не является равновесным. Под действием перепада давлений р_уд жидкость устремится из трубы в резерву­ар, причем это движение начнется с сечения, непосредственно при­легающего к резервуару. Сечение n-n побежит теперь обратно к крану со скоростью а, оставляя за собой выравненное давление р_о (рис. 126, б).

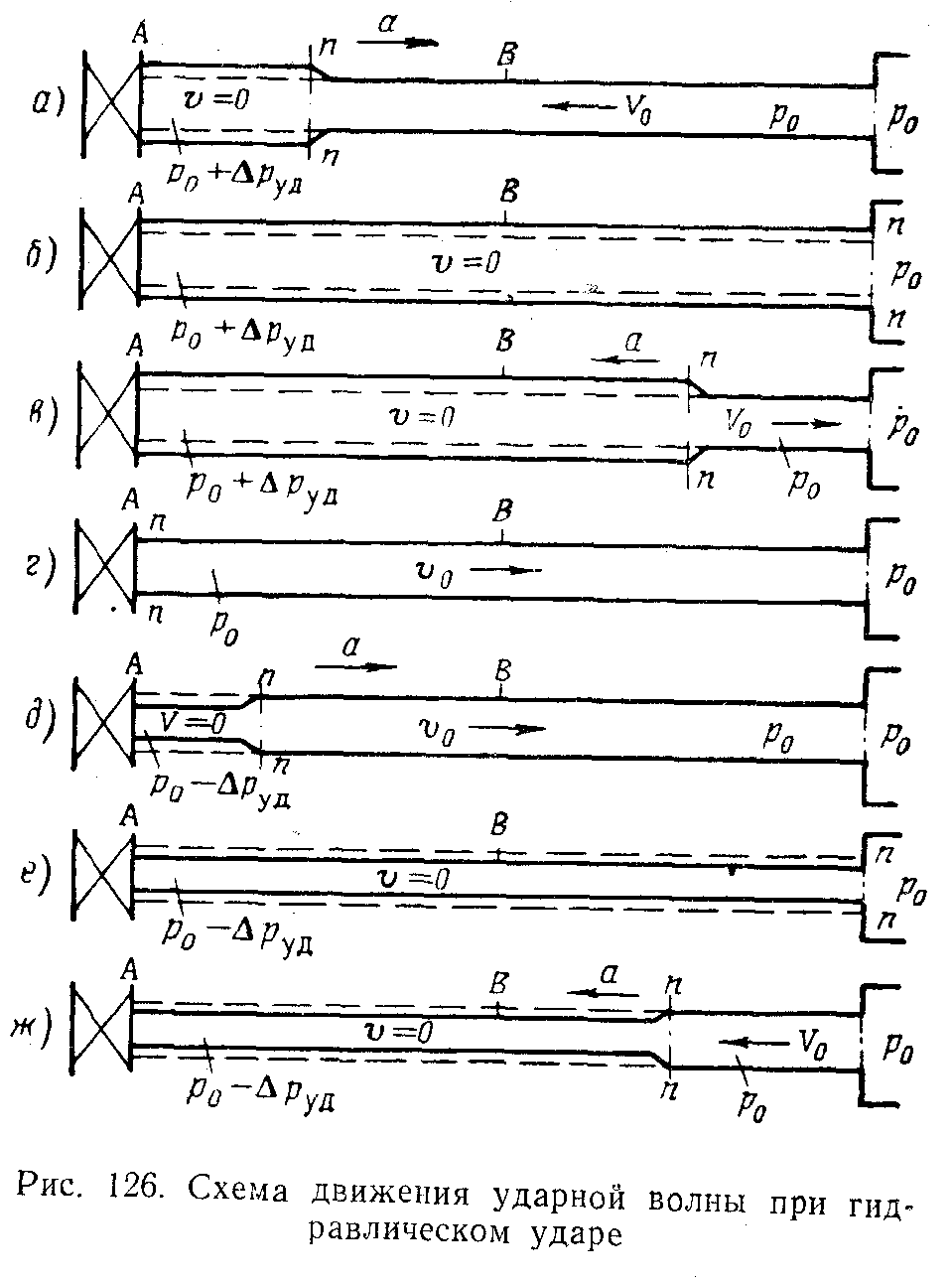
Жидкость и стенки трубы предполагаются совершенно упруги­ми, поэтому они возвращаются к прежнему состоянию, соответст­вующему давлению р_о. Работа деформаций полностью переходит обратно в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость _о, но направленную теперь в противопо­ложную сторону.

С этой скоростью жидкая колонна (рис. 126, г) стремится ото­рваться от крана, вследствие чего возникает отрицательная удар­ная волна — р_уд, которая бежит от крана к резервуару со ско­ростью а, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления—р_уд (рис. 126, д). Кинетическая энергия жидкости вновь переходит в ра­боту деформаций, но противоположного знака.

Состояние трубы в момент прихода отрицательной ударной вол­ны к резервуару показано на рис. 126, е. Так же, как и для случая, показанного на рис. 126,б, оно не является равновесным. На рис. 126, ж показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся образованием скорости _о.

Очевидно, что как только отраженная от резервуара ударная волна достигнет крана, возникнет ситуация, уже имевшая место в момент закрывания крана. Весь цикл гидравлического удара повторится снова.

Формула Н. Е. Жуков­ского для определения р_уд:

Скорость распространения ударной волны:

или

В том случае, когда уменьшение скорости в трубе происходит не до нуля, а до значения , возникает так называемый неполный гидравлический удар и формула Н.Е. Жуковского приобретает вид:

Эта формула справедлива при очень быстром закрывании кра­на или, точнее говоря, когда время закрывания

где время t_o называется фазой гидравлического удара.

При этом условии имеет место прямой гидравлический удар При более медленном закрывании возникает так называемый непрямой гидравлический удар, при котором ударная волна, отразившись oт резер­вуара, возвращается к крану раньше, чем он будет полностью за­крыт. Очевидно, что повышение давления р’_уд при этом будет меньше, чем при прямом ударе:

Таким образом величина р’_уд в отличие от р_уд зависит от длины трубы, но не зависит от скорости а.

Следует иметь в виду, что в так называемом тупиковом тру­бопроводе возможно увеличение ударного давления в два раза.

Если в конце трубопровода имеется объем W, заполненный жид­костью, например, силовой гидроцилиндр, то этот объем оказывает демпфирующее действие и давление повышается меньше, чем в два раза. При весьма большом объеме W отражения волны практиче­ски не происходит.

В результате специальных исследований гидравлического уда­ра в трубопроводах самолетных гидросистем выяснилось, что в реальных условиях при достаточно высоких начальных давлениях р_о величина р_уд на 10—20% и более превосходит теоретическое значение по фор­муле Н.Е. Жуковскому. Объясняется это тем, что с ростом дав­ления р_о несколько возрастает модуль упругости жидкости К, а следовательно, растет и скорость а. Это означает, что про­исходит некоторое отклонение от закона Гука, т. е. нарушение линейности изменения деформаций по давлению.

Благодаря быстродействию устройств управления гидросистем (электромагнитных кранов и др.), время срабатывания которых чрезвычайно мало (порядка 0,008—0,002 се/с), величина р_уд в на­порных линиях самолетных гидросистем достигает нескольких де­сятков и даже сотен кГ/см². Эти резкие повышения давления могут выводить из строя отдельные агрегаты и трубопроводы. Кроме того, импульсы давления при гидравлическом ударе, распространяю­щиеся по всей системе трубопроводов, могут быть причиной неожи­данных срабатываний отдельных устройств системы (реле давле­ния, гидрозамков и т. п.).

Способы борьбы с гидравлическим ударом в са­молетных системах выбираются для каждого конкретного случая. Наиболее эффективным методом снижения р’_уд является устране­ние возможности прямого гидравлического удара, что при задан­ном трубопроводе сводится к увеличению времени срабатывания кранов и др. устройств. Аналогичный эффект достигается установ­кой перед этими устройствами компенсаторов в виде достаточных местных объемов жидкости или гидроаккумуляторов. Уменьшение скорости движения жидкости в трубопроводах (увеличение диа­метра труб при заданном расходе) и уменьшение длины трубо­проводов (для получения не прямого удара) также способствует снижению ударного давления. Иногда уменьшению давления р’_уд предпочитают повышение прочности слабых звеньев, системы.

ОТНОСИТЕЛЬНОЕ И НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЖИДКОСТИ В ТРУБАХ

УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ ДВИЖЕНИЕ В УСЛОВИЯХ НЕВЕСОМОСТИ

Уравнение Бернулли справед­ливо в тех случаях установившегося течения жидкости, когда из числа массовых сил на жидкость действует лишь сила тяжести. Однако в авиационной и ракетной технике приходится сталкивать­ся с такими течениями, при расчете которых, помимо силы тяже­сти, нужно учитывать еще и силы инерции переносного движения. Это будет в тех случаях, когда русло (например, трубопровод), по которому движется жидкость, само перемещается в пространст­ве с тем или иным ускорением. Если возникающая при этом инер­ционная сила постоянна по времени, то течение жидкости относи­тельно стенок русла может быть установившимся, и для него мож­но вывести уравнение Бернулли. Различие будет заключаться в том, что к работе сил давления и сил тяжести нужно добавить еще работу силы инерции. Уравнением Бернулли для отно­сительного движения имеет вид:

где H_ин — так называемый инерционный напор, который пред­ставляет собой работу силы инерции, отнесенную к единице веса и взятую с обратным знаком.

Прямолинейное равноускоренное движение русла. Если рус­ло, по которому течет жидкость, движется прямолинейно с посто­янным ускорением а, то в этом случае 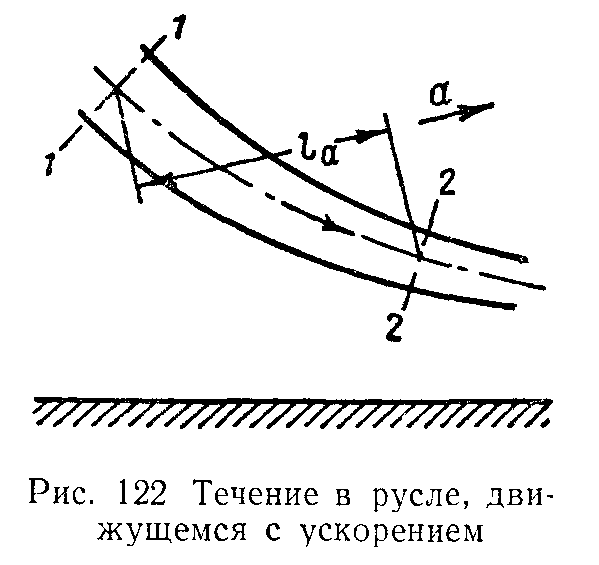(рис. 122) на все частицы жидкости, движущейся по данному руслу, действует одинаковая и постоянная по времени сила инерции переносного движения, ко­торая может способствовать или препятствовать течению:

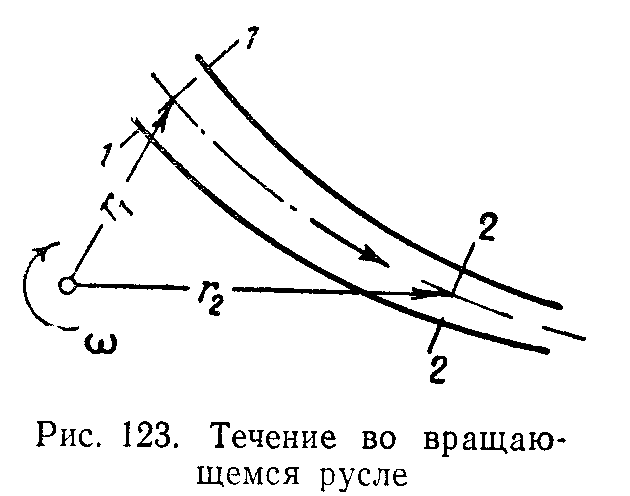В ращение русла вокруг вертикальной оси. Пусть русло, по которому движется жидкость, вращается вокруг вертикальной оси с постоянной угловой скоростью (рис. 123). Тогда на жидкость будет действовать сила инерции вращательного движения, являю­щаяся функцией радиуса:

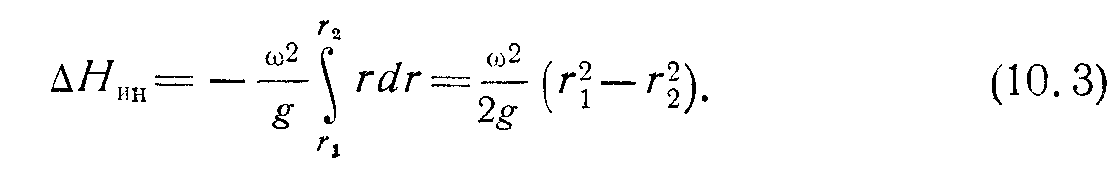
Движение жидкости в условиях невесомости характеризуется прежде всего тем, что результирующая массовая сила, действую­щая на каждую частицу жидкости, равна нулю потому, что сила тяжести уравновешивается инерционной силой переносного дви­жения.

Жидкость, находящаяся в условиях невесомости, теряет спо­собность образовывать свободную поверхность раздела с газооб­разной средой обычной формы. В резервуаре (баке), содержащем жидкость и газ, при этом происходит смешение жидкости и газа и образование двухфазной среды (суспензии жидкости и газа). Возможен и такой случай, когда газ сосредоточивается в центре бака в виде сферического ядра, а жидкость (смачивающая) обво­лакивает всю внутреннюю поверхность бака. Поэтому в гидрав­лических системах, которые должны работать в условиях неве­сомости, необходимо исключить возможность контакта жидкости с газом. Между жидкостью и газом должен быть разделитель виде подвижного поршня с пру­жинным и газовым подпором или в виде упругой диафрагмы (мем­браны) .

При отсутствии контакта жидкости с газом течение ее по тру­бопроводам под действием перепада давления, создаваемого насосом, газом или пружиной, в условиях невесомости будет отли­чаться от течения в обычных условиях лишь отсутствием влияния разности нивелирных высот. А в случае больших перепадов давления и при течении в замкнутых трубопроводах ни­какого различия между течениями в условиях невесомости и в. обычных условиях не будет.

Истечение жидкости через отверстия и насадки под достаточно большим напором в газовую среду при невесомости также не имеет существенных особенностей до тех пор, пока струя жидкости не потеряет своей кинетической энергии. Истечение через форсунку и распыливание жидкости происходит так же, как и обычно.

Существенно иным в условиях невесомости будет поведение жидкости, лишенной напора и соприкасающейся с воздухом (га­зом). В этом случае решающую роль приобретают силы поверх­ностного натяжения.

Если в «земных» условиях эти силы, как известно, вы­зывают подъем или опускание жидкости в капиллярах на высоту, обратно пропорциональную диаметру трубки и зависящую от рода жидкости, то в условиях невесомости силы поверхностного натя­жения вызывают непрерывное движение в трубке, опущенной одним концом в жидкость. Как показывают теоретические исследования, скорость течения жидкости при этом сначала нарастает до тех пор, пока сила трения не сделается равной силе поверхностного натя­жения. Затем скорость течения начнет постепенно уменьшаться вследствие того, что поверхность трения в трубке непрерывно уве­личивается.

Таким образом простая трубка в условиях невесомости может выполнять функцию небольшого насоса, причем совершенно без­различно, как направлена трубка, подающая жидкость.