Так же, как и для параллельных трубопроводов, имеем

В самолетных системах неизменность направления потоков часто обеспечи­вается установкой обратных клапанов.

Записав уравнение Бернулли для сечения М—М и для конеч­ного сечения, например, первого трубопровода, получим (пренебрегая разностью скоростных высот)

Будем иметь:

Аналогично для двух других труб можно записать:

Таким образом, получаем систему четырех уравнений с четырь­мя неизвестными. Решение удобно выполнить гра­фически. Для этого строим для каждого из трубопроводов зависи­мости p_M/ от Q_m по приведенным выше уравнениям, а затем выполняем их сложение так же, как складываются характеристики параллельно соединенных труб, т. е. складываем абсциссы (Q) при одинаковых ординатах (H_M). Полученная кривая представляет собой кривую потребного напора для разветвленного трубопровода, которая позволяет определять значения расходов по давлению или наоборот.

При обратном направлении потоков в трубах, т. е. от резервуаров 1, 2 и 3 к сечению М—М, в предыдущих уравнениях потери напора меняют знаки на обратные.

Возможен и такой случай, когда обратные клапаны в трубопро­водах отсутствуют и течение в них может быть как в одном, так и в другом направлениях. В этом случае построение суммарной кривой, т. е. сложение абсцисс при одинаковых ординатах, должно производиться с учетом знаков расходов.

Рассмотренный выше разветвленный трубопровод, а также тру­бопровод, составленный из нескольких параллельных труб, пред­ставляют собой разновидности сложного трубопровода. В общем случае, как ясно из определения, сложный трубопровод может состоять из последовательно и параллельно соединенных участков или разветвлений.

Расчет сложных трубопроводов как самотечных, так и питаемых насосом обычно производят графоаналитическим способом, т. е. с применением кривых потребного напора.

Расчет и построение этих кривых для сложного трубопровода в общем случае выполняются следующим образом. Сложный тру­бопровод разбивается на ряд простых. Рассчитывается каждый из этих простых трубопроводов и строятся кривые H_потр=f(Q) так, как было описано выше. Затем производится сложение этих кривых для параллельно соединенных участков или элементов разветвлен­ного трубопровода. Таким обра­зом, получается кривая потребного напора для параллельного со­единения (одного или нескольких) или разветвленного трубопро­вода. Далее выполняется сложение полученной кривой с кривыми для последовательно соединенных участков.

Руководствуясь этим правилом, можно построить кривую по­требного напора для любого сложного трубопровода как при тур­булентном, так и при ламинарном режиме течения.

Трубопровод с насосной подачей жидкости

Выше мы рассматривали по сути дела лишь отдельные участки простых и сложных трубопроводов, а не всю систему подачи жид­кости (кроме простейшей самотечной системы). В авиационной технике, как уже отмечалось, основным способом подачи жидкости является принудительная подача с помощью насоса.

Рассмотрим совместную работу трубопровода и насоса и принцип расчета тру­бопровода с насосной по­дачей жидкости.

Трубопровод с насос­ной подачей может быть разомкнутым, т.е. таким, по которому жидкость пе­рекачивается из одного места в другое, или замкнутым (кольцевым), в ко­тором циркулирует одно и то же количество жидко­сти.

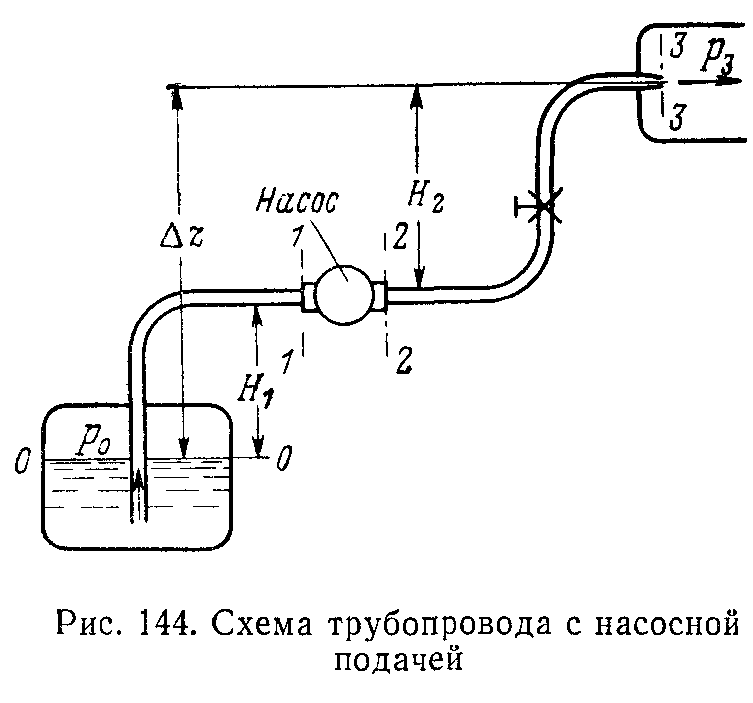
Рассмотрим вначале разомкнутым трубопровод (рис 144), по которому насос перекачивает жид­кость, например, из нижнего резервуара с давлением р_о в какую-либо камеру с давлением р_з или в Другой резервуар.

Высота расположения оси насоса относительно нижнего уровня (H₁) называется геометрической высотой всасывания, а трубопровод, по которому жидкость движется к насосу, — всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода, или верхнего уровня жидкости (H₂), называется геометрической высотой нагнетания, а трубопро­вод, по которому жидкость движется от насоса, — напорным трубопроводом или линией нагнетания.

Составим уравнение Бернулли для потока жидкости во всасы­вающем трубопроводе:

Записанное уравнение показывает, что процесс всасывания, т.е. подъем жидкости на высоту, сообщение ей кинетической энергии и преодоление всех гидравлических сопротивлений происходит зa счет использования (с помощью насоса) давления р_о. Так как это давление обычно бывает весьма ограниченным, то расходовать его нужно так, чтобы перед входом в насос остался еще некоторый запас давления p₁, необходимый для нормальной безкавитационной работы насоса. Поэтому расчет всасывающих трубопроводов должен быть особенно тщательным и точным.

Запишем уравнение Бернулли для движения жидкости по на­порному трубопроводу, т. е. для сечений 2—2 и 3—3:

Если напорный трубопровод заканчивается резервуаром, то скоростного напора в правой части уравнения не будет, но нужно учесть потерю напора на расширение.

Левая часть уравнения представляет собой удельную энергию жидкости на выходе из насоса.

Удельная энергия жидкости перед входом в насос:

Найдем приращение удельной энергии жидкости в насосе, т.е. определим ту энергию, которую приобретает, проходя через насос, каждая единица веса жидкости. Эта энергия сообщается жидкости насосом, поэтому она носит название напора, создаваемого насо­сом:

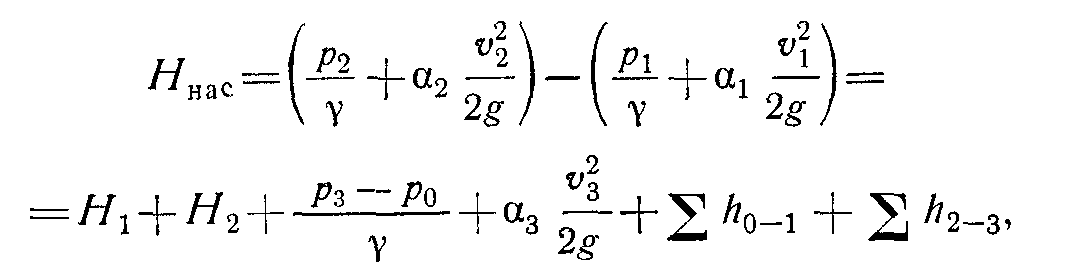
или

Можно рассматри­вать как бы увеличенную разность уровней, равную

Очевидно, что

Это равенство можно распространить на все случаи устойчи­вой работы насоса, соединенного с трубопроводом, и сформулиро­вать в виде следующего правила: при установившемся течении в трубопроводе насос развивает напор, равный потребному. Только при этом условии возможен устойчивый режим работы насоса. Это условие обычно реализуется автоматически.

На равенстве основывается метод расчета трубопро­водов, питаемых насосом, который заключается в совместном по­строении в одном и том же масштабе и на одном графике двух кривых: кривой потребного напора и характеристики насоса и в нахождении их точки пересечения.

Эта точка называется рабочей точкой, так как всегда реализуется режим работы насоса, соответствующий именно этой точке.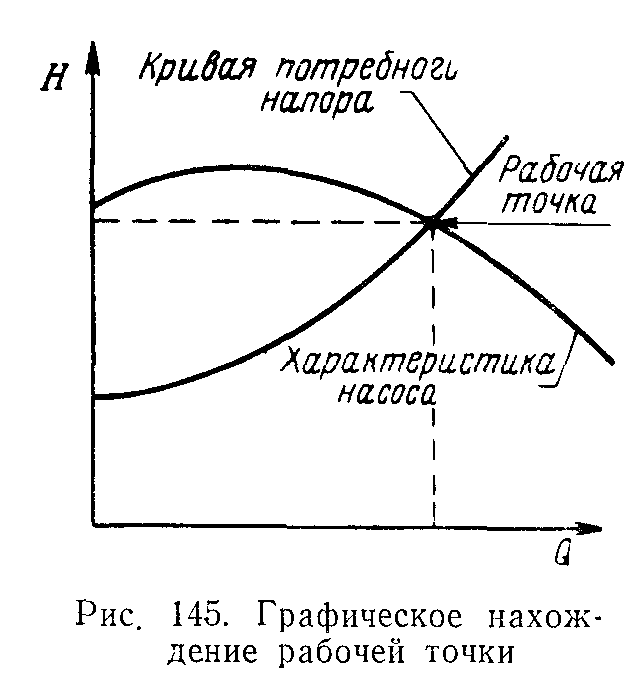

Чтобы получить другую рабочую точку, нужно или изменить степень открывания регулировочного крана (вентиля, задвижки), т. е., изменить характеристику трубопровода, или изменить число оборотов насоса, о чем подробнее будет сказано ниже.

Следует, однако, иметь в виду, что указанный расчетный прием для нахождения рабочей точки применим лишь в том случае, когда число оборотов привода насоса не зависит от мощности, потреб­ляемой насосом, т. е. от нагрузки на валу насоса. Это имеет место, например, при соединении насоса с электродвигателем переменного тока или с авиационным двигателем, мощность которого во много раз больше мощности насоса.

Если насос приводится в действие от какого-либо индивидуаль­ного двигателя внутреннего сгорания или от специальной турбины, мощность которых зависит от нагрузки на валу насоса, то расчет должен выполняться иначе. В этом случае следует строить кривые потребных и располагаемых мощностей по числам оборотов и по точке их пересечения определять рабочее число оборотов и мощ­ность.