Последовательное и параллельное соединение труб

Возьмем несколько труб, например 1, 2 и 3, различной длины, разного диаметра и содержащих различные местные сопротивле­ния, и соединим их последовательно (рис. 138). В результате по­лучим простой трубопровод переменного сечения.

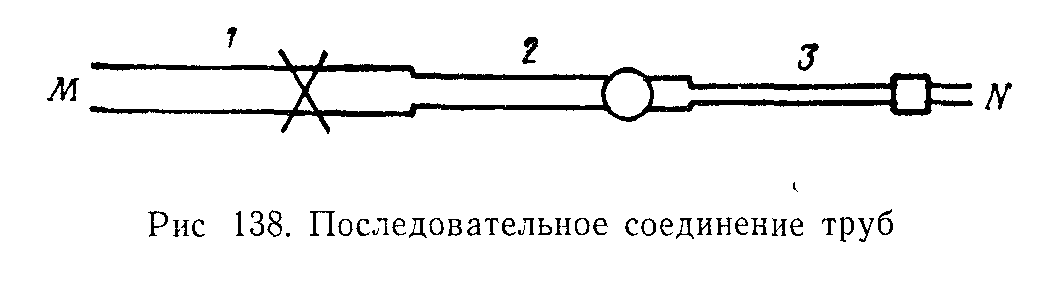
Совершенно очевидно, что при подаче жидкости по такому трубопроводу расход во всех последовательно соединенных трубах будет один и тот же, а полная потеря напора между точками М и N равна сумме потерь напора во всех последовательно соединен­ных трубах, т. е. имеем следующие основные уравнения:

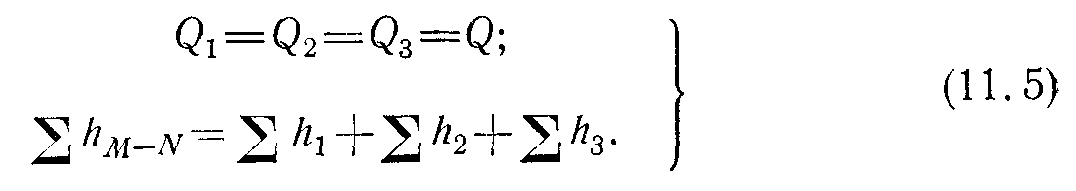
Эти уравнения определяют правило построения характеристик последовательного соединения труб.

Пусть нам даны (или мы построили сами) характеристики (1, 2, 3) трех трубопроводов (рис. 139). Для того чтобы построить ха­рактеристику М—N всего последовательного соединения, мы долж­ны в соответствии с системой уравнений (11.5) выполнить сло­жение потерь напора при одинаковых расходах, т. е. сложить орди­наты всех трех кривых при равных абсциссах.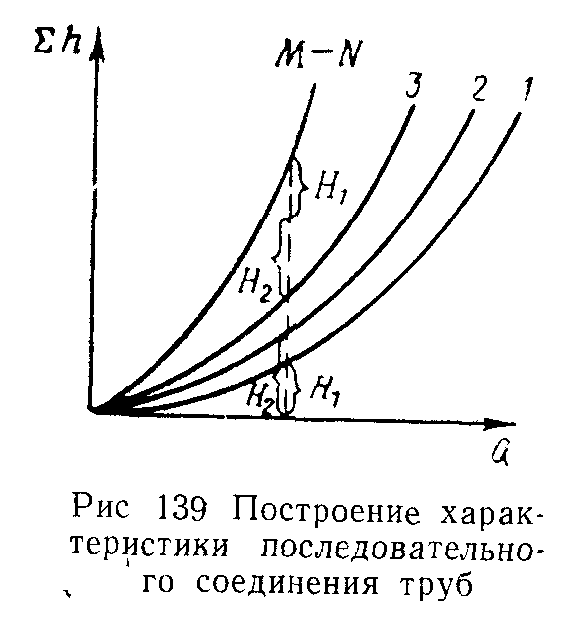

Так как в рассматриваемом более общем случае скорости в на­чале (М) и конце (N) трубопровода различны, то выражение по­требного напора для всего трубопровода М—N должно содержать разность скоростных напоров в конце и начале трубопровода, т. е.

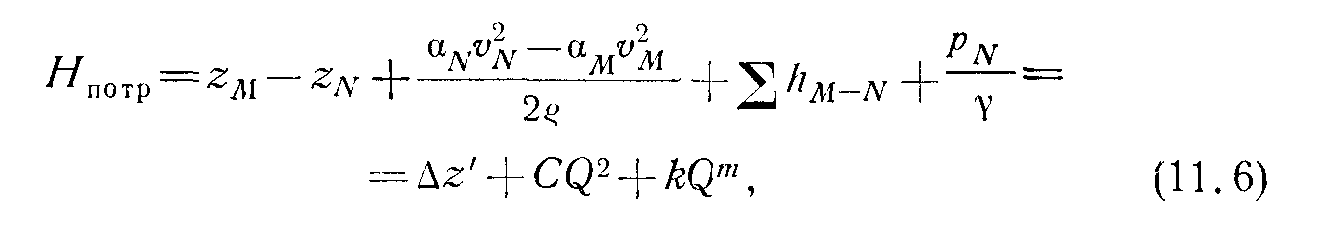
Где

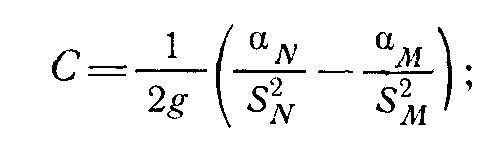
Рассмотрим теперь параллельное соединение несколь­ких различных трубопроводов (/, 2, 3) между точками М и N (рис. 140).

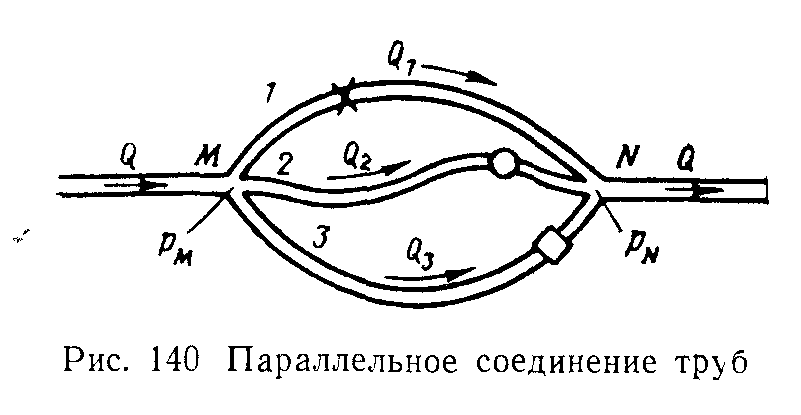
Обозначим: полные напоры в точках М и N соответственно Н_M и Н_N ; расход в основной магистрали (т. е. до разветвления и после слияния) Q, а в параллельных трубопроводах Q₁, Q₂ и Q₃; суммар­ные потери напора в этих трубопроводах h₁, h₂ и h₃.

Прежде всего запишем следующее очевидное уравнение:

Затем выразим потери напора в каждом из трубопроводов че­рез полные напоры в точках М и N, т. е.

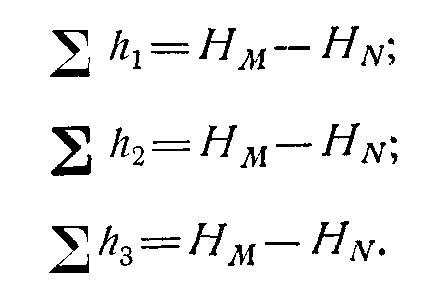
Отсюда делаем следующий важный вывод:

т. е. потери напора в параллельных трубопроводах равны между собой.

Эти потери можно выразить через соответствующие расходы в общем виде следующим образом:

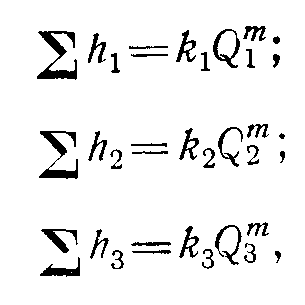
где коэффициенты k и показатель m определяются в зависимости от режима течения.

Получаем еще два уравнения:

Система уравнений позволяет решать, например, следующую типичную задачу: даны расход в основной магистрали Q и все размеры трубопроводов; определить расходы в параллельных трубопроводах.

Важное правило: для построения характеристики параллельного соедине­ния нескольких трубопроводов нужно сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах (h).

Изложенные соотношения и пра­вила для параллельных трубопрово­дов справедливы, разумеется, также в том случае, когда трубопрово­ды не сходятся в одной точке N, а подают жидкость в разные места, но с оди­наковыми давлениями и равными нивелирными высотами конечных сечений. Если же последнее условие не соблюдается, то рассматриваемые трубопроводы нельзя считать парал­лельными, а следует относить к раз­ряду разветвленных трубопроводов.

РАЗВЕТВЛЕННЫЕ ТРУБОПРОВОДЫ. РАСЧЕТ СЛОЖНОГО ТРУБОПРОВОДА В ОБЩЕМ СЛУЧАЕ

Условимся называть разветвленным трубопроводом совокуп­ность нескольких труб, имеющих одно общее сечение — место раз­ветвления или смыкания этих труб. Такие трубопроводы обычно имеются в самолетных топливных системах (основных и заправоч­ных) и в системах гидропередач, а также в стационарных системах подачи топлива на аэродромах.

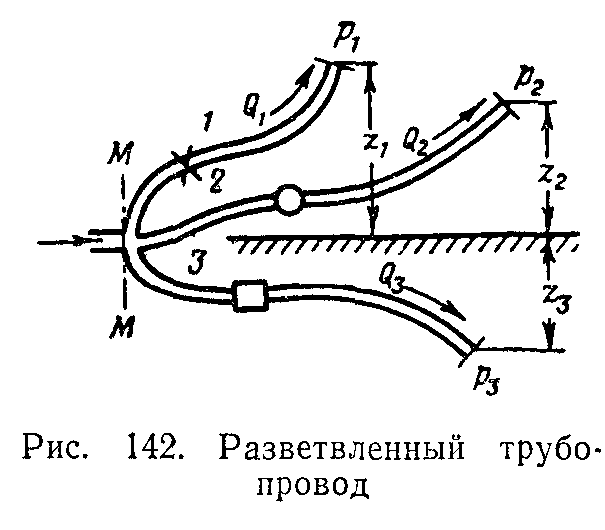
Пусть основной трубопровод имеет разветвление в сечении М—М, от которого отходят, например, три трубы (1, 2, 3) разных размеров и содержащих различные местные со­противления (рис. 142). Нивелирные высоты конечных сечений и давления в них пусть будут также различными. Найдем связь между давлением в сечении М—М (р_м) и расходами в трубах, считая направление течения в трубах за­данным (см. стрелки).