ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ

Простой трубопровод постоянного сечения

Все трубопроводы могут быть разделены на простые и сложные. Простым трубопроводом условимся называть трубопровод без раз­ветвлений, а сложным — трубопровод с одним или несколькими разветвлениями.

Жидкость движется по трубопроводу благодаря тому, что ее потенциальная энергия в начале трубопровода больше, чем в кон­це. Этот перепад (разность) уровней потенциальной энергии может быть создан тем или иным способом: работой насоса, давлением газа или за счет разности уровней жидкости.

В авиационной технике приходится иметь дело главным обра­зом с такими трубопроводами, движение жидкости в которых обус­ловлено работой насоса. В некоторых жидкостноракетных и других устройствах применяется так называемая газобаллонная подача жидкости, т. е. используется давление газа. Течение жидкости за счет разности уровней (разности нивелирных высот) осуществля­ется лишь в наземных условиях.

Пусть простой трубопровод постоянного сечения, расположен­ный произвольно в пространстве (рис. 134), имеет общую длину l и диаметр d и содержит ряд местных сопротивлений.

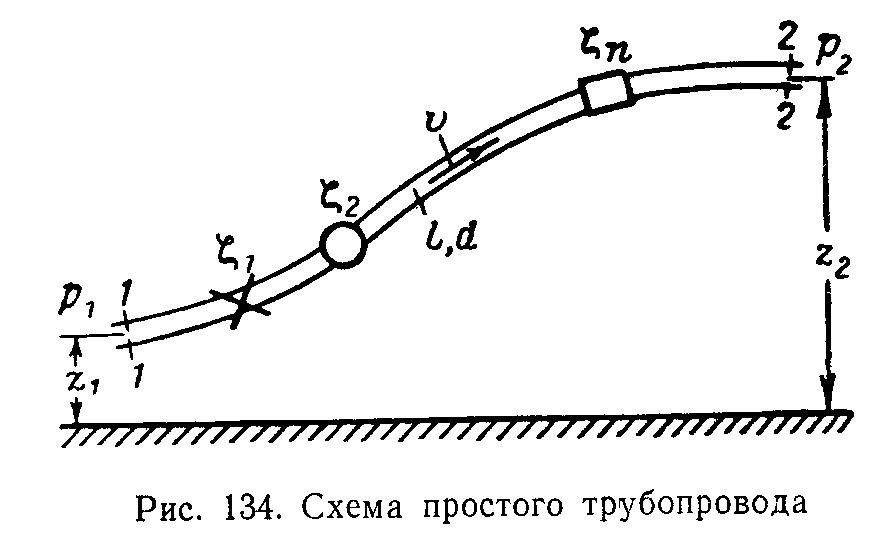
Ско­рость потока в сечениях вследствие постоянства диаметра тру­бы одинакова. Запишем уравнение Бернулли для сече­ний 1—1 и 2—2:

или

Пьезометрическую высоту в левой части уравнения назовем потребным напором H_потр. Если же эта величина задана, то будем называть ее располагаемым напором H_расп. Как видно из уравне­ния, этот напор складывается из геометрической высоты, на которую поднимается жидкость в процессе движения по трубопро­воду, пьезометрической высоты в конце трубопровода и суммы всех гидравлических потерь в трубопроводе.

Сумма двух первых слагаемых - статический на­пор и его можно представить как некоторую эквивалентную гео­метрическую высоту подъема жидкости z', а последнее слагаемое — как степенную функцию расхода, тогда

где величина k и показатель степени m имеют разные значения в за­висимости от режима течения.

Для ламинарного режима:

Для турбулентного режима:

Кривой потребного напора называется график зависимости по­требного напора от расхода жидкости в трубопроводе. Чем больше расход, который нужно подавать по трубопроводу, тем больше по­требный напор. При ламинарном режиме кривая потребного на­пора изображается прямой линией (или близкой к прямой), при турбулентном—параболой с показателем степени, равным двум или около двух. Величина z' поло­жительна в том случае, когда жидкость при движении по трубо­проводу поднимается с меньшей высоты на большую или движется в полость с повышенным давлением и отрицательна — при течении сверху вниз или в полость с разрежением.

Различные виды кривых потребного напора показаны на рис. 135 для ламинарного (а) и турбулентного (б) режимов. Кру­тизна кривой зависит от коэффициента k и возрастает с увеличени­ем длины трубопровода, с уменьшением диаметра, а также с уве­личением коэффициентов местных гидравлических сопротивлений в трубопроводе. Кроме того, при ламинарном режиме угол наклона прямой изменяется пропорционально вязкости жидкости).

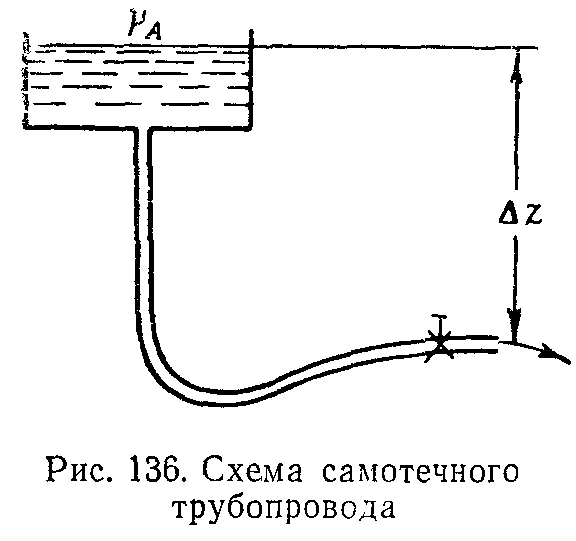
Точка пересечения кривой потребного напора с осью абсцисс при z0 (точка А) определяет собой расход при движении жид­кости самотеком, т. е. за счет лишь разности нивелирных высот z. Потребный напор в этом случае равен нулю, так как давление в начале и в конце трубопровода равно атмосферному (за нача­ло трубопровода считаем свободную поверхность в верхнем резер­вуаре); такой трубопровод условимся называть самотечным (рис. 136).

Если в конце самотечного трубопровода происходит ис­течение жидкости в атмосферу, то в уравнении для потребного на­пора к потерям напора нужно добавить скоростной напор.

Иногда вместо кривых потребного напора удобнее бывает поль­зоваться так называемыми характеристиками трубопровода.

Характеристикой трубопровода называется график зави­симости суммарной потери напора (или давления) в трубопроводе от расхода, т. е.

Таким образом, характеристика трубопровода представляет собой кривую потребного напора, сдвинутую в начало координат.

Рассмотрим возможные задачи на расчет простого трубопро­вода.

Задача 1. Дано: расход Q, давление р₂, свойства жидкости ( и ), все размеры трубопровода, а также материал и качество изготовления трубы (шероховатость). Найти потребный напор H_потр.

Решение выполняется в следующем порядке. По расходу и диа­метру трубопровода d находим скорость течения; далее опре­деляем число Re и режим течения. Затем по соответствующим фор­мулам или опытным данным оцениваем местные сопротивления.

Задача 2. Дано: располагаемый напор, свойства жидко­сти, все размеры трубопровода, а также шероховатость. Найти рас­ход Q.

Решение будет существенно различным для ламинарного и тур­булентного режимов. Поэтому задаемся режимом течения, основы­ваясь на вязкости жидкости .

1.При ламинарном режиме и при замене местных сопротивле­ний эквивалентными длинами задача решается просто: находится расход Q; при этом вместо H_потр подставляется H_расп.

2. При турбулентном режиме задача должна решаться методом последовательных приближений или графически.

В первом случае мы имеем одно уравнение (11. 1) с двумя не­известными Q и _т. Для решения задачи задаемся значением коэф­фициента _т с учетом шероховатости.

Решая уравнение относительно Q мы находим расход в первом приближении. По найденному Q определяем Re в первом приближении, а по Re — уже более точное значение _т. Снова подставляем полученное зна­чение _т в то же основное уравнение и решаем его относительно Q. Полу­чив расход во втором приближении, обнаружим большее или меньшее рас­хождение с первым приближением. Если расхождение велико, то расчет продолжаем в том же порядке. Раз­ница между каждым последующим значением Q и предыдущим будет делаться все меньше и меньше.

Расчет следует продолжать до тех пор, пока расхождение между последовательными значениями Q не окажется в пределах допу­стимой погрешности.

Обычно бывает вполне достаточно двух или трех приближений для получения приемлемой точности.

Для решения той же задачи графическим способом строят кри­вую потребного напора для данного трубопровода с учетом пере­менности _т, т. е. для ряда значений Q подсчитывают Re, _т и, на­конец, H_потр по формуле. Затем, построив кривою H_потр по Q и зная ординату H_потр = H_расп находят соответствующую ей абс­циссу, т. е. Q.

Задача 3. Дано: расход Q, располагаемый напор H_расп, свой­ства жидкости и все размеры трубопровода, кроме диаметра. Най­ти диаметр трубопровода.

Решение начинаем с того, что, основываясь на свойствах жидко­сти, задаемся режимом течения.

В случае ламинарного режима задача решается просто на осно­ве уравнения:

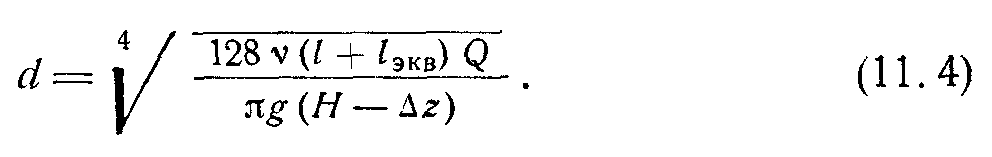
Определив d, выбираем ближайший больший стандартный диа­метр и по тому же уравнению уточняем значение напора при за­данном Q или наоборот.

При турбулентном режиме решение уравнения относительно d лучше всего выполнить следующим образом: задаемся рядом стандартных значений d и для заданного Q под­считываем ряд значений H_потр, затем строим график зависимости H_потр от d и по заданному H_расп по кривой определяем d, округляем его значение по стандарту и уточняем H_потр.

СИФОН

Сифоном называется такой простой самотечный трубопровод, часть которого расположена выше питающего его резервуара (рис. 137). Жидкость движется по сифону за счет разности уровней, причем сначала жидкость поднимается на высоту H₁ от свободной поверхности с атмосферным давлением, а затем спу­скается на высоту H₂.

Особенностью такого трубопровода является то, что давление жидкости по всей его восходящей линии и по части нисходящей меньше атмосферного.

Для того чтобы сифон начал подавать жидкость, необходимо весь его объем за­полнить жидкостью. Если в качестве си­фона используется шланг небольших размеров, то это заполнение легко осу­ществить предварительным погружением его в жидкость или отсосом воздуха из нижнего конца.

Если же сифон выполняется в виде стационарного металлического трубопро­вода, то необходимо в его верхней точке предусмотреть кран для отсоса воздуха. Воздух можно отсосать любым объемным насосом или эжектором. Запишем уравнение Бернулли для сечений 0—0 и 2—2, где считаем скорости равными нулю, а давление—атмо­сферным:

или

Таким образом, расход через сифон определяется разностью уровней Н и сопротивлением трубопровода, но не зависит от вы­соты подъема. Однако это верно лишь до известных пределов. С увеличением высоты H₁ уменьшается абсолютное давление в верхнем сечении сифона 1—1 (p₁). Когда это давление делается равным упругости насыщенных паров, то начинается кавитация и расход уменьшается, а затем образуются скопления паров (па­ровые пробки) и подача жидкости прекращается.

Поэтому при устройстве сифона необходимо следить за тем, чтобы давление в его верхней точке не было слишком малым. Если известен расход жидкости через сифон и все размеры, то аб­солютное давление может быть найдено из уравнения Бернулли для сечений 0—0 и 1—1, имеющего вид

Если же известно минимально допустимое давление p₁, то, зная расход, можно из того же уравнения найти максимально допусти­мую высоту H₁.