МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ

ОБЩИЕ СВЕДЕНИЯ О МЕСТНЫХ СОПРОТИВЛЕНИЯХ. ВНЕЗАПНОЕ РАСШИРЕНИЕ РУСЛА

Гидравлические потери энергии делятся на две категории: местные потери и потери на трение. Рассмотрим потери, обусловленные так называемыми местными гидравлическими сопротивлениями, т. е. такими элементами трубопроводов, в который вследствие измене­ния размеров или конфигурации русла происходит изменение ско­рости потока и обычно возникают вихреобразования.

Общий способ их выражения, основанный на экспери­ментальных данных:

Задача теперь заключается в том, чтобы научиться определять коэффициенты для различных местных сопротивлений.

Простейшие местные гидравлические сопротивления можно раз­бить на следующие группы и подгруппы:

1) расширение русла - внезапное, плавное;

2) сужение русла - внезапное, плавное;

3) поворот русла - внезапный, плавный.

Более сложные случаи местных сопротивлений представляют собой соединения или комбинации перечисленных простейших со­противлений.

Рассмотрим простейшие местные сопротивления в том порядке, как они перечислены выше, при турбулентном режиме течения. Следует отметить, что коэффициенты сопротивления при турбулентном течении определяются почти исключительно формой местных сопротивле­ний и очень мало меняются с изменением размеров русла, скорости потока и вязкости жидкости, т. е. с изменением числа Re. Поэтому их обычно считают от числа Re независящими, что означает квад­ратичный закон сопротивления, или автомодельность. Местных со­противлений при ламинарном режиме мы коснемся в конце главы.

Значения коэффициентов местных сопротивлений в большин­стве случаев получают из опытов и затем пользуются эксперимен­тальными формулами или графиками.

Однако для случая внезапного расширения русла при турбу­лентном течении потерю напора можно достаточно точно найти чисто теоретиче­ским путем.

В незапное расширение русла (трубы) и соответствующая ему схема течения по­казаны на рис. 69.

Поток срывается с угла и расширяет­ся не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы получаются ви­хреобразования, которые и являются при­чиной потерь энергии в данном случае.

При этом, как показывают наблюде­ния, происходит непрерывный обмен час­тицами жидкости между основным пото­ком и завихренной его частью.

Возьмем два сечения потока. Так как по­ток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту большую, чем первый; но, если бы потерь напора в данном месте не было, то второй пьезометр показал бы еще большую высоту. Та высота h, которую мы здесь как бы недополучаем, и есть местная потеря напора на расширение.

В результате расчетов можно получить следующее выражение:

т. е. что потеря напора (удельной энергии) при внезапном рас­ширении русла равна скоростному напору, подсчитанному по разности скоростей. Это положение часто называют теоремой Борда - Карно.

Полученный результат можно записать еще в следующем виде:

Следовательно, для случая внезапного расширения русла коэф­фициент сопротивления равен

Доказанная теорема, как и следовало ожидать при сделанных допущениях, хорошо подтверждается опытом при турбулентном режиме течения и широко используется в расчетах.

В том частном случае, когда площадь S₂ весьма велика по срав­нению с площадью S₁ и, следовательно, скорость ₂ можно считать равной нулю, потеря на расширение равна:

т. е. теряется весь скоростной напор, вся кинетическая энергия, которой обладает жидкость; коэффициент сопротивления в этом случае равен 1. Такому случаю соответствует, например, подвод жид­кости по трубе к резервуару достаточно больших размеров.

Следует подчеркнуть, что рассмотренная потеря напора (энер­гии) при внезапном расширении русла расходуется, можно счи­тать, исключительно на вихреобразования, связанные с отрывом потока от стенок, т. е. на поддержание непрерывного вращатель­ного движения жидких масс и постоянное их обновление (обмен). Поэтому этот вид потерь энергии, пропорциональных квадрату ско­рости (расхода), называют потерями на вихреобразования.

Кроме того, эти потери энергии часто называют еще потерями на удар, так как здесь имеется довольно резкое уменьшение ско­рости, как бы удар быстродвижущейся жидкости о жидкость, дви­жущуюся медленно или вовсе неподвижную.

Диффузоры

Постепенно расширяющаяся труба называется диффузором. Течение жидкости в диффузоре сопровождается уменьшением ско­рости и увеличением давления. Частицы движущейся жидкости преодолевают нарастающее давление за счет своей кинетической энергии, но последняя уменьшается вдоль диффузора, а также в направлении от оси к стенке. Слои жидкости, прилежащие к стен­кам, обладают столь малой кинетической энергией, что подчас оказываются не в состоянии преодолевать повышенное давление. Они останавливаются, или, даже начинают двигаться обратно. Ос­новной поток наталкивается на эти противотоки, возникают вихре­образования и отрыв потока от стенки (рис. 70). Интенсивность этих явлений возрастает с увеличением угла расширения диффу­зора, а вместе с этим растут и потери на вихреобразования в диф­фузоре. Кроме того, в диффузоре имеются обычные потери на тре­ние, подобные тем, которые возникают в трубах постоянного се­чения.

Полную потерю напора в диффузоре мы будем условно рассматривать как сумму двух слагаемых:

Потерю напора на трение можно приближенно подсчитать сле­дующим способом. Рассмотрим круглый диффузор с прямолиней­ной образующей и с углом  при вершине.

Для него:

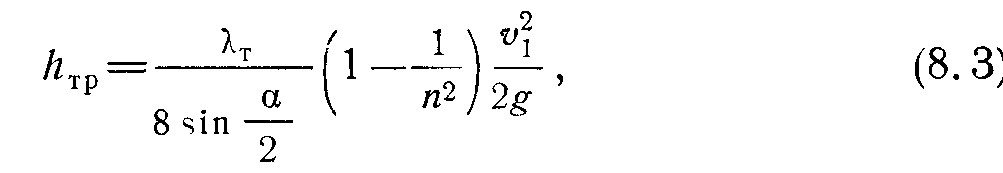
где ₁—скорость в начале диффузора;

-так называемая степень расширения диффузора.

Второе слагаемое—потеря напора на расширение (на вихре­образования) имеет в диффузоре ту же природу, что и при вне­запном расширении, но меньшую величину, поэтому оно обычно выражается по той же формуле, но с поправоч­ным коэффициентом k, меньшим единицы, т. е.

Так как в диффузоре мы имеем по сравнению с внезапным рас­ширением как бы смягченный удар, то и коэффициент k часто на­зывают коэффициентом смягчения удара. Численное значение этого коэффициента для диффузоров с углами конусности а по­рядка 5—20° можно определять по следующей экспериментальной формуле И. Е. Идельчика

или по приближенной формуле Флигнера

Исходное выражение можно переписать в следующем виде:

а коэффициент сопротивления диффузора можно окончательно выразить следующей формулой:

С уве­личением угла  при заданных _т и n первое слагаемое обусловленное трением, уменьшается, так как диффузор дела­ется короче, а второе слагаемое, обус­ловленное вихреобразованиями и отры­вом потока, возрастает.

При уменьшении же угла вихреобразования уменьшаются, но возра­стает трение, так как при заданной сте­пени расширения диффузор удлиня­ется и поверхность его трения увели­чивается.

Функция имеет минимум при некотором наивыгоднейшем опти­мальном значении угла а (рис. 72):

При подстановке в эту формулу значения коэффициента потерь па трение порядка 0,015— 0,025 и соотношения площадей в пре­делах n = 2—4 получим наивыгоднейший угол диффузора в среднем порядка 6°, что соответствует экспериментальным данным.

На практике в целях сокращения длины диффузора при задан­ном п обычно принимают несколько большие углы, а именно: 7—9°. Те же значения угла можно рекомендовать и для квад­ратных диффузоров.

Для прямоугольных диффузоров с расширением в одной пло­скости (плоские диффузоры) оптимальный угол больше, чем для круглых и квадратных, и составляет 10—12°.

Если по условиям габаритов невозможно применение углов, близких к наивыгоднейшим, то при >15—25° целесообразно от­казаться от диффузора с прямолинейной образующей и применить один из специальных диффузоров, например, диффузор, обеспечи­вающий постоянный градиент давления вдоль оси:

Примерные очертания такого диффузора даны на рис. 73.

Уменьшение потери энергии в таких диффузорах по сравнению с прямолинейными тем больше, чем больше угол , и доходит до 40% при углах порядка 40—60°. Кроме того, поток в криволи­нейном диффузоре отличается большей устойчивостью.

Хорошие результаты дает также ступенчатый диффузор, со­стоящий из обычного диффузора с оптимальным углом и следую­щего за ним внезапного расширения (рис. 74). Последнее не вы­зывает больших потерь энергии, так как скорости в этом месте сравнительно малы. Общее сопротивление такого диффузора зна­чительно меньше, чем обычного диффузора такой же длины и с той же степенью расширения.