44. Интегрирование дифференциального бинома.
Интегрирование дифференциального бинома
Дифференциальными биномами, или биномиальными дифференциалами называются дифференциалы вида
|
xm (a + bxn )p dx, |
|
где a и b — вещественные коэффициенты, отличные от нуля, m , n , p — рациональные числа, p ≠ 0 .
Условия Чебышева
Интеграл от дифференциального бинома выражается через конечную комбинацию элементарных функций только в следующих трех случаях:
1) p — целое число.
Подстановка x = ts , где s — общий знаменатель дробей m и n , приводит к интегралу от рациональной функции.
2)
m + 1 |
n |
— целое число.
Подстановка
|
x = n√
, ts = a + bxn , |
|
где s — знаменатель дроби p , приводит к интегралу от рациональной функции.
3)
m+ 1 |
n |
+ p — целое число.
Подстановка
|
x = n√ bts − b , ts = b + ax−n , |
|
где s — знаменатель дроби p , приводит к интегралу от рациональной функции.
45. Геометрический и физический смысл определенного интеграла.
Физический смысл: 1) если задана скорость как функция от времени, то путь за время Т равен интегралу от скорости по времени; 2) если задано ускорение как функция от времени, то изменение скорости равно интегралу от ускорения по времени; Геометрический смысл: если функция y(x) больше нуля на промежутке [a;b], то площадь криволинейной трапеции, ограниченной графиком функции, осью ОХ и двумя прямыми х=а и х=b, равна интегралу от этой функции по переменной х на данном промежутке.
46. Достаточное условие существования определенного интеграла.
Условия интегрирования f(x) принадлежит [a,b]
непр на f(x) принадлежит [a,b]
ограничена f(x) на отрезке [a,b] и нерп f(x) на отрезке [a,b] , кроме конечного числа точек разрыва 1 рода.
47. Линейность и аддитивность определенного интеграла.
48. Формула Ньютона-Лейбница.
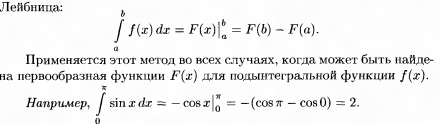
49. Интегрирование методом подстановки.
50. Интегрирование по частям.
51. Интегрирование четных и нечетных функций на симметричных отрезках.
52.
Основные формулы приближенного
вычисления определенного интеграла.
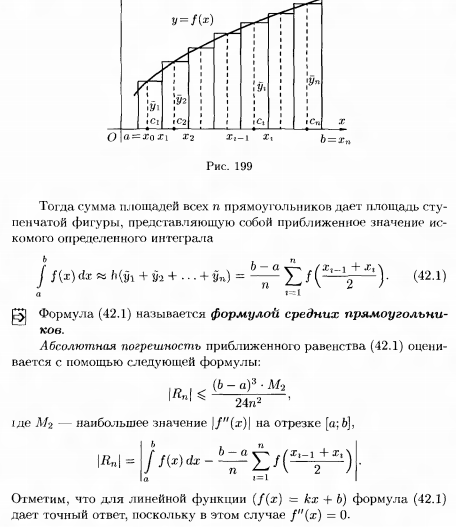
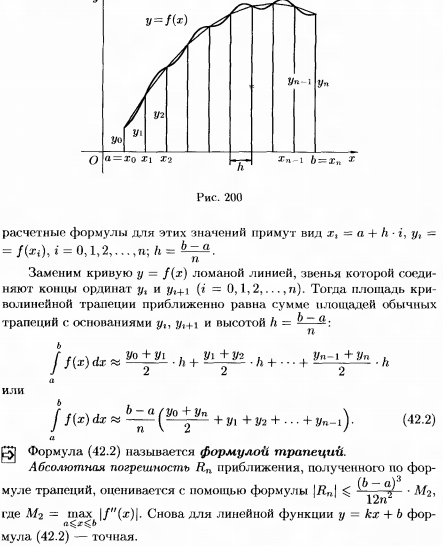
53. Определение несобственного интеграла I рода.
54. Признаки сходимости несобственного интеграла I рода.
55. Несобственные интегралы II рода. Признаки сходимости несобственного интеграла II рода.
1)1.конечный промежуток интегрирования
2.фун. имеет бескон.разрыв.
2)
56. Вычисление сходящихся несобственных интегралов.
57. Вычисление площадей плоских фигур. Вычисление длины дуги плоской кривой.
58. Вычисление объема тел и объема тел вращения
.
59. Основные методы интегрирования.