1. Понятие множества. Операции над множествами.

Мн-во – совокупность объектов, обладающих определенным св-вом. Пересечением двух мн-в А и В н-ся мн-во С, состоящее из Эл-ов, принадлежащих как мн-ву А, так и мн-ву В.(А={1,2,3}, B={2,5}, AΩB={2}) Объединением двух мн-в А и В н-ся мн-во С, состоящее из Эл-ов, принадлежащих хотя бы одному из мн-в А или В.(A={1,2,3}, B={2,5} AuB={1,2,3,5}Разностью С двух мн-в А и В н-ся мн-во, состоящ. Из Эл-ов мн-ва А и не принадл. В(Разностью мн-ва целых чисел и мн-ва четных чисел явл. Мн-во нечетных чисел) Если А подмн-во В, то разность В\А н-ся дополнением А до В. Дополнением мн-ва А н-ся мн-во, состоящ. Из Эл-ов универсального мн-ва не принадлежащих мн-ву А. 2. Рациональные числа. Иррациональные числа. Понятие действительного числа.

Рациональные числа – можно представить в виде конечной дес.дроби, либо бесконечной дес.дроби.(Q)Корень 2 не рационал

Иррациональные - это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби. Действительные числа – математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений ^[2].

3. Основные свойства действительных чисел. Метод математической индукции.

Упорядоченность – если A, B два разлин.действ число, то A<B или B<A.

Плотности – между 2 различн. A,B есть бесконечное множество R.

Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.

Метод математической индукции состоит в следующем:

Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:

1.P(1) является истинным предложением (утверждением);

2.P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).

Таким образом метод математической индукции предполагает два этапа

1.Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).

2.Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).

4. Определение функции.

5. Способы задания функции. График функции.

Задать фун. – это задать обл.опред,знач. И зак.соотв.

1)Аналитический – Заакон соотв.задаётся с помощью формулы

2)Графически3)Таблиный4)Компьютерный

График фун.

График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента  , а ординаты — соответствующими значениями функции  .

Обычно рассматриваются графики вещественных скалярных функций одного вещественного переменного  , которые являются множеством точек плоскости  .

6. Обратная функция. Сложная функция.

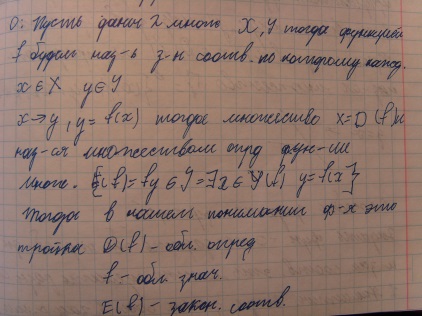
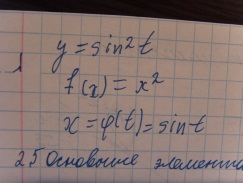
7. Основные элементарные функции.

Показательные

Степенные

Логарифмические

Триганометрические

Обратные

8. Определение предела функции на «языке последовательностей» и по Коши.

на «языке последовательностей», или по Гейне Постоянное число А называется предел функции f(x) при x→a, если для всякой последовательности {x_n} значений аргумента, стремящейся к а, соответствующие им последовательности {f(x_n)} имеют один и тот же предел А. на «языке ε», или по Коши Число А называется пределом функции в точке х_о (или при х→х_о), если для любого положительного ε найдется такое положительное число δ, что для все х¹х_о, удовлетворяющих неравенству |х-х_о|<δ, выполняется неравенство |ƒ(х)-А|<ε.