18. Установление факта наличия корреляционной связи между признаками.

Для этого используется ряд специфических методов. Рассмотрим основные из них:

1. параллельное сопоставление рядов значений результативного и факторного признака: значения факторного признака строят в порядке возрастания, т.е. строят ранжированный ряд признака и рядом располагают соответственные значения результативного признака. Если имеет тенденцию к нарастанию, то говорят о возможном наличии прямой корреляционной связи. Если имеет тенденцию к уменьшению, то говорят о возможном наличии обратной корреляционной связи. 2. метод корреляционных таблиц: применяется наиболее часто. Значения определяют столбцы корреляционной таблицы, а значения определяют строки корреляционной таблицы. На пересечении и стоит число, которое показывает, сколько раз встречается данная пара значений и . По расположению основной массы частот судят об отсутствии или о наличии той или иной корреляционной зависимости. Если основная масса частот корреляционной таблицы расположена по диагонали от нижнего левого угла к верхнему правому углу таблицы, то можно говорить о наличии обратной корреляционной зависимости, т.е. с увеличением значения имеют тенденцию уменьшаться.

3. метод групповых таблиц: разбивает на группы и для каждой группы определяют среднюю арифметическую групповую. Групповая таблица представляет собой таблицу из 2-х столбцов: 1 столбец – значения признака (дискретные или интервалы), 2 столбец – групповые средние . Далее в групповой таблице рассматривается тенденция изменения . Если с увеличением имеет тенденцию к увеличению, то говорят о возможном наличии прямой корреляционной зависимости. Если имеет тенденцию к уменьшению, то говорят о возможном наличии обратной корреляционной связи.

4. графический метод: предполагает построение в координатах поля корреляции и (или) эмпирической линии связи. Для построения эмпирической линии связи в осях координат отобразим точки с координатами: абсцисса – значение , ордината – значение . Эмпирическая линия вязи – это графическая иллюстрация групповой таблицы. Если имеется несколько признаков-факторов и один признак-результат, то необходимо попарно рассмотреть каждый признак-фактор в паре с признаком-результатом и установить факт наличия связи.

19. Измерение степени тесноты корреляционной связи (эмпирическое корреляционное отношение).

Этот показатель используется в том случае, если корреляционная зависимость, а именно график эмпирической линейной связи представляет собой кривую линию. Обозначается .

Пусть имеем пар значений 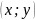, – признак-фактор, - признак-результат.

Если использовать признак-фактор в качестве группировочного признака, то все значения признака-результата разбиваем на совокупностей с соответствующими объемами.

Пусть для каждой группы рассчитали групповые средние

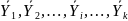
и определили групповые дисперсии

Тогда, согласно свойству средней арифметической, средняя арифметическая всей совокупности равна средней арифметической взвешенной групповых средних

Согласно свойству дисперсии, дисперсия всей совокупности равна сумме 2-х дисперсий: межгрупповой дисперсии и средней внутригрупповых дисперсий

показывает, насколько групповые средние отличаются от общей средней, т.е. показывает как влияет группировочный признак (признак-фактор) на признак-результат ,

представляет собой среднюю арифметическую взвешенную групповых дисперсий

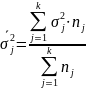
характеризует ту часть изменчивости признака , которая обусловлена всеми факторами, за исключением признака-фактора .

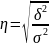
Эмпирическое корреляционной отношение показывает, какую часть, долю составляет изменчивость, обусловленная от всей изменчивости признака .

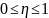η = 0 – связи нет

η = 1 – жесткая η → 1 – теснее связь