№1. Ряды распределения и их основные характеристики. Интервальный дискретный вариационные ряды.

Вариационный ряд – это последовательность значений наблюдаемого признака, которые записаны в порядке их поступления. Если значения признака разместить в порядке возрастания, то эта операция называется ранжированием, а ряд называется ранжированным.

Варианты – это различные значения признака.

Варьирование – это изменение в значении признака.

В зависимости от значений принимаемых признаков, признаки делятся на дискретно варьирующие и непрерывно варьирующие.

Дискретный вариационный ряд строится для дискретно варьирующего признака. В качестве примера рассмотрим тарифные разряды 100 рабочих. Построим дискретный ранжированный ряд этих рабочих:

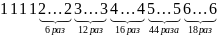
Частота варианта ( ) – это число, которое показывает, сколько раз встречается вариант в ряде наблюдений.

Если - количество значений наблюдаемого признака, то

Частость варианта (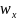 ) - это отношение частоты варианта к общему числу наблюдений:

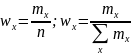
Накопленная частота ( ) – это число, которое показывает, сколько раз встречается вариант , значение которого меньше заданного значения .

Наколенная частость ( ) – это отношение накопленной частоты к общему числу наблюдений:

Дискретный вариационный ряд – это таблица, где указаны значения дискретного признака , а также частоты, частости, накопленные частоты и накопленные частости.

Изобразим дискретный вариационный ряд для нашего примера:

1	4	0	0,04	0
2	6	4	0,06	0,04
3	12	10	0,12	0,1
4	16	22	0,16	0,22
5	44	38	0,44	0,38
6	18	82	0,18	0,82
> 6	0	100	0	1

Если дискретный вариационный ряд строится только для дискретно варьирующего признака, то непрерывный вариационный ряд строится как для непрерывного, так и для дискретного признака, ели количество вариантов очень велико.

В случае непрерывного вариационного ряда указываются не конкретные значения , а их интервалы, тогда , , , называются интервальными.

Интервальная частота – это число, которое показывает, сколько раз значение признака попадает в интервал.

Интервальная частость – это отношение интервальной частоты на общее количество наблюдений.

Накопленная интервальная частота – это число, которое показывает сколько раз встречающееся значение признака будет строго меньше, чем верхняя границы интервала. Это частоты, накопленная к концу интервала.

Интервальная накопленная частость – этот отношение накопленной интервальной частоты к общему количеству наблюдений. Пример:

0-10	10	0,10	10	0,1
10-20	15	0,15	25	0,25
20-30	50	0,50	75	0,75
30-40	20	0,20	95	0,95
40-50	5	0,05	100	1

Для первого интервала его накопленная интервальная частота равна его частоте. Для последнего интервала накопленная интервальная частота равна . Для последнего интервала накопленная интервальная частость равна 1.

От интервального вариационного ряда можно перейти к дискретному, если в качестве варианта принять середины интервалов.

№2. Построение интервального вариационного ряда. Графическое изображение вариационных рядов.

Интервальный вариационный ряд – это таблица, где указаны интервалы значений , а также интервальный частоты, интервальные частости, накопленные интервальные частоты и накопленные интервальные частости.

Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов и в соответствии с ней группировать результаты наблюдений.

Чаще всего используются интервалы одинаковой ширины.

Графическое изображение вариационных рядов:

1. Полигон служит для изображения дискретного вариационного ряда. По оси абсцисс откладывают значения , а по оси ординат – частоты, либо частости. Полученные точки соединяют ломаной линией.

2. Гистограмма – это графическое изображение используется для непрерывных вариационных рядов. По оси абсцисс используются интервалы, а по оси ординат интервальные частоты или интервальные частости в виде горизонтальных линий.

3. Кумулятивная кривая служит для изображения и дискретных, и интервальных вариационных рядов. В случае дискретного вариационного ряда по ос абсцисс откладываются дискретные значения , а по оси ординат накопленные частоты или накопленные частости. Полученные точки соединяют ломаной линией.

В случае интервального вариационного ряда откладывают интервалы. Верхним границам интервалов соответствуют , . Нижней границе первого интервала соответствует 0, а верхней границе последнего 1.

№3. Степенные средние величины. Основные свойства средней арифметической.

Средние величины являются обобщенными характеристиками совокупности по определенному признаку. В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами, и находят выражение общие закономерные черты, свойственные всей совокупности явления.

Запишем вариационный ряд наблюдаемого признака:

- степенная средняя -го порядка

Основные свойства средней арифметической:

1. Сумма отклонений результатов наблюдений от средней арифметической равна нулю.

2 Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то средняя арифметическая уменьшится (увеличится) на то же число.

3. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число раз, то средняя арифметическая уменьшится (увеличится) во столько же раз.

4. Если ряд наблюдений состоит из групп наблюдений, то средняя арифметическая всего ряда равна взвешенной средней арифметической групповых средних, причем весами являются объемы групп :

5. Средняя арифметическая для сумм (разностей) взаимно соответствующих значений признака двух рядов наблюдений с одинаковыми числами наблюдений равна сумме (разности) средних арифметических этих рядов:

Следствие. Средняя арифметическая алгебраической суммы соответствующих значений признака нескольких рядов наблюдений равна алгебраической сумме средних арифметических этих рядов.

№4. Позиционные средние. Логическая формула средней.

Медианой ( ) называют значение признака, приходящегося на середину ранжированного ряда наблюдений.

Если проведено нечетное число наблюдений , а результаты наблюдений проранжированы и выписаны в следующий ряд:

На середину ряда приходится значение , следовательно .

Если проведено четное число наблюдений , то на середину ранжированного ряда приходятся значения и 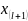. В этом случае за медиану принимают среднюю арифметическую значений и :

Для интервального вариационного ряда медиана определяется по формуле:

где - начало медианного интервала,

( ) – частота (частость), накопленная к началу медианного интервала;

( ) – частота (частость) медианного интервала,

- величина медианного интервала.

Медианным называется интервал, у которого первый раз накопленная частота (частость) станет равной или более половины всех наблюдений (≥0,5).

Модой ( ) называют такое значение признака, которое наблюдается наибольшее число раз.

Для дискретного вариационного ряда модой является вариант, которому соответствует наибольшая частота (частость).

В случае интервального вариационного ряда мода вычисляется по следующей формуле:

где - начало модального интервала, т.е. такого, которому соответствует наибольшая частота (частость),

( ) – частота (частость) модального интервала,

( ) – частота (частость) интервала, предшествующего модальному,

( ) – частота (частость) интервала, следующего за модальным.

Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или логическую формулу средней (ЛФС):

№5. Показатели абсолютной и относительной вариации ряда распределения. Свойства эмпирической дисперсии.

Средние величины характеризуют центр распределения статистических величин, т.е. значения, вокруг которых группируются значения наибольших признаков. Средние величины не характеризуют изменчивость статистических величин. Для характеристики изменчивости (вариации) используют показатели вариации статистических величин, которые могут быть 2-х видов: абсолютные и относительные.

Абсолютные показатели вариации:

1. размах вариации (используется редко):

2. среднее линейное отклонение – это средняя величина взятых по модулю отклонений наблюдаемого признака от средней арифметической величины:

3. среднее квадратическое отклонение (используется наиболее часто):

– дисперсия

Данные показатели применяются для оценки вариации в том случае, если в качестве средней величины используется средняя арифметическая.

4. дисперсия – средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий:

а)Простая дисперсия для несгруппированных данных

б)Взвешенная дисперсия для вариационного ряда

Квартильное отклонение используется при оценке изменчивости, если в качестве средней величины используется медиана.

Для сравнения изменчивости одноименных величин, имеющих разные величины средней, и для сравнения изменчивости разноименных величин используются относительные показатели вариации:

1. коэффициент осцилляции:

2. относительный коэффициент линейного отклонения:

3. коэффициент вариации:

Свойства эмпирической дисперсии:

1. Дисперсия постоянной величины равна нулю.

2. Если все результаты наблюдений уменьшить (увеличить) на одно и ту же число, то дисперсия не изменится.

3. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число раз , то дисперсия уменьшится (увеличится) в раз.

4. Дисперсию можно определить как разность между средней арифметической квадратов наблюдения и квадратом средней арифметической:

5. Если ряд наблюдений состоит из групп наблюдений, то дисперсия всего ряда равна сумме средней групповых дисперсий и межгрупповой дисперсии:

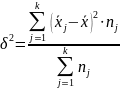
где - дисперсия -ой группы наблюдений,

- средняя арифметическая -ой группы наблюдений,

- средняя арифметическая всего ряда наблюдений,

- объем -ой группы наблюдений.

6. Относительные показатели вариации.

-коэффициент вариации

-коэффициент осцилляции

-относительное линейное отклонение

Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг общей средней.

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений (модуль отклонений) от средней величины.

3. Коэффициент вариации - отношение среднего квадратического отклонения к средней арифметической, применяется для сравнения вариаций различных признаков, используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.

№7. Программно-методологическая часть статистического наблюдения.

Информация, полученная в результате статистического наблюдения должна удовлетворять требованиям достоверности, полноты и своевременности.

Статистическое наблюдение должно быть организовано как планомерное, массовое и систематическое.

Объект наблюдения – общественное явление или процесс, которые подлежат исследованию.

Единица наблюдения – составной элемент объекта наблюдения, представляющий собой источник информации.

Единица совокупности – составной элемент как объекта наблюдения, так и единицы наблюдения, который служит их основой и обладает признаками, подлежащими регистрации в процессе наблюдения.

Единицы наблюдения называются отчетными единицами, если наблюдение проводится в форме собрания отчетности.

Учесть все признаки, которыми обладает единица совокупности не всегда представляется возможным. Поэтому при подготовке статистического наблюдения необходимо решить вопрос о том, какие признаки будут регистрироваться.

Программа должна отвечать следующим требованиям:

1. в программе должны быть даны ответы на те вопросы, которые действительно необходимы и ответы будут использованы либо при обработке информации, либо в контрольных целях;

2. программа должна быть по возможности построена так, чтобы ответы на один вопрос могли использоваться для контроля ответов на другие;

3. все вопросы программы должны быть четкими и предельно ясными, не допускающим разных толкований;

4. для проведения наблюдения необходим свой инструментарий, в частности формуляры и инструкции.

Формуляр – специальный документ, в котором фиксируются ответы на вопросы программы. Различают 2 разновидности формуляров:

1. формуляр-карточка: предназначается для отражения одной единицы статистической совокупности;

2. формуляр-список: фиксирует сведения о нескольких единицах совокупности.

Инструкция – письменные указания и разъяснения по выполнению программы наблюдения.

Вопрос №8. Виды и способы статистического наблюдения.

Виды статистического наблюдения классифицируются:

1. по степени охвата исследуемой совокупности:

- сплошное (полное): охватывает все единицы изучаемой совокупности.

- не сплошное (частичное): охватывает определенную часть изучаемой совокупности. Делится на выборочное наблюдение, монографическое наблюдение и наблюдение основного массива. При выборочном наблюдении единицы исследуемой совокупности выбираются методом случайного отбора. Наблюдение основного массива – исследование определенных наиболее существенных по значимости изучаемых признаков единиц совокупности. Монографическое наблюдение – глубокое и всестороннее исследование лишь отдельных единиц совокупности, обладающих какими-либо специфическими особенностями.

2. в зависимости от временного фактора:

- непрерывное (текущее): осуществляется путем непрерывной регистрации фактов по мере их возникновения.

- прерывное: производится либо регулярно через определенные промежутки времени (периодическое), либо нерегулярно по мере надобности (единовременное).

3. в зависимости от источников сообщений:

- непосредственное: осуществляется путем фиксации фактов, лично установленных регистраторов в результате осмотра, измерения, подсчета признака изучаемого явления.

- документальное: в качестве источника информации используются данные различных документов.

- опрос: базируется на получении данных в форме ответов опрашиваемых лиц.

Способы наблюдения:

1. отчетный: все организации представляют в установленные сроки отчеты по определенной форме.

2. экспедиционный: состоит в том, сто к каждой единице наблюдения посылаются специальные лица, которые в специальных формулярах регистрируют сведения по наблюдаемым явлениям.

3. способ саморегистрации: характеризуется тем, что специальные работники снабжают опрашиваемых бланками и дают инструкции о порядке их заполнения.

4. анкетный: определенному кругу лиц выдаются анкеты, которые содержат вопросы. Анкеты могут публиковаться периодически. В отличие от способа саморегистрации заполнение анкет носит добровольный характер и осуществляется анонимно.