7. Линейная зависимость и линейная независимость векторов.

Набор векторов 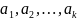называется системой вектроов

Система из k векторов называется линейно зависимой, если существуют такие числа 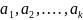, не все равные нулю одновременно, что:

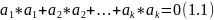
Систему из k векторов наз-ся линейно независимой, если равенство (1.1) возможно только при 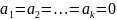, т. е. когда линейная комбинация в левой части равенства (1.1) тривеальная.

Замечание:

1.Один вектор a, тоже образует систему: при 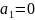– линейно зависимую, а при 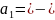линейно независимую.

2.Любая часть системы векторов называется подсистемой.

--Линейную комбинацию (1.1) векторов называют нетривеальной,, если хотя бы один из коэф-ов 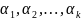отличен от нуля. В противном случае, линейную комбинацию (1.1) называют тривеальной.

--Семейство векторов содержащий нуль вектор линейно зависим.

Векторы a+b колинеарны тогда и только тогда, когда векторы a и b линейно зависимы.

Векторы a, b, c кол-ны, то a, b, с лигейно зависимы.

Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

.2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектор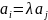а  , то она линейно зависима.

4. Система из 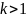  векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов 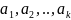  линейно независима, а после присоединения к ней вектора 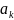  оказывается линейно зависимой, то вектор a можно разложить по векторам  , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

8. Векторное пространство. Координаты вектора.

Векторное пространство (линейное пространство) - множество элементов, называемых векторами, для которых определены операции сложения и умножения на число.

1)существуют семейства состоящие из n линейно не зависимых векторов.

2)всякое семейство из n плюс одного вектора линейно зависим.

(1-2) – называют аксиомами размерности.

--Векторное пространство V удовлетворяющее аксиомам (1-2) называют n-мерным 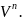Число n называют размерностью пространства .

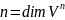--Всякий упорядоченный набор из n линейно независимых векторов пространства 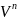называют базисом этого пространства. В пространстве может существовать бесконечное множество базисов.

--Если векторы базиса единственные и взаимно ортогональные то базис называют прямоугольным декартовым, в противном случае базис общий декартовый.

--Всякий вектор пространства можно представить в виде линейной комбинации базиса (разложить по векторам базиса) и притом единственным образом.

--Координатами вектора базиса называют коэффициенты его разложения по векторам этого базиса.

--Каждая координата линейной комбинации векторов равна точно такой же линейной комбинации (с теми же самыми коэффициентами) соответствующих координатам векторов линейной комбинации.

Следствия:

1)Каждая координата суммы 2-х векторов, равна сумме соответствующих координат векторов слагаемых

2)Каждая координата разности 2-х векторов, равна разности соответствующих координат уменьшаемого и вычитаемого векторов.

3)Каждая координата произведения вектора на число равна произведению соответствующей координаты данного вектора на данное число.

4)Коллинеарные векторы имеют пропорциональные соответствующие координаты. a=(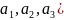 –координат вектора.