1. Определители и их свойства.

Определителем называется число, записанное в виде квадратной таблицы.

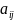. - элементы определителя (i – номер строки, j – номер столбца)

Основные определения:

Определители могут быть: 2-го порядка, 3-го порядка и др.

Порядком определителя называется число его строк и столбцов.

Минором 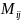к элементу называется определитель, полученный из исходного, вычеркиванием i-ой строки j-го столбца.

Алгебраическое дополнение

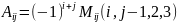
Основные свойства определителей:

1)Определитель не изменит своего значения, если его строки поменять местами с соответствующими столбцами.

2)При перестановке 2-х каких либо рядов определитель меняет лишь знак.

3)Определитель с двумя одинаковыми рядами равен нулю.

4)Множитель, общий для элементов какого-либо ряда, можно вывести за знак определителя.

5)Определитель, у которого все элементы какого-либо ряда равны нулю, то сам равен нулю.

6)Определитель с двумя пропорциональными рядами равен нулю.

7)Определитель равен сумме произведений элементов некоторого ряда на их алгебраические дополнения.

8)Определитель, не изменит своего значения, если к элементам некоторого ряда прибавить элементы другого нар-го ему ряда, умноженные на одно и то же число.

2. Матрицы. Основные определения. Линейные операции над матрицами. Умножение матриц.

Матрицей размера 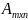называется прямоугольная таблица чисел, содержащая m строк и n столбцов. (i=1, m. j-1, n.)

Вектор - строкой называют матрицу, состоящую из одной строки.

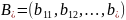
Вектор – столбцом – из одного столбца.

-Матрицу, у которой количество столбцов равно количеству строк, называется квадратной матрицей n-го порядка.

-Порядком квадратной матицы, называют число его строк или столбцов.

-Квадратную матрицу А называют симметричной, если элементы матрицы симметричные относительно его главной диагонали равны.

-Квадратную матрицу называют диагональной, если все его элементы не расположенные на главной диагонали равны 0 (D = (….)).

-Если у диагональной матрицы n-го порядка на главной диагонали все элементы равны 1, то матрица называется единичной и обозначается Е.

-Матрицу любого размера, все элементы которой равны 0, то называется нуль – матрицей.

Линейные операции над матрицами:

-сложение

-вычитание

-умножение матрицы на число

Свойств операции сложения и умножения на число.

1)А+В = В+А (коммутативность)

2)(А+И)+С = А+(В+С) (ассоциативность)

3)А+0 = А

4)(-А)+А = 0

Умножение матриц.

Матрицу 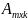называют согласованной с матрицей 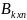, если число столбцов матрицы А, равны числу строк матрицы В.

Определитель произведения 2-х матриц равен произведению их определителей.

А-> defA, det(A*B) = defA*detB

detA – определитель.

3. Обратная матрица. Матричный способ решения n линейных уравнений с n неизвестными.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

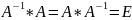
Квадратная матрица А называется невырожденной или неособенной, если ее определитель отличен от нуля, и вырожденной, или особой, если дельта = 0.

Нахождение обратной матрицы:

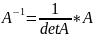
Свойства обратной матрицы:

1)

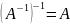
2)

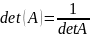
3)

Обратная матрица может существовать только для квадратной вырожденной матрицы А.

-Минором к-го порядка матрицы А наз-ют определитель состоящий на пересечении каких либо к строк и к-столбцов этой матрицы.

-Рангом матрицы А называют наибольший порядок отличных от нуля миноров этой матрицы.

-Матрицу полученную из данной с помощью конечного числа эл-ых преобразований наз-ют экв-ой к заданной.

--при переходе от данной матрицы к эквивалентной ранг матрица не изм-ся. Минор матрицы порядок которого определяет ее ранг наз-ют базисным. Ранг матрицы можно найти, например, методом эл-ых преобразований или методом окаймляющих миноров.

СЛУ: решение системы линейных алгебраических уравнений по матричному методу определяется равенством 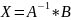 . Другими словами, решение СЛАУ находится с помощью обратной матрицы  .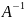

Систему n линейных алгебраических уравнений с n неизвестными можно решать матричным методом только тогда, когда определитель основой матрицы системы отличен от нуля.