7. Охарактеризуйте теоретичні аспекти та практичні підходи до реалізації наступних алгоритмів сортування даних у нелінійних структурах: турнірне сортування.

Цей метод сортування отримав свою назву через схожість з кубковою системою проведення спортивних змагань: учасники змагань розбиваються на пари, в яких розігрується перший тур; з переможців першого туру складаються пари для розиграшу другого туру і т.д. Алгоритм сортування складається з двох етапів. На першому етапі будується дерево: аналогічне схемі розиграшу кубка.

В примере 3.12 приведена программная иллюстрация алгоритма турнирной сортировки. Она нуждается в некоторых пояснениях. Построение пирамиды выполняется функцией Create_Heap. Пирамида строится от основания к вершине. Элементы, составляющие каждый уровень, связываются в линейный список, поэтому каждый узел дерева помимо обычных указателей на потомков - left и right - содержит и указатель на "брата" - next. При работе с каждым уровнем указатель содержит начальный адрес списка элементов в данном уровне. В первой фазе строится линейный список для нижнего уровня пирамиды, в элементы которого заносятся ключи из исходной последовательности. Следующий цикл while в каждой своей итерации надстраивает следующий уровень пирамиды. Условием завершения этого цикла является получение списка, состоящего из единственного элемента, то есть, вершины пирамиды. Построение очередного уровня состоит в попарном переборе элементов списка, составляющего предыдущий (нижний) уровень. В новый уровень переносится наименьшее значение ключа из каждой пары. 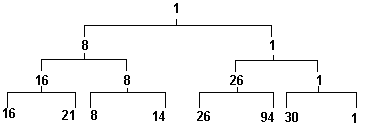Рис.3.13. Пирамида турнирной сортировки Следующий этап состоит в выборке значений из пирамиды и формирования из них упорядоченной последовательности (процедура Heap_Sort и функция Competit). В каждой итерации цикла процедуры Heap_Sort выбирается значение из вершины пирамиды - это наименьшее из имеющихся в пирамиде значений ключа. Узел-вершина при этом освобождается, освобождаются также и все узлы, занимаемые выбранным значением на более низких уровнях пирамиды. За освободившиеся узлы устраивается (снизу вверх) состязание между их потомками. Так, для пирамиды, исходное состояние которой было показано на рис 3. , при выборке первых трех ключей (1, 8, 14) пирамида будет последовательно принимать вид, показанный на рис.3.14 (символом x помечены пустые места в пирамиде). Рис.3.14. Пирамида после последовательных выборок Процедура Heap_Sort получает входной параметр ph - указатель на вершину пирамиды. и формирует выходной параметр a - упорядоченный массив чисел. Вся процедура Heap_Sort состоит из цикла, в каждой итерации которого значение из вершины переносится в массив a, а затем вызывается функция Competit, которая обеспечивает реорганизацию пирамиды в связи с удалением значения из вершины. Функция Competet рекурсивная, ее параметром является указатель на вершину того поддерева, которое подлежит реорганизации. В первой фазе функции устанавливается, есть ли у узла, составляющего вершину заданного поддерева, потомок, значение данных в котором совпадает со значением данных в вершине. Если такой потомок есть, то функция Competit вызывает сама себя для реорганизации того поддерева, вершиной которого является обнаруженный потомок. После реорганизации адрес потомка в узле заменяется тем адресом, который вернул рекурсивный вызов Competit. Если после реорганизации оказывается, что у узла нет потомков (или он не имел потомков с самого начала), то узел уничтожается и функция возвращает пустой указатель. Если же у узла еще остаются потомки, то в поле данных узла заносится значение данных из того потомка, в котором это значение наименьшее, и функция возвращает прежний адрес узла.