19. Преобразователи линейных и угловых перемещений в цифровой код. Устройство и принцип действия преобразователей. Схемы включения в цепь. Коды Грея. Оптоэлектронные пары.

В случае измерения линейных и угловых перемещений объекта измерения можно создать преобразователь, преобразовывающий его положение (линейное или угловое) в пространстве в цифровой код.

1.2.1 Абсолютные цифровые преобразователи

Абсолютные цифровые преобразователи - это рейки для линейных перемещений или диски для угловых перемещений, разделенные на N равновеликих площадок (полос в случае рейки, секторов в случае диска), на которых записаны бинарные слова, соответствующие определяемому положению рейки или диска согласно цифровому коду и конкретной технологии. Число площадок N определяет разрешение следующим образом: L/N см для рейки длиной L см и 360°/N для диска.

Все n бит, образующие каждое из слов, материализуются на n параллельных (для рейки) или концентрических (для диска) дорожках. Их схематическое изображение приведено на рисунках 1.19 и 1.20. Для определения логических значений

0 -
000000 или 1
1 -

могут быть использованы различные физические состояния носителей измерительной информации:

- ненамагничиваемая или ферромагнитная поверхность (магнитное считывание);

- изолирующая или проводящая поверхность (электрическое считывание);

- непрозрачная и просвечивающая поверхность (оптическое считывание).

В настоящее время оптическое считывание применяется наиболее часто; для каждой дорожки имеется источник – светодиодный преобразователь и приемник-фототранзистор (рисунок 1.21).

Кодирование. Прямой двоичный код можно использовать с помощью такого обрабатывающего прибора, как вычислитель.

Наиболее часто применяют код Грея, для которого коды, отличающиеся на единицу в десятичной системе, различаются только в одном разряде двоичной системы. Погрешность считывания таких кодов не превышает 1.

Цифры разряда кодов Грея не имеют определенного веса, что затрудняет вычисления, поэтому код Грея переводится в двоичный код. Правило перевода следующее: код Грея получается из двоичного кода путем суммирования с данным двоичным разрядом этого же числа, но сдвинутого на один разряд в сторону младшего разряда и без переноса в процессе сложения 1 в следующий разряд.

Характеристики преобразователя «угол - код». Основные метрологические характеристики преобразователя следующие:

- число разрядов выходного кода - n;

- квант по уровню q (или значение единицы младшего разряда кода) определяется значением 360°/2ⁿ;

- разрешающая способность - максимальное изменение угла, которое не приводит к изменению выходного кода, - определяется квантом по уровню и равно значению q;

- предельное значение допускаемой основной абсолютной погрешности преобразователя - максимальное значение разности результата измерения угла Nq и действительного значения угла .

Квантование по уровню для преобразователя «угол - код». Преобразователь «угол - код» реализует метод считывания при преобразовании аналоговой величины в код, при котором текущее значение угла сравнивается с квантованной шкалой значений угла. При квантовании угла (замене значения угла квантованным значением) возможны два способа отождествления:

- с ближайшим меньшим квантованным значением;

- с ближайшим квантованным значением.

При первом способе отождествления начала квантованной шкалы и шкалы значений угла совпадают.

Второй способ отождествления реализуется смещением начала квантованной шкалы на половину кванта относительно шкалы значений угла, для чего кодирующий диск повернут на угол q/2 относительно нулевого значения угла.

Характеристики погрешности квантования. Если N - выходной код измерительного преобразователя, a q - квант по уровню, то измеренное значение угла равно _и = Nq. Текущее значение абсолютной погрешности квантования угла равно _кв = _и -  = Nq - .

В общем случае погрешность квантования можно рассматривать как случайную равномерно распределенную величину, при этом для первого способа квантования значения _кв лежат в интервале [-q; 0], для второго способа квантования значения погрешности лежат в интервале [-q/2; +q/2].

В качестве характеристик погрешности применяются следующие:

- предельные значения погрешности (границы, в которых может находиться погрешность), задаваемой нижними и верхними границами;

- вероятностные характеристики погрешности в виде плотности вероятности или числовых характеристик погрешности: математического ожидания, дисперсии, среднеквадратичного отклонения погрешности (корень квадратный из дисперсии), доверительных интервала и вероятности для погрешности.

Для первого способа квантования нижнее предельное значение погрешности равно -q, верхнее - 0, а вероятностные числовые характеристики погрешности квантования - математическое ожидание m_кв = =- q/2; дисперсия D_кв = q²/12; среднее квадратическое отклонение  = q/2 . Наличие математического ожидания погрешности для первого способа квантования по уровню свидетельствует о наличии систематической составляющей погрешности измерения.

Для второго способа квантования предельные значения погрешности квантования равны ± q/2, а вероятностные числовые характеристики погрешности квантования те же, что и у первого способа, за исключением математического ожидания, равного нулю.

20. Измерительные преобразователи частоты в цифровой код. Устрой­ство и принцип действия, временные диаграммы работы преобразователей. Основные метрологические характеристики и оценка погрешности преобразо­вания.

Р азличают преобразователи, измеряющие частоту f_Х за один период колебаний T_Х, и преобразователи средних значений, измеряющие частоту f_Х путем подсчета числа периодов T_Х за интервал времени измерения T_И > T_Х и деления полученного числа на T_И.

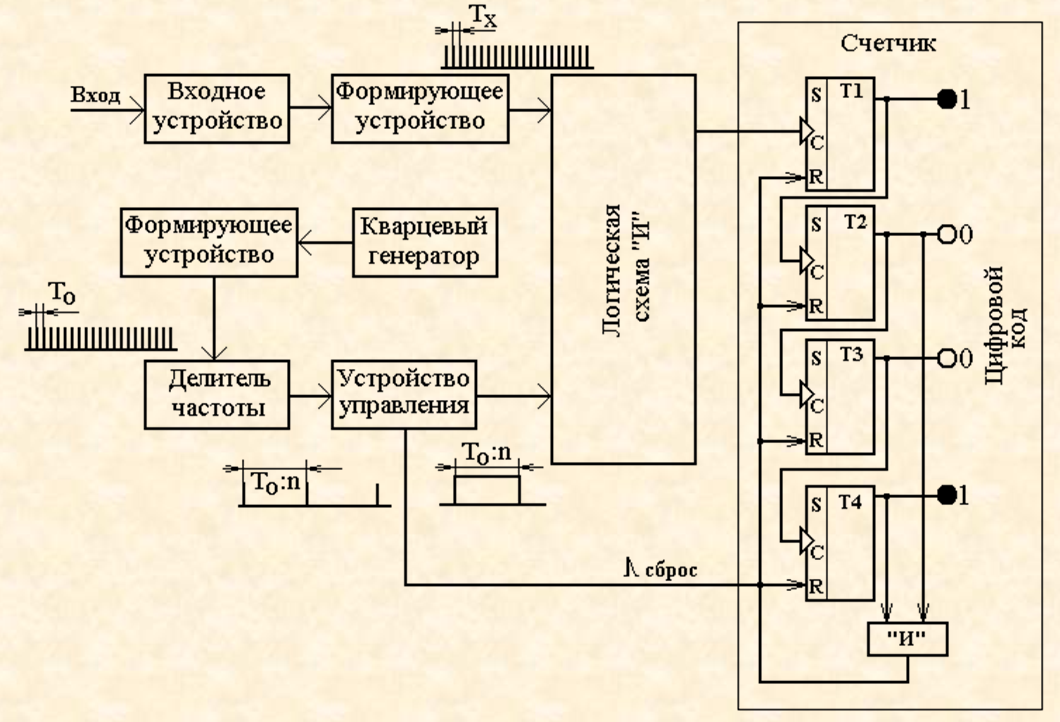
Таким образом, счетчик фиксирует число импульсов N (диаграмма U₄), связанное с T_Х и T_И очевидным соотношением

Т_И = N T_Х, откуда f_Х =

Относительная погрешность преобразования Fx:

,

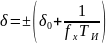где