Билет 11. 1)Рассмотрим дифференциальное уравнение вынужденных колебаний (1)

.

Согласно теореме о структуре общего решения неоднородного линейного уравнения все движения, определяемые уравнением (1), складываются из совокупности всех движений, определяемых соответствующим однородным уравнением и называемых собственными колебаниями точки, и какого-нибудь однородного движения, определяемого неоднородным уравнением (1).

Как было отмечено, все колебания, определяемые уравнением (1), всегда можно найти методом вариации произвольных постоянных.

Если правая часть уравнения (1) имеет специальный вид, позволяющий найти частное решение методом неопределенных коэффициентов, то метод Лагранжа применять не следует.

совпадение частоты возмущающей силы с частотой собственных колебаний (резонанс). несовпадение этих частот (нерезонансный случай).

Явление резонанса находит широкое применение в технике. Так, для уплотнения сыпучего основания под фундаменты и дороги, а также для уплотнения бетона используют специальные вибраторы-уплотнители.

2) Работа силы - количественная мера превращения механического движения в другие виды движения.

Если сила постоянна по модулю и направлению, а точка ее приложения перемещается прямолинейно, то работа равна произведению модуля силы, длинны перемещения и косинуса угла между этими векторами: . Знак работы совпадает со знаком проекции силы на ось перемещения.

Мощность - работа, выполненная за единицу времени.

Теорема о работе равнодействующей силы: работа равнодействующей на некотором перемещении равна алгебраической сумме работ, составляющих ее сил на этом же перемещении.

Работа сил тяжести, упругости.

Работа силы тяжести численно равна произведению силы тяжести на вертикальное перемещение точки ее приложения, не зависит от траектории перемещения, а только от расстояние между вертикальными проекциями начального и конечного положения точки:

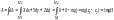
Работа силы упругости численно равна произведению половины коэффициента жесткости на квадрат перемещения точки приложения силы, поскольку модуль силы упругости равен произведению коэффициента жесткости на удлинение:

.

Билет 12.

Работа силы. Мощность. Элементарная работа dA = Ftds, Ft – проекция силы на касательную к траектории, направленная в сторону перемещения, или dA = Fdscosa.

Если a – острый, то dA>0, тупой – <0, a=90o: dA=0. dA= – скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= Fxdx+Fydy+Fzdz – аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М0М1: . Если сила постоянна, то = F×s×cosa. Единицы работы:[1 Дж (джоуль) = 1 Нм].

, т.к. dx= dt и т.д., то .

Теорема о работе силы: Работа равнодействующей силы равна алгебраической сумме работ составляющих сил на том же перемещении А=А1+А2+…+Аn.

Работа силы тяжести: , >0, если начальная точка выше конечной.

Работа силы упругости: –работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.

Работа силы трения: если сила трения const, то - всегда отрицательна, Fтр=fN, f – коэфф.трения, N – нормальная реакция поверхности.

Работа силы тяготения. Сила притяжения (тяготения): , из mg= , находим коэфф. k=gR2. – не зависит от траектории.

Мощность – величина, определяющая работу в единицу времени, . Если изменение работы происходит равномерно, то мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) =

= 1000 Вт, 1л.с.(лошадиная сила) = 75 кгс×м/с = 736 Вт].

Билет 13

1) Непнерииальные системы отсчета (нсо)

Определение: Неинерпиальной системой отсчета (НСО) называется система, движущаяся ускоренно относительно инерцнальной (ИСО). Простейшие НСО - это системы, движущиеся ускоренно прямолинейно, и системы врашаюшиеся. Задача состоит в том. чтобы найти уравнения движения в НСО. эта задача сводится к установлению законов преобразования сил и ускорений при переходе от ИСО к НСО

Условимся считать произвольно выбранную ИСО неподвижной, а движение относительно нее абсолютным. Если тело неподвижно в системе отсчета, которая движется относительно выбранной ИСО. то такое движение тела назовем переносным.

Движение тела относительно движущейся системы отсчета назовем относительным.

2)Работа внутренних сил

Внутренние силы - силы взаимодействия точек системы. Свойства внутренних сил:

1. главный вектор внутренних сил равен нулю;

2. главный вектор момент внутренних сил относительно любого неподвижного центра равен нулю

Твёрдое тело есть совокупность материальных точек, рассотяние между которыми не изменяется. Если рассмотреть все точки и векторно сложить все силы взаимодействия, то получим 0. Раз результирующая сила нулевая, то и работы она не совершает.

Работа сил, приложенных к твердому телу.

Работа внутренних сил на конечном перемещении равна нулю.

Работа силы, действующей на поступательно движущееся тело равна произведению этой силы на приращение линейного перемещения.

Работа силы, действующей на вращающееся тело равна произведению момента этой силы относительно оси вращения на приращение угла поворота: ; .

Затухающие колебания мат. точки

Затухающие колебания происходят в том случае, когда на точку, кроме восстанавливающей силы действует сила сопротивления.

R=-µv µ - коэффициент сопротивления среды

– диф. уравнение затухающих колебаний

n= - частота затухающих колебаний

Билет 14. 1) Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.

Теорема Гюйгенса-Штейнера

Согласно теореме Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

Гироско́п— устройство, способное реагировать на изменение углов ориентации связанного с ним тела относительно инерциальной системы координат, как правило, основанное на законе сохранения вращательного момента

Классификация: Основные типы гироскопов по количеству степеней свободы:-2-степенные (интегрирующие, дважды интегрирующие, дифференцирующие)-3-степенные.Основные два типа гироскопов по принципу действия:-механические гироскопы,-оптические гироскопы.

По режиму действия гироскопы делятся на:

-датчики угловой скорости,

-указатели направления.

Однако одно и то же устройство может работать в разных режимах в зависимости от типа управления.