2.3. Текущая стоимость

Как мы уже выяснили, сегодняшние деньги стоят дороже, чем будущие. Если нам предлагают купить бескупонную облигацию, а через год обещают эту ценную бумагу погасить и выплатить 1000 р., то необходимо определить цену данной облигации, по которой мы согласились бы ее купить. По сути дела, для нас задача сводит­ся к определению текущей стоимости 1000 р., которая возникает через год.

Текущая стоимость — это дисконтированная стоимость буду­щего денежного потока. Она является своего рода оборотной сто­роной будущей стоимости. Ее можно рассчитать по формуле опре­деления будущей стоимости

где PV— текущая стоимость; FV — будущая стоимость; r — ставка

дисконтирования;

- коэффициент дисконтирования.

1

В приведенном ранее примере мы можем определить цену об­лигации, пользуясь данной формулой. Для этого нужно знать ставку дисконтирования. В качестве ставки дисконтирования берут до­ходность, которую можно получить на финансовом рынке, вкла­дывая деньги в какой-либо финансовый инструмент с аналогич­ным уровнем риска (банковский депозит, вексель и т.п.). Если у нас есть возможность разместить деньги в банке, который выпла­чивает за год 15 %, то цена предлагаемой нам облигации равна

Таким образом, купив данную облигацию за 869 р. и получив через год при ее погашении 1000 р., мы заработаем 15%.

Пример. Инвестору требуется определить, какую сумму ему нуж­но разместить на банковском депозите, чтобы через 4 года получить в банке сумму равную 15 000 долл., при рыночных валютных ставках 12 % годовых?

Для определения приведенной стоимости целесообразно пользо­ваться таблицами дисконтирования, отражающими текущую сто­имость денежной единицы, которую предполагается получить че­рез несколько лет (табл. 2.4).

Пример. Требуется определить приведенную стоимость 500 долл., которые предполагается получить через 7 лет при ставке дисконтирова­ния, равной 6 %. В таблице на пересечении строки «7 лет» и столбца «6 %» находим коэффициент дисконтирования, который равен 0,665. В этом слу­чае приведенная стоимость 500 долл. будет равна 500 • 0,665 = 332,5 долл.

Если проценты выплачивать чаще, чем один раз в год, то фор­мула определения текущей стоимости модифицируется аналогич­но тому, как мы поступали с расчетами будущей стоимости. При многократном начислении процентов в течение года формула оп­ределения текущей стоимости имеет вид

.

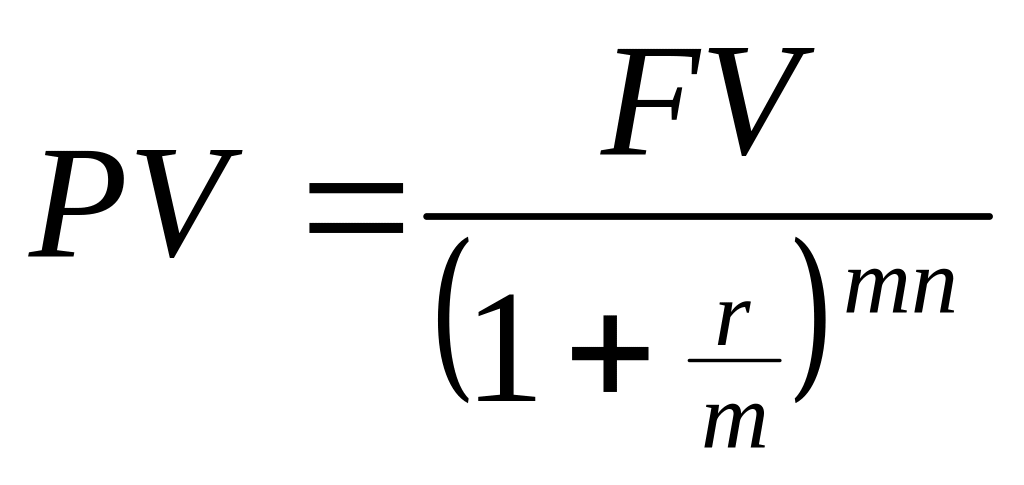Таблица 2.4.

Приведенная стоимость денежной единицы, которая будет получена через п лет

Коли­чество лет	Годовая процентная ставка %
	1	2	…	5	6	…	10	…	15
1	0,990	0,980	…	0,952	0,943	…	0,909	…	0,870
2	0,980	0,961	…	0,907	0,890	…	0,826	…	0,756
3	0,971	0,942	…	0,864	0,840	…	0,751	…	0,658
4	0,961	0,924	…	0,823	0,792	…	0,683	…	0,572
5	0,951	0,906	…	0,784	0,747	…	0,621	…	0,497
6	0,942	0,888	…	0,746	0,705	…	0,564	…	0,432
7	0,933	0,871	…	0,711	0,665	…	0,513	…	0,376
…	…	…	…	…	…	…	…	…	…
10	0,905	0,820	…	0,614	0,558	…	0,386	…	0,247
…	…	…	…	…	…	…	…	…	…
15	0,861	0,743	…	0,481	0,417	…	0,239	…	0,123
…	…	…	…	…	…	…	…	…	…
20	0,820	0,673	…	0,377	0,312	…	0,149	…	0,061

В рассмотренном примере с четырехлетним депозитом предположим, что проценты по вкладу начисляются ежеквартально. В этом случае, что­бы иметь через четыре года 15 000 долл., инвестор должен разместить на депозите сумму, равную

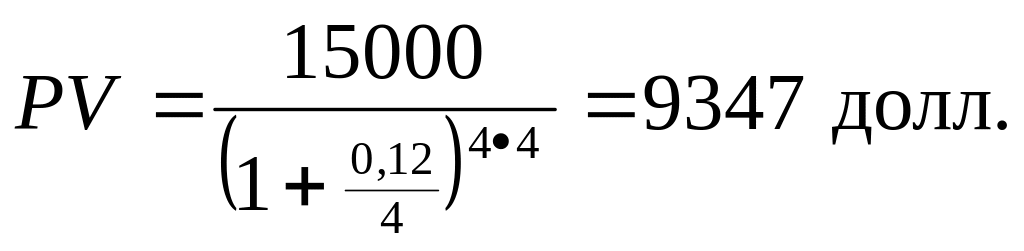
Таким образом, чем чаще начисляются проценты, тем меньше текущая стоимость при заданном конечном результате, т.е. взаи­мосвязь между частотой начисления процентов и текущей сто­имостью обратна по сравнению с той, которая складывается для будущей стоимости.

В практической деятельности финансовые менеджеры посто­янно сталкиваются с проблемой выбора вариантов, когда необхо­димо сравнивать разновременные денежные потоки.

Пример. Существует два варианта финансирования строительства нового объекта. Общий срок строительства составляет 4 года, его смет­ная стоимость — 10 млн. р. В конкурсе на получение подряда участвуют организации А и В, которые предлагают следующие условия оплаты ра­бот по годам (табл. 2.5).

Таблица 2.5.