Будущая стоимость денежной единицы

Коли­чество лет	Годовая процентная ставка, %
	1	2	…	5	6	…	10	15
1	1,010	1,020	…	1,050	1,060	…	1,100	1,150
2	1,020	1,040	…	1,102	1,124	…	1,210	1,323
3	1,030	1,061	…	1,158	1,191	…	1,331	1,521
4	1,041	1,082	…	1,216	1,262	…	1,464	1,749
5	1,051	1,104	…	1,276	1,338	…	1,611	2,011
…	…	…	…	…	…	…	…	…
10	1,105	1,219	…	1,629	1,791	…	2,594	4,046
…	…	…	…	…	…	…	…	…
15	1,161	1,346	…	2,079	2,397	…	4,177	8,137
…	…	…	…	…	…	…	…	…
20	1,220	1,486	…	2,653	3,207	…	6,727	16,37

Пример. Пользуясь данной таблицей, определим, сколько денег бу­дет на счете инвестора, который положил 1000 р. на банковский депозит под 10% сроком на 15 лет. Мы движемся вниз по столбцу «Количество лет» до строки 15 лет, а затем перемещаемся по этой строке вправо до столбца «10 %». На пересечении строки и столбца показана сумма, во что превратится 1 р. через 15 лет, положенный на депозит под 10% годовых. Эта цифра равна 4,177. Следовательно, для нашего примера будущая сто­имость вклада равна

FV= 1000 · 4,177 = 4177 р.

На рис. 2.3 представлена динамика изменения первоначального вклада при простом и сложном начислении процентов.

При простом проценте увеличение стоимости происходит рав­номерно. При сложном проценте наблюдается ускоренный рост накоплений. Кривая роста тем круче, чем выше ставка процента и продолжительнее срок инвестирования.

Кроме годового начисления процентов, встречаются формы инвестиций (вкладов), по которым проценты начисляются не­сколько раз в течение года. В этом случае будущая стоимость рас­считывается по формуле

где m — количество периодов начисления процентов в течение года, n — количество лет.

Пример. Инвестор разместил 100 р. на банковском депозите сроком на 1 год, но условиями договора предусмотрено, что начисление процен­тов осуществляется по полугодиям. Если годовая процентная ставка со­ставляет 15 %, то за 6 мес. начисляется 7,5 %. Будущая стоимость годового депозита в данном случае составит FV= 100(1 + 0,15/2)² = 115,56 р.

Если выплаты производятся несколько раз в течение года, то реальный процент получается больше, чем номинальная процентная ставка.

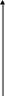
Стоимость, р.

0 годы

рис. 2.3. Рост стоимости при простом и сложном проценте:

1,2- сложный процент, соответственно 15 и 10%; 3- простой процент

Таблица 2.3

Номинальные процентные ставки и эффективные проценты

Число выплат в году	Номинальная процентная ставка, %
	5	10	15	20
1	5,00	10,00	15,00	20,00
2	5,06	10,25	15,56	21,00
4	5,09	10,38	15,87	21,55
12	5,12	10,47	15,08	21,94
365	5,13	10,52	16,18	22,13

В табл. 2.3 приведены номинальные процентные ставки и реальные (эффективные) проценты.

Из табл. 2.3 видно, что если выплаты производятся один раз в год, то номинальная процентная ставка, указанная в договоре, равна эффективному проценту. Если же проценты начисляются несколько раз в году, то эффективный процент больше номи­нальной процентной ставки. Например, согласно договору годо­вая процентная ставка составляет 15%, а начисление процен­тов осуществляется ежеквартально. Следовательно, фактически через год инвестор заработает 15,87 %. Допустим при этом, что банк предлагает два варианта размещения средств на депозите: 15,5 % с выплатой раз в год и 15 % с ежеквартальным начисле­нием процентов. Второй вариант более выгоден, так как факти­ческая доходность составит 15,87 %. Итак, чем чаще осуществ­ляется начисление процентов в течение года, тем выше факти­ческая доходность по сравнению с номинальной. Поэтому при инвестировании средств необходимо учитывать частоту процен­тных выплат.