6.4. Доходность и оценка акций

Приобретая акции того или иного эмитента, инвестор предпо­лагает получить доход от своих вложений, который имеет две формы: дивиденды и прирост курсовой стоимости акций. При рас­чете доходности акций необходимо различать текущую доходность и полную доходность. Текущая (дивидендная) доходность характе­ризуется размером годовых дивидендных выплат, отнесенных к цене акции. Например, инвестор приобрел акцию по цене 10 р. По итогам года на нее был выплачен дивиденд в размере 1 р. Ди­видендная доходность составила 10 %. Она является одним из по­казателей, характеризующих финансовые результаты деятельности компании. Его учитывают инвесторы при принятии решения о по­купке акций. Приобретая акции инвестор на основе данных о вып­лате дивидендов за предыдущие годы и анализа текущего финансо­вого состояния оценивает возможные дивидендные выплаты теку­щего года и рассчитывает ожидаемую дивидендную доходность. Однако ожидания инвестора могут не оправдаться. Ведь реальный размер дивидендов определяет общее собрание акционеров. В этом случае фактическую дивидендную доходность можно рассчитать путем сопоставления размера объявленных дивидендов с ценой акций на дату составления списка акционеров, имеющих право на

получение дивидендов.

Но, как уже говорилось, получаемые дивиденды — это только часть дохода от владения акциями, причем зачастую не самая боль шая. Большую часть дохода составляет прирост курсовой стоимо­сти акций. В отличие от облигаций за акциями стоят реальные активы фирмы, и это отражается на их рыночной цене. В случае успешного развития предприятия увеличиваются его активы, ра­стет стоимость акций. Поэтому инвестор, вкладывая свои средства в акции, рассчитывает не столько на получение текущего дохода, сколько на получение совокупного дохода, учитывающего рост курсовой стоимости акций.

Полная доходность характеризуется размером выплачиваемых дивидендов и приростом цены акций по отношению к вложенно­му капиталу. Если средняя цена акции составляет Р_о, а ожидаемая цена через год Р₁ причем за этот год будут выплачены дивиденды (d₁), то полную годовую доходность (Дn) можно определить как

Дn = d1+(Pо-P1)/Pо*100

Рассчитаем ожидаемую доходность акций, которые в настоя­щее время стоят 100 р., если через год предполагается повышение цены акции до 115 р., а по итогам истекшего года будет выплачен дивиденд в размере 5 р. на акцию. Ожидаемая полная доходность акционера составит

Дn = 5+(115-100)/100 = 0,2, или 20%.

Выгодно ли инвесторам покупать акции данной компании? Если акции аналогичных компаний с таким же уровнем риска прино­сят годовую доходность в размере 20 %, то имеет смысл приобре­тать данные акции. Чтобы определить приемлемую цену покупки, необходимо сделать прогноз будущей стоимости акций (Р1) и ожидаемых дивидендов (d₁). В этом случае сегодняшнюю цену ак­ций можно определить по формуле

Po=(d1+P1)/(1+r)

где r — ставка дисконтирования.

В нашем примере ожидаемые дивиденды составляют 5 р., цена акции через год равна 115 р., а норма доходности по акциям с аналогичным уровнем риска достигает 20 %. Следовательно, приемлемая цена покупки акции

_{Po=(5+115)/(1+0,2)=100 р.}

Рассчитанная таким путем цена показывает верхний предел цены акций для инвесторов, ориентирующихся на приобретение ценных бумаг с данным уровнем риска. Если акции данной компании на ранке будут стоить дешевле 100 р., то инвестору целесообразно эти акции приобрести. Ведь в случае достижения прогнозных показателей по дивидендам и цене акции через год он получит доходность от своих вложений более 20%. Если же цена акции окажется выше 100 р., то ожидаемая доходность через год будет меньше 20%. В этом случае лучше поискать на рынке другие финансовые инструменты с аналогичным риском, которые обеспечивают 20%-ную доходность.

Расчет текущей цены (Р_о) базируется на ожидаемой цене ак­ции через год (Р₁). Чем же определяется цена акции будущего года? Если руководствоваться формулой определения цены акции теку­щего года, которая верна для текущего дня, и использовать ее для определения цены акции через год, то можно записать

P1 = (d2+P2)/(1+r)

где d2 — дивиденды на акцию во вторим году; Р2 — цена акции в конце второго года; r — ожидаемая норма доходности(ставка дисконтирования).

Вполне логично предположить, что через год инвестора будут интересовать дивиденды следующего года и цена акции в конце его. Таким образом, можно определить текущую цену акции, ис­пользуя вышеприведенные формулы

Po = (d1+P1)/(1+r)=(d1/1+r)+(P1/1+r)

Подставляя вместо Р1 формулу расчета данного показателя, получим

Po = (d1/1+r)+(d2+P2/(1+r)²)

Если через два года ожидается, что цена акции составит 132,25 р., а дивиденды во втором году будут равны 5,75 р., то сегодняшняя цена акции составит

Po = 5/1,2+(5,75+132,25)/1,2² = 100 р.

Используя данный алгоритм, можно определить Р₂ через ожи­даемые дивиденды третьего года. Затем определить Р₃ и т.д. Тогда в общем виде формулу расчета акций в настоящий момент можно представить в следующем виде:

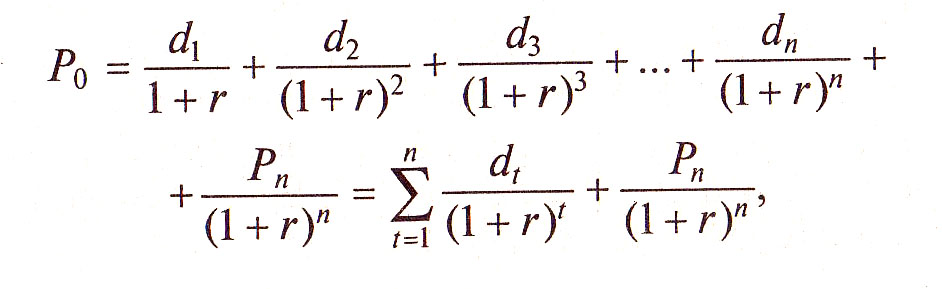
где dt – дивиденды в t-м году; Pn – цена акции в n-м году; r – ожидаемая норма доходности; t=1,…n – порядковый номер года.

На неограниченном временном горизонте (компания в идеале может существовать вечно) приведенная стоимость акции стремится к нулю, поскольку выражение Pn/(1+r)ⁿ при n→∞ будет бес­конечно малой величиной, которой можно пренебречь. В этом слу­чае формулу определения текущей цены акции мы можем запи­сать в следующем виде:

Po = ∑ dt/(1+rд)

Если величина дивидендов не меняется по годам, то мы имеем регулярный одинаковый денежный поток в течение бессрочного периода времени, который называется рентой. Но текущая сто­имость бессрочной ренты равна сумме годовых поступлений, де­ленной на ставку дисконтирования.

Рассмотрим пример по компании, которая по акциям ежегод­но выплачивает равновеликий дивиденд в размере 10 р. Если тре­буемая доходность (ставка дисконтирования) равна 20 %, то те­кущая цена этой акции составит

Po = d/r = 10/0,2 = 50 р.

Такой подход к определению стоимости применяется для при­вилегированных акций с фиксированной ставкой дивидендов. По обыкновенным акциям компании редко выплачивают неизмен­ные во все годы своего существования дивиденды.

Если компания развивается постоянными устойчивыми тем­пами, то можно предположить, что и дивиденды будут расти ана­логичным образом.

Попробуем рассчитать цену акции компании ABC, если в пер­вый год выплачиваются дивиденды в размере 5 р., а дивиденды и курсовая стоимость акции ежегодно увеличиваются на 10 %. Ожида­емый уровень доходности равен 15 %. Расчет представлен в таблице.

При расчете использовалась формула

Po = ∑ dt/(1+r)+Pn/(1+r)ⁿ

Пример. Рассчитаем текущую цену акции на основе прогнозных зна­чений ее цены и дивидендов на ближайшие четыре года:

Po = 5/(1+0,15)+5,5/1,15²+6,05/1,15³+6,66/1,15^4+146,6/1,15^4 = 100