1.2 Формализация и алгоритмизация задачи

В этом разделе требуется составить одну или несколько формул для решения приведенной ниже задачи. Для вычисления по этим формулам необходимо разработать программу, отражающую алгоритм линейного вычислительного процесса.

1. Выпуклый четырехугольник на плоскости задан координатами своих вершин. Найти его периметр.

2. Выпуклый четырехугольник на плоскости задан координатами своих вершин. Найти его площадь.

3. Треугольник на плоскости задан координатами своих вершин. Найти его периметр.

4. Треугольник на плоскости задан координатами своих вершин. Найти его площадь.

5. Две прямые на плоскости заданы своими направляющими векторами и точками. Найти их точку пересечения.

6. Две прямые на плоскости заданы своими нормалями и точками. Найти их точку пересечения.

7. Две прямые на плоскости заданы своими уравнениями. Найти их точку пересечения.

8. Вектор на плоскости задан координатами своих концов. Найти его направляющие косинусы.

9. Материальная точка движется по прямой траектории с постоянным ускорением. Известны ее координаты и скорость в начальный момент времени. Вычислить координату точки и ее скорость в заданный момент времени.

10. Две прямые на плоскости заданы своими двумя точками. Найти точку их пересечения.

11. Треугольник на плоскости задан координатами своих вершин. Найти длины его медиан.

12. Треугольник на плоскости задан координатами своих вершин. Найти координаты точки пересечения его медиан.

13. Треугольник на плоскости задан координатами своих вершин. Найти величины его углов.

14. Треугольник на плоскости задан координатами своих вершин. Найти длины его высот.

15. Треугольник на плоскости задан координатами своих вершин. Найти длину его средних линий.

16. Выпуклый четырехугольник на плоскости задан координатами своих вершин. Найти длины его диагоналей.

17. Две прямые на плоскости заданы двумя своими точками. Найти величину наименьшего угла, образованного этими прямыми.

18. Две прямые на плоскости заданы двумя своими точками. Найти координаты единичного вектора-биссектрисы наименьшего угла, образованного этими прямыми.

19. Прямоугольный треугольник задан двумя катетами. Вычислить периметр и площадь треугольника.

20. Вычислить площадь поверхности и объем шара с радиусом R.

21. Вычислить площадь поверхности и объем равнобедренной пирамиды, имеющей площадь основания S и высоту H.

22. Даны два круга с общим центром и радиусами. R₁ и R₂. Найти площади этих кругов, а также площадь кольца, внешний радиус которого равен R₁, а внутренний равен R₂.

23. Заданы координаты центра окружности радиуса R и координаты точки вне этой окружности, из которой проведены касательные к окружности. Найти расстояние от точки до точек касания.

24. Заданы координаты центра окружности радиуса R и координаты точки вне этой окружности, из которой проведены касательные к окружности. Найти площадь фигуры, ограниченной наибольшей дугой окружности и касательными.

25. Даны длины ребер прямоугольного параллелепипеда. Найти его объем и площадь поверхности.

26. Дана апофема тетраэдра и его высота. Найти периметр основания тетраэдра и площадь его боковой поверхности.

27. Дана сторона основания тетраэдра и его апофема (Апофема - длина перпендикуляра, опущенного из центра правильного многоугольника на одну из его сторон; апофема равна радиусу вписанного в данный многоугольник круга). Найти объем пирамиды.

28. Две окружности одинакового диаметра расположены на плоскости так, что расстояние между их центрами меньше диаметра. Найти площадь фигуры, ограниченной наибольшими дугами этих окружностей.

29. Две окружности одинакового диаметра расположены на плоскости так, что расстояние между их центрами меньше диаметра. Найти площадь области перекрытия.

30. Вычислить площадь фигуры изображенной на рис. 2.2 при заданных величинах r, а, c.

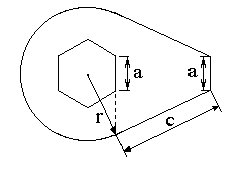
Рис. 2.2 Чертеж геометрической фигуры