5.2 Манипулирование фрагментами изображения

Этот метод использует набор дополнительных процедур. Для работы с фрагментом надо в первую очередь узнать его размер. Это делается с помощью функции:

S := ImageSize(xl, yl, x2, y2: integer): word;

где xl, yl и х2, у2 - координаты верхнего левого и правого нижнего угла прямоугольной области экрана. Функция возвращает размер S - указанного фрагмента в байтах.

Xранить образ фрагмента удобнее всего в динамической области памяти, поэтому результат работы ImageSize (например, величина S) часто являются входной информацией для процедуры GetMem, которая выделяет в динамической памяти указанный объем S по адресу P.

GetMem(VAR P: pointer; S: word);

Считывание образа прямоугольного фрагмента с экрана и сохранение в оперативной памяти компьютера выполняется процедурой

GetImage (xl, yl, x2, y2: integer; VAR BitMap);

где xl, yl, х2, у2 - координаты фрагмента, BitMap - не типизированный параметр, который долен быть больше или равен 6 плюс размер памяти, отведенный для области экрана. Первые два слова параметра BitMap определяют ширину и высоту области экрана, третье слово зарезервировано. Оставшаяся часть параметра BitMap используется для сохранения самого двоичного образа. Для определения размера памяти, необходимой для параметра BitMap, используют описанную выше функцию ImageSize.

Возвратить образ прямоугольного фрагмента из памяти на экран можно с помощью процедуры

PutImage (X,Y: integer; VAB BitMap; Mode: word);

где X, Y - координата точки экрана, начиная с которой будет выво­диться фрагмент; BitMap – описанный выше не типизированный параметр. Параметр Mode определяет, какой двоичный оператор будет использоваться для вывода двоичного образа области на экран и может принимать одно из следующих значений:

CONST CopyPut = 0; { операция MOV }

XORPut =1; { XOR }

ORPut =2; { OR }

AMDPut = 3; { AND }

NOTPut =4; { NOT }

Часто используют зарезервированную константу NomalPut, которая является аналогом пользовательской константы CopyPut. Каждая константа соответствует двоичной операции над пикселями фрагмента при его отображении на экране. Например, процедура

PutImage (X, Y, BitMap, NomalPut);

выводит на экран, начиная с точки X, Y, двоичный образ, сохраненный в массиве BitMap. Различные значения параметра Mode с комментариями приведены в табл. 3.6.

Таблица 3.6

Константа	Значение	Описание стиля заполнения
NomalPut	0	Сохраненная ранее область экрана полностью переопределяет предыдущее содержимое экрана.
XORPut	1	Код цвета пикселя в выводимой области образуется операцией исключающего ИЛИ кода цвета из буфера и кода цвета пикселя на экране.
ORPut	2	Код цвета пикселя в выводимой области образуется операцией логического ИЛИ кода цвета из буфера и кода цвета пикселя на экране.
ANDPut	3	Код цвета пикселя в выводимой области образуется операцией логического И кода цвета из буфера и кода цвета пикселя на экране.
NOTPut	4	Каждый бит кода цвета каждого пикселя в буфере логически инвертируется, после этого выводится на экран, полностью переопределяя его содержимое.

Отметим, что вывод фрагмента в режиме XOSPut обеспечивает его видимость на любом фоне. Повторный вывод того же самого фрагмента "стирает" окно, восстанавливая предыдущее содержание экрана. Вывод окна в режиме ANDPut, содержащего только белые и черные пиксели, приводит к тому, что пиксели выводимого окна черного цвета будут черными и на экране. Пиксели, имеющие белый цвет, не изменяют содержимого экрана. Режим полезен для "вырезания" из фона черного пятна произвольной формы. Это позволяет выводить на экран "непрозрачные" объекты, в том числе и при построении двигающихся изображений.

Для более ясного понимания техники манипулирования фрагментами рассмотрим следующий пример.

Пример 30. Составить программу для отображения на экране монитора диска диаметром в 5 пикселей, движущегося слева на право по синусоидальной траектории , где амплитуда синусоиды A = 40 пикселей, смещение вниз по оси ординат C = 90 пикселей, частота колебаний B = 0.1. После смещения диска следует оставлять траекторию движения его центра в виде последовательности точек (см. рис. 3.20).

Program PR30; {Программа движения диска со следом по синусоиде}

Uses Graph, CRT;

Var P1,P2:Pointer; {PI - указатель на образ "Следа",

Р2 - указатель на образ диска}

Grm, Grd, X, Y, X1, Y1: Integer; Size, C: Word;

Begin

Grd:=0; Initgraph(Grd, Grm, 'D:\Tp\Bgi'); {инициализация графического режима с автоматическим определением подходящего драйвера}

C := Getcolor; {С - текущий цвет изображения, белый}

X1 :=0; Y1 :=90; {XI,Y1 - начальные координаты диска}

Putpixel(X1,Y1+5,C); {Светящаяся точка - изображение "Следа"}

Size:= ImageSize(0,0,10,10); GetMem(P1,Size); {Size - количество

байтов для изображения квадрата 11*11}

Getimage(X1,Y1, X1+10,Y1+10,P1^); {P1 указывает на область

памяти с изображением следа}

Setfillstyle(11,C); {устанавливается тип и цвет закраски диска}

Circle(X1+5,Y1+5,5); {окружность с центром в X1,Y1}

Floodfill(X1+5,Y1+5,C); {заливка окружности}

Getmem(P2,Size); Getimage(X1, Y1, X1+10, Y1+10,P2^);

{Р2 указывает на область памяти с изображением диска}

For X:=1 TO 300

Do Begin

Y:= Trunc(40*Sin(0.1 *X)+90); {X, Y - графические координаты

нового положения диска}

Putimage(X1, Y1, P1^, 0); {на месте диска изображается след}

Putimage(X, Y, P2^, 0); {диск изображается на новом месте}

DELAY(100); {Частота вывода кадра - одна десятая секунды}

X1:=X; Y1:=Y; {Запоминаются старые координаты диска}

End;

Readln; {Ждем нажатия клавиши Enter}

CloseGraph

End.

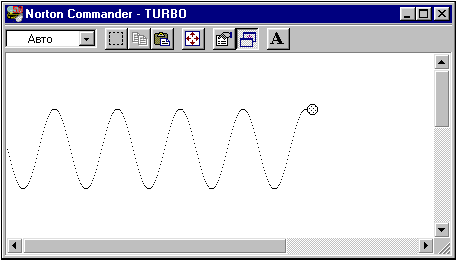
Рис. 3.20 Диск и след траектории его движения. На рисунке сделана инверсия цветов.

В приведенной выше программе скорость движения диска имеет две составляющие, первая - по оси X постоянная и принимает значение пикселей/сек. Величина - представляет собой суммарное время работы операторов в цикле программы, и зависит от характеристик процессора и монитора, на практике . Составляющая скорости по оси Y меняется по синусоидальному закону. С помощью траектории, отражающей положение центра диска на рис. 3.20 и размеров диска (радиус равен 5 пикселей) можно оценить диапазон изменения значение скорости пикселей/сек.

В следующей демонстрационной программе имитируется полет тарелки на фоне ночного замка (см. рис. 3.21). Летающая тарелка меняет случайным образом скорость своего движения в момент касания границ экрана. Это достигается изменением приращений dX и dY с помощью датчика случайных чисел.

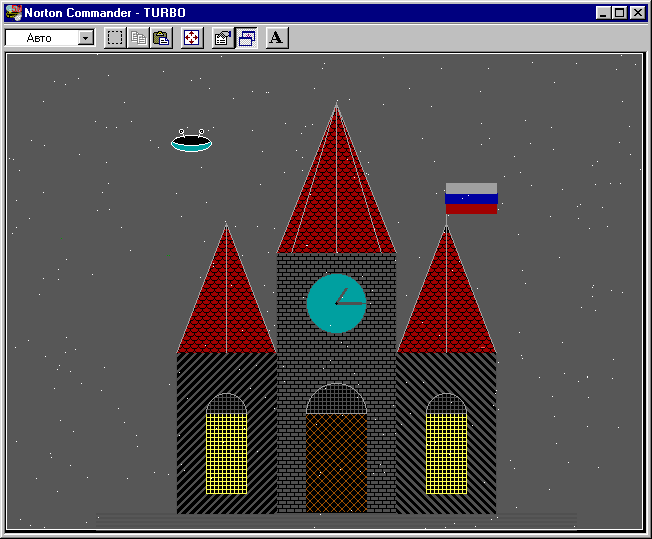
Рис. 3.21 Инопланетная тарелка

Пример 31. Демонстрационная программа "Инопланетная тарелка".

Program PR31;

Uses graph, crt;

Const r=20; pause =100; {ОДНА ДЕСЯТАЯ СЕКУНДЫ}

cher: fillpatternType=($f7,$f7,$eb,$1c,$7f,$7f,$be,$c1);

{ЧЕРЕПИЦА}

kirp: fillpatternType= ($7f,$7f,$7f,$00,$f7,$f7,$f7,$00);

{КИРПИЧ}

Var

driv, mode, error: integer;

x1, x2, y1, y2: integer;

d, m, e, xm, ym, x, y: integer;

lx, ly, rx, ry, i, dx, dy: integer;

size, width, height: integer;

saucer: pointer;

Begin

driv := detect;

InitGraph(driv, mode, 'd:\tp\bgi');

error := graphresult;

if error <> grok

then begin writeln(grapherrormsg(error)); HALT end;

SetColor(7);

line(440,130,440,170);

line(330,50,390,200); {ЦЕНТРАЛЬНАЯ КРЫША}

line(270,200,330,50);

line(270,200,390,200);

setfillpattern (cher, red);

floodfill (330,199, 7); {ЧЕРЕПИЦА НА ЦЕНТРАЛЬНОЙ КРЫШИ}

line(330,49,330,200);

line(330,50,285,200);

line(330,50,375,200);

line(390,300,440,170); {ПРАВАЯ КРЫША}

line(440,170,490,300);

line(390,300,490,300);

floodfill (440,299, 7); {ЧЕРЕПИЦА НА ПРАВОЙ КРЫШИ}

line(440,130,440,300); {ФЛАГШТОК}

line(170,300,220,170); {ЛЕВАЯ КРЫША}

line(220,170,270,300);

line(170,300,270,300);

floodfill (220,299, 7); {ЧЕРЕПИЦА НА ЛЕВОЙ КРЫШИ}

line(220,170,220,300);

setfillstyle(1,red); {ФЛАГ НА ПРАВОЙ КРЫШЕ}

bar(440,150,490,160);

setfillstyle(1,blue);

bar(439,140,491,150);

setfillstyle(1, 7);

bar(440,130,490,140);

setfillstyle(2,darkgray); {ФУНДАМЕНТ ЗАМКА}

bar(90,460,570,480);

Setcolor(8);

Rectangle(270,200,390,460);

setfillpattern (kirp, darkgray); {ЦЕНТРАЛЬНАЯ БАШНЯ}

floodfill (300,300,8);

setfillstyle(8,brown); {ДВЕРЬ}

bar(300,360,360,458);

Setcolor(8);

setfillstyle(4,darkgray); {ЛЕВАЯ БАШНЯ}

bar(170,300,270,460);

line(170,300,170,460); {ЖЕЛТОЕ ОКНО В ЛЕВОЙ БАШНЕ}

setfillstyle(7,yellow);

bar(200,360,240,440);

setfillstyle(5,darkgray); {ПРАВАЯ БАШНЯ}

bar(390,300,490,460);

line(490,300,490,460);

setfillstyle(7,yellow); {ЖЕЛТОЕ ОКНО В ПРАВОЙ БАШНЕ}

bar(420,360,460,440);

setfillstyle(1,cyan); {ЧАСЫ НА ГЛАВНОЙ БАШНЕ}

sector(330,250,0,360,30,30);

SetLineStyle(0,0,3);

line(330,250,340,235); {СТРЕЛКИ ЧАСОВ}

line(330,250,355,250);

SetLineStyle(0,0,1);

SetColor(7);

setfillstyle(7,8);

sector(330,360,0,180,30,30);

sector(440,360,0,180,20,20);

sector(220,360,0,180,20,20);

SetColor(15); {СТРОИМ ЛЕТАЮЩУЮ ТАРЕЛКУ НА ЧЕРНОМ ФОНЕ НЕБА}

x:=r*5;

y:=r*2;

xm:=getmaxx div 4;

ym:=getmaxy div 4;

ellipse(x,y,0,360,r,r div 3 + 2);

ellipse(x,y-4,190,357,r,r div 3);

line(x+7,y-6,x+10,y-12);

line(x-7,y-6,x-10,y-12);

circle(x+10,y-12,2);

circle(x-10,y-12,2);

setfillstyle(1,cyan);

floodfill(x+1,y+4,white); {КОНЕЦ ПОСТРОЕНИЯ ТАРЕЛКИ}

lx:= x-r-1; {ВЫЧИСЛЯЕМ КООРДИНАТЫ ФРАГМЕНТА, ТАРЕЛКИ}

ly:= y-14;

rx:= x+r+1;

ry:= y+r div 3+3;

width:=rx-lx+1;

height:=ry-ly+1;

size:=imagesize(lx,ly,rx,ry); {ОПРЕДЕЛЯЕМ РАЗМЕР НЕОБХОДИМЫЙ

ПАМЯТИ}

getmem(saucer, size); {ОТВОДИМ ПАМЯТЬ ДЛЯ ХРАНЕНИЯ ФРАГМЕНТА}

getimage(lx,ly,rx,ry,saucer^); {ЗАБИРАЕМ ТАРЕЛКУ В ПАМЯТЬ}

PutImage(lx,ly, saucer^, xorput); {СТИРАЕМ ТАРЕЛКУ ЕЕ

ИНВЕРСИЕЙ – XORPUT}

rectangle(0,0,4*xm,4*ym); {РИСУЕМ ПО РАЗМЕРУ ЭКРАНА РАМКУ}

xm:=4*xm; {МАКСИМАЛЬНЫЕ КООРДИНАТЫ X И Y ДЛЯ СНЕГА}

ym:=4*ym;

for i:=1 to 300 {ФОРМИРУЕМ 300 СНЕЖИНОК БЕЛОГО ЦВЕТА}

do PutPixel(random(xm),random(ym),white);

x:=xm div 2; y:=ym div 2; {ТАРЕЛКА ПОЯВЛЯЕТСЯ В ЦЕНТРЕ ЭКРАНА}

dx:=10; dy:=10; {СМЕЩЕНИЕ ТАРЕЛКИ НА 10 ПИКСЕЛЕЙ}

repeat

PutImage(x,y, saucer^,xorput);

delay(pause); {ТАРЕЛКА ЗАВИСАЕТ НА 0.1 СЕКУНДЫ}

PutImage(x, y, saucer^, xorput); {СТИРАЕМ ТАРЕЛКУ ЕЕ

ИНВЕРСИЕЙ - XORPut}

REPEAT

x:=x+dx; y:=y+dy;

if(x<0) or (x+width+1>xm) or (y<0) or (y+height+1>ym)

then begin {Тарелка касается границ экрана}

x:=x-dx; y:=y-dy; {ШАГ НАЗАД И МЕНЯЕМ СЛУЧАЙНЫМ ОБРАЗОМ

dx, dy}

dx:=getmaxx div 10 - random(getmaxx div 5);

dy:=getmaxy div 30 - random(getmaxy div 15);

end

else break

Until false;

Until keypressed;

closegraph

end.

В отличие от предыдущей программы в примере 140 фон не однородный. Поэтому вывод фрагмента на экран производится процедурой PutImage дважды с параметром XORPut. При первом выводе тарелка появляется в центре экрана и движется под углом в сорок пять градусов в правую нижнюю часть экрана. Касаясь границы экрана она случайным образом меняет направление и скорость своего движения. Каждый пиксель тарелки меняет свой цвет в соответствии с цветом фона, поэтому создается эффект цветовых переливов тарелки. Поскольку в фоне преобладают темные тона, то в целом цветовая гамма тарелки поддерживает основные цвета исходного фрагмента. После вывода тарелки - пауза в одну десятую секунды. После чего происходит восстановление фона повторным выводом фрагмента процедурой PutImage с параметром XORPut. Для инерционного человеческого взгляда такое движение тарелки кажется непрерывным.