4.2 Использование функции в циклических процессах
В этом разделе необходимо разработать формулу для функции, с помощью которой и решить поставленную задачу. Разбить алгоритм на две части - на основную программу и пользовательскую функцию. Необходимо описать алгоритмы основной программы и функции с помощью двух блок-схем. Составить циклическую программу и для введенных с клавиатуры значений параметров рассчитать требуемые величины.
Найти предел последовательности , которая вычисляется по формуле
,
.
Величину b ввести с
клавиатуры. Вычисления остановить при
выполнении условия
.
При составлении программы
реализовать в виде функции A(n).
Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении
условия
.
При составлении программы
реализовать в виде функции A(n).
Найти предел последовательности , которая вычисляется по формуле
,
.
Величину b ввести с клавиатуры. Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
Найти предел функции
,
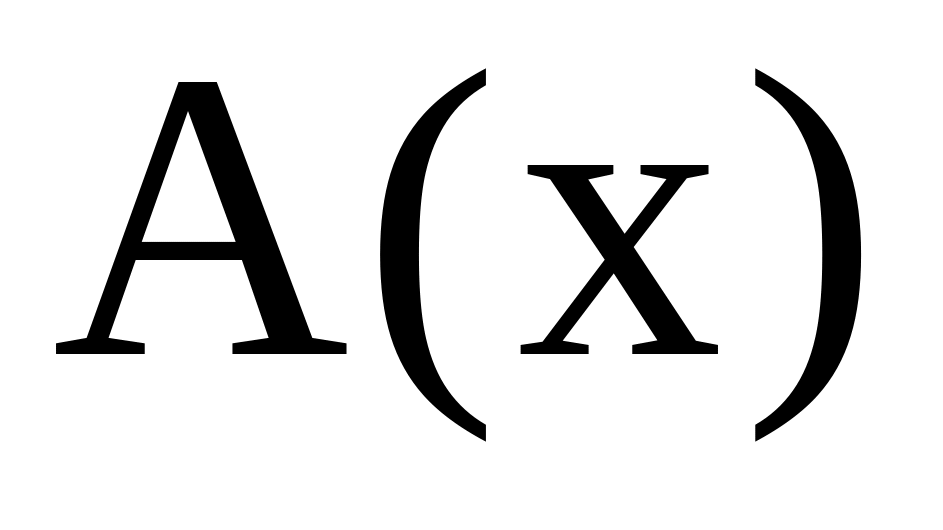которая вычисляется по формуле
.
Вычисления остановить при выполнении
условия
.
При составлении программы
реализовать в виде пользовательской
функции A(n).
Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
С клавиатуры ввести числа A, B, C и D. Для каждой тройки этих чисел, соответствующих сторонам треугольника, вычислить площадь, если такой треугольник можно построить. Для проверки чисел и вычисления площади использовать функцию вида
.
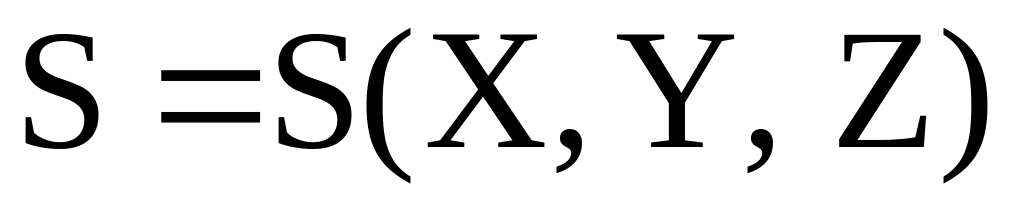Если треугольник построить нельзя, то
принять S = 0.С клавиатуры ввести числа A, B, C. Найти медианы треугольника со сторонами A, B, C, используя следующую формулу - длина медианы
,
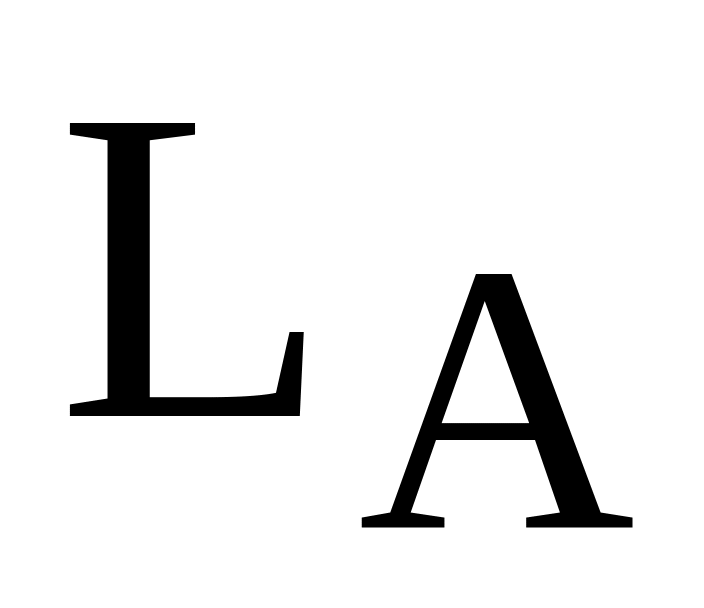проведенной к стороне A
равна
.
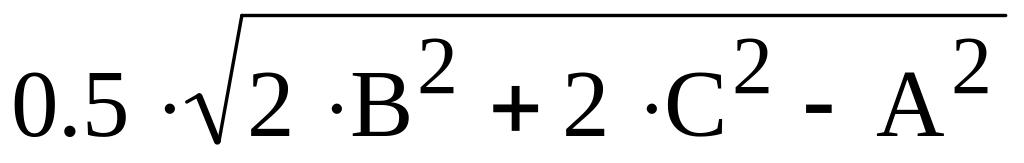Требуется найти медианы треугольника,
который можно сформировать из медиан
исходного треугольника. Для определения
длин медиан использовать функцию вида
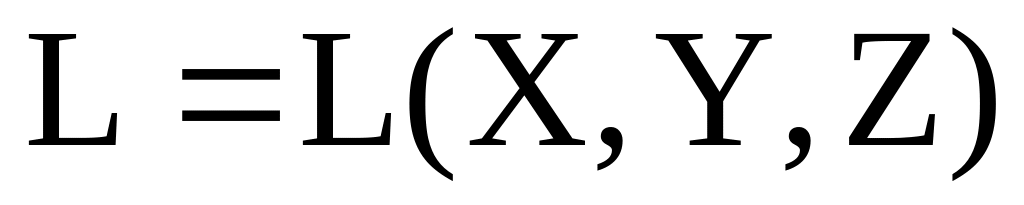.Вычислить интеграл функции
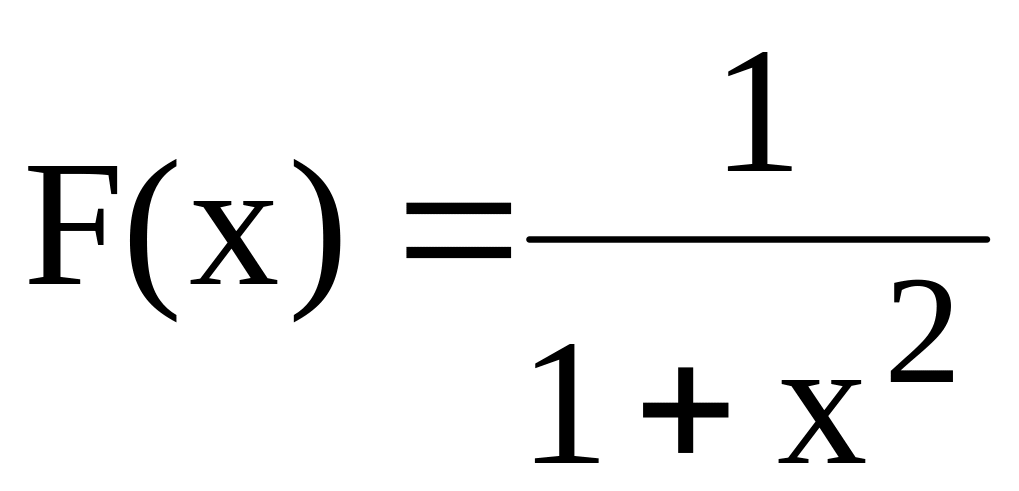по формуле Симпсона:
,
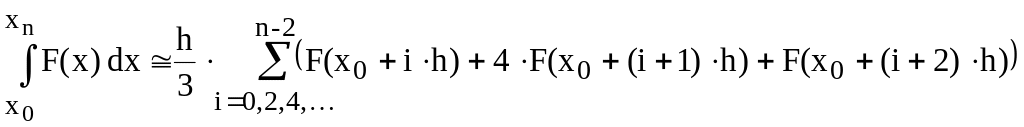где
n =100.
Вычислить интеграл функции
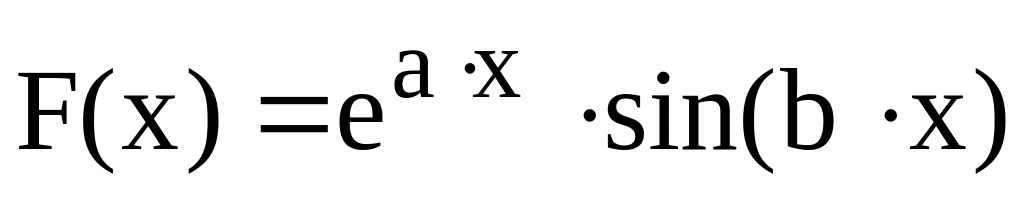по формуле трапеций:
,
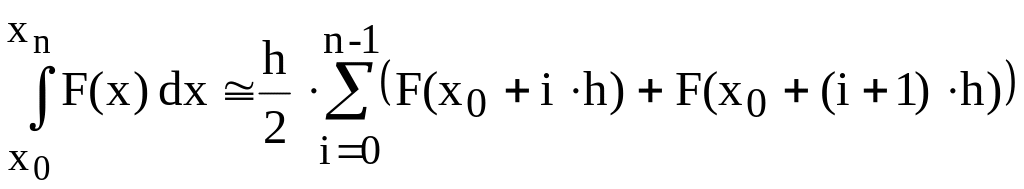где
n =1200.
Вычислить число сочетаний
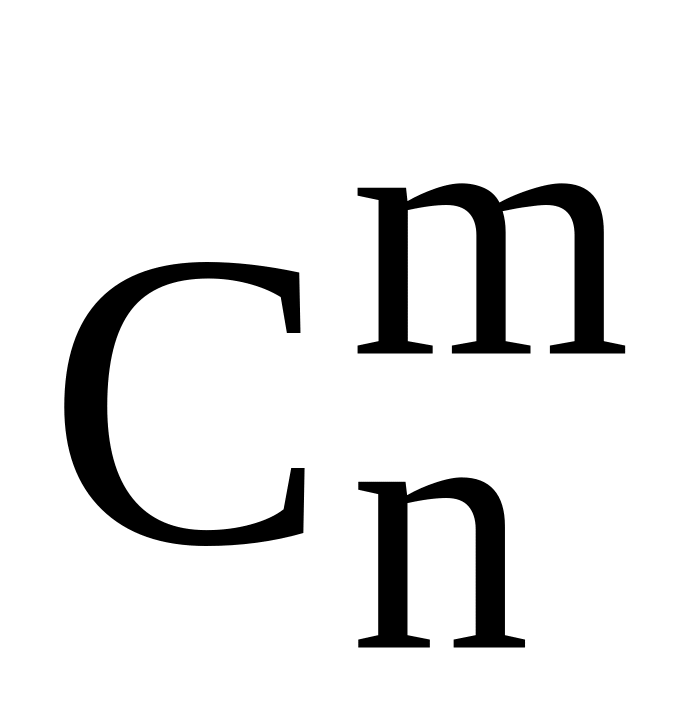из n по m,
где m и n
натуральные числа (m
n), с помощью формулы:
.
Для определения K! использовать рекурсивную функцию.
Вычислить величину Y:
,
где m и n неотрицательные целые числа (m n).
Для определения
использовать рекурсивную функцию.
Вычислить величину Y:
,
где m и n неотрицательные целые числа (m n).
Для определения
использовать рекурсивную функцию.
Вычислить величину Y для заданных с клавиатуры значений x и n:
,
n - раз
где
.
Для вычисления Y использовать
рекурсивную функцию вида
.
Последовательность чисел Фибоначчи {
}
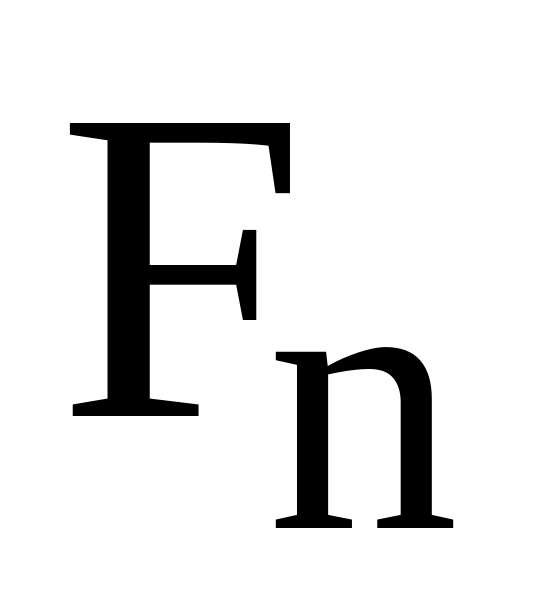определяется рекуррентным соотношением
,
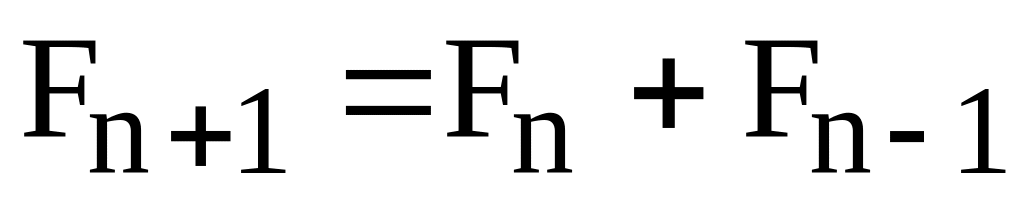причем
.
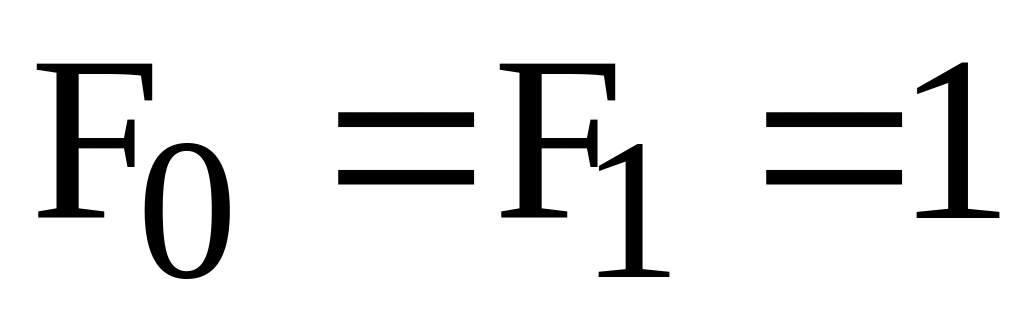По заданному с клавиатуры n,
найти значение
.
В расчетах использовать рекурсивную
функцию вида
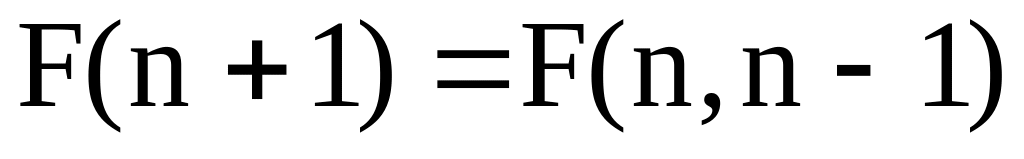.Вычислить значение полинома Чебышева
,
где n и x
вводятся с клавиатуры. В расчетах
следует использовать рекурсивную
функцию
,
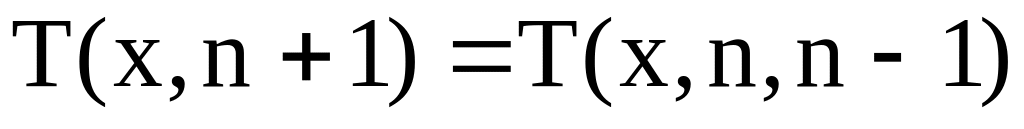соответствующую рекуррентной зависимости
,
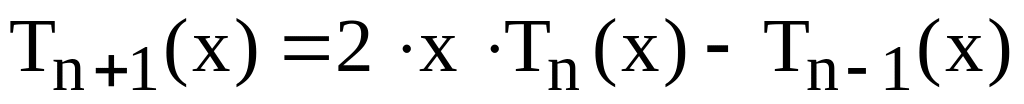причем
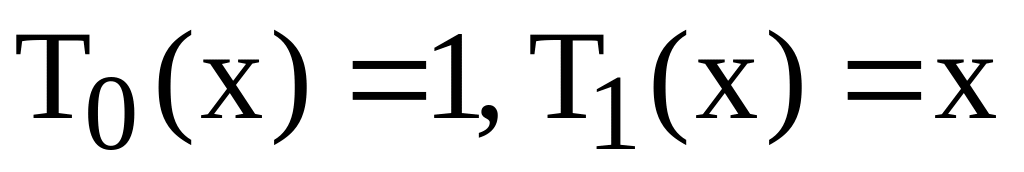.По заданным с клавиатуры параметрам a и b вычислить :
,
где
.
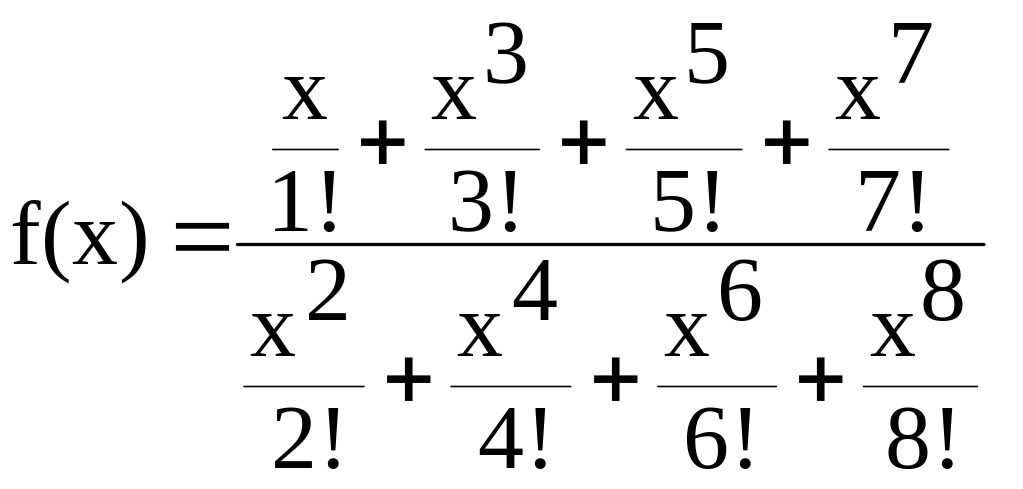Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении
условия
.
При составлении программы
реализовать в виде функции A(n).
22. Найти предел последовательности , которая вычисляется по формуле:
,
.
Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
23. Найти предел последовательности , которая вычисляется по формуле
,
.
Значение Х>1 вводится с клавиатуры. Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
24. Найти предел последовательности , которая вычисляется по формуле
,
.
Значение |Х|<1 вводится с клавиатуры. Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
25. Вычислить интеграл функции
по формуле Ньютона:
,
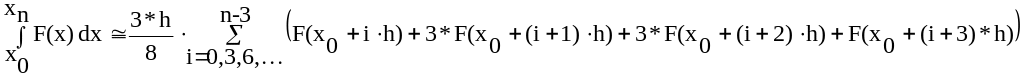где
n =200.
26. Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
27. Найти предел последовательности , которая вычисляется по формуле
,
.
Значение |b|<1 вводится с клавиатуры. Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
28. Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).
29. Найти предел последовательности , которая вычисляется по формуле
,
.
Значение Х вводится с клавиатуры
.
Вычисления остановить при выполнении
условия
.
При составлении программы
реализовать в виде функции A(n).
30. Найти предел последовательности , которая вычисляется по формуле
,
.
Вычисления остановить при выполнении условия . При составлении программы реализовать в виде функции A(n).