4. Методы наблюдения интерференции света. Метод Юнга.

6. Расчет интерференциоии от 2-х источников света

Существуют несколько методов наблюдения интерференции света. Примерами являются метод Юнга и зеркал Френеля.

Юнг получил полосы интерференции способом – пучок света от солнца падал на экран с малым отверстием или узкой щелью. Затем на экран с двумя узкими отверстиями S1 и S2. Световые пучки от S1 и S2 накладывались, в результате чего получается 2 перекрещивающихся, расходящихся когерентных пучка света. На экране в месте перекрывания пучков наблюдались параллельные интерференционные полосы.

d- расстояние между источниками, - расстояние от источников до экрана, - расстояние от точки О до рассматриваемой точки А.

Интенсивность в любой точке А определяется оптической разностью хода: , так как .

Из рисунка следует, что

, , тогда

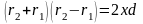
, так как , .

, , .

Найдем координаты максимумов:

, отсюда ,

координаты минимумов:

, отсюда .

Расстояние между соседними максимумами равно:

,

а между соседними минимумами:

.

Расстояние между соседним максимумом и минимумом:

5. Методы наблюдения интерференции света. Зеркала Френеля.

Существуют несколько методов наблюдения интерференции света. Примерами являются метод Юнга и зеркал Френеля.

Зеркала Френеля

Два плоских соприкасающихся зеркала ОМ и ON располагаются так, что их отражающие поверхности образуют угол, близкий к π (рис.2.5). Соответственно угол φ на рисунке очень мал.

Параллельно линии пересечения зеркал О на расстоянии r от нее помещается прямолинейный источник света S (например, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников S1 и S2.

Непрозрачный экран Э1 преграждает свету путь от источника S к экрану Э.

Луч OQ представляет собой отражение луча SO от зеркала ОМ, луч ОР — отражение луча SO от зеркала ON. Легко сообразить, что угол между лучами ОР и OQ равен 2π. Поскольку S и S1 расположены относительно ОМ симметрично, длина отрезка OS1 равна OS, т.е. r. Аналогичные рассуждения приводят к тому же результату для отрезка OS2. Таким образом, расстояние между источниками S1 и S2 равно:

Из рис.2.5 видно, что Следовательно, где b — расстояние от линии пересечения зеркал О до экрана Э.Подставив найденные нами значения d и l при рассмотрении интерференции (2.28),получим ширину интерференционной полосы:

Область перекрытия волн PQ имеет протяженность Разделив эту длину на ширину полосы Δх, найдем максимальное число интерференционных полос, которое можно наблюдать с помощью зеркал Френеля при данных параметрах схемы: