20)Электрическое смещение, его связь с поляризованностью.

Вектор электрического смещения, который для электрически изотроп­ной среды, по определению, равен

Вектор электрического смещения можно выразить как

Единица электрического смещения — кулон на метр в квадрате (Кл/м²).

Аналогично, как и поле Е, поле D изображается с помощью линий электрического смещения, направление и густота которых определяются точно так же, как и для линий напряженности (см. §79). Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь. Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверх­ность

где D_n — проекция вектора D на нормаль n к площадке dS.

В неоднородной диэлектрической среде   имеет различные значения, изменяясь на границах диэлектриков скачкообразно (претерпевая разрыв). Это затрудняет применение формул, описывающих взаимодействие зарядов в вакууме. Что касается теоремы Гаусса, то в этих условиях она вообще теряет смысл. В самом деле, благодаря различной поляризуемости разнородных диэлектриков напряженности поля в них будут различными. Поэтому различно и число силовых линий в каждом диэлектрике (рис.14.6).

Часть линий, исходящих из зарядов, окруженных замкнутой поверхностью, будет заканчиваться на границе раздела диэлектриков и не пронижет данную поверхность. Это затруднение можно устранить, введя в рассмотрение новую физическую характеристику поля – вектор электрического смещения

P – поляризованность

СИ: [D] = 1

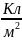
Аналагично, как и E, поле D изображается с помощью линий электрического смещения, направление и густота которых определяется точно так же, как и для линий напряжённости.

21. Теорема Гаусса для электростатического поля в диэлектрике.

22. Проводники в электростатическом поле. Электростатическая индукция.

К проводникам относят вещества, у которых имеются свободные заряженные частицы, способные двигаться упорядоченно по всему объему тела под действием электрического поля. Заряды таких частиц называют свободными. 

Проводниками являются металлы, некоторые химические соединения.

При внесении в электрическое поле тела из проводника свободные заряды в нем приходят в движение. Перераспределение зарядов вызывает изменение электрического поля. Движение зарядов прекращается только тогда, когда напряженность электрического поля в проводнике становится равной нулю.

Электростатическая индукция в проводниках

Перераспределение зарядов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды внутри тела практически полностью не скомпенсируют внешнее электрическое поле.

Электростатическая индукция в диэлектриках

Диэлектрики в электростатическом поле поляризуются.

22. Электроемкость уединенного проводника. Электроемкость конденсатора.

Величину   (1)  называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника задается зарядом, сообщение которого проводнику изменяет его потенциал на единицу. 

Электрическая емкость конденсатора. Физическая величина, определяемая отношением заряда q одной из пластин конденсатора к напряжению между обкладками конденсатора, называется электроемкостью конденсатора:

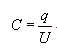
24. Соединение конденсаторов

Параллельное соединение конденсаторов. При параллельном со единении конденсаторов потенциал пластин, соединенных с положительным полюсом источника, одинаков и равен потенциалу этого полюса. Соответственно потенциал пластин, соединенных с отрицательным полюсом, равен потенциалу этого полюса. Следовательно, напряжение, приложенное к конденсаторам, одинаково. Общий заряд Qобщ=Q1+Q2+Q3. Так как Q=CU, то Qобщ=CобщU; Q1=C1U; Q2=C2U; Qз=C3U и СобщU=С1U+С2U+ C3U. Таким образом, общая, или эквивалентная, ёмкость при параллельном соединении конденсаторов равна сумме емкостей отдельных конденсаторов: Cобщ=С1+C2+С3. Следовательно, при параллельном соединении одинаковых конденсаторов емкостью C общая емкость: Cобщ=nC.

Последовательное соединение конденсаторов. При последователь ном соединении конденсаторов на пластинах будут одинаковые заряды. На внешние электроды заряды поступают от источника питания. На внутренних электродах конденсаторов С1 иС3 удерживается такой же заряд, как и на внешних. Но поскольку за ряды на внутренних электродах получены за счет раз деления зарядов с помощью электростатической индукции, заряд конденсатора С2 имеет такое же значение. Найдем общую емкость для последовательного соединения конденсаторов. Так как U=U1+U2+U3, где U=Q/Cобщ; U1=Q/C1; U2= Q/C2; U3=Q/C3, то Q/Cобщ=Q/C1+Q/C2+Q/C3. Сократив на Q, получим 1/Cобщ=1/C1+1/C2+1/Сз. При последовательном соединении двух конденса торов: Cобщ=C1C2/(C1 + C2). При последовательном соединении п одинаковых конденсаторов емкостью С каждый: Cобщ=С/n.