7. Закон Био - Савара – Лапласа, его применение для расчета индукции магнитного поля, созданного:
а) прямолинейным проводником с током конечной длины, бесконечно
длинным проводником с током;
б) в центре кругового проводника с током.
Магнитное поле постоянных токов различной формы исследовалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты их опытов были обобщены французским ученым П. Лапласом.
Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 1) индукцию поля dB, равен
где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор, который проведен из элемента dl проводника в точку А поля, r - модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с направлением касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта совпадает с направлением тока в элементе.
Модуль вектора dB задается выражением
где α — угол между векторами dl и r.
Аналогично электрическому, для магнитного поля выполняется принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
Используя данные формулы для расчет характеристик магнитного поля (В и Н) в общем случае достаточно сложен. Однако если распределение тока имеет какую-либо симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции дает возможность просто рассчитать некоторые поля. Рассмотрим два примера.
8. Закон полного тока (теорема о циркуляции вектора индукции магнитного поля), его применение для расчета индукции поля длинного соленоида.
Сформулируем теорему о циркуляции вектора магнитной индукции (закон полного тока): циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур
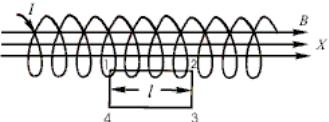
Магнитную индукцию поля бесконечно длинного соленоида можно вычислить, используя закон полного тока. Соленоид представляет собой тонкий провод, навитый плотно виток к витку на цилиндрический каркас. Он эквивалентен системе одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен относительно любой перпендикулярной его оси плоскости. В любой точке внутри и вне соленоида вектор B может иметь лишь направление параллельное оси. Возьмем прямоугольный контур (1–2–3–4). Циркуляцию B по этому контуру (1–2–3–4) можно представить следующим образом:
9. Силы в магнитном поле (сила Ампера, сила Лоренца).
Действие магнитного поля на проводник с током
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
F=B.I.ℓ. sin α — закон Ампера.
Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.
Сила,
действующая на заряженную движущуюся
частицу в магнитном поле, называется силой
Лоренца: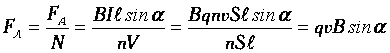 
Правило левой руки сформулировано для положительной частицы. Сила, действующая на отрицательный заряд будет направлена в противоположную сторону по сравнению с положительным.