3.Теорема об изменении количества движения точки

Выберем основной закон движения в форме (13.2.4)

Так как масса m = const, то ее можно внести под знак дифференциала и уравнение (14.2.1) переписать как

Производная от количества движения по времени равна геометрической сумме действующих на точку сил.

Если точка массы m движется под действием силы , и в момент времени t = 0 имеет скорость , а в момент времени - скорость , то:

и интегрируя получаем:

Подставляем в правую часть соотношение (14.1.4):

Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за тот же промежуток времени.

Уравнение (14.2.4) представляет собой теорему об изменении количества движения точки (рис. 73)

В проекциях на оси координат уравнение (14.2.4) запишется:

4.Теорема об изменении кинетического момента точки

Теорема:первая производная по времени от кинетического момента точки относительно какого-либо центра равна моменту силы относительно того же центра.

Доказательство: Продифференцируем момент количества движения по времени

, , следовательно , (*)

что и требовалось доказать.

5.Теорема об изменении кинетической энергии точки

Теорема. Дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.

Доказательство: Основной закон динамики .

Умножим левую и правую части уравнения скалярно на справа, получаем . - элементарная работа.

- дифференциал от кинетической энергии.

, что и требовалось доказать.

Теорема. Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке.

Теорема. Изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на этом же перемещении.

6.Центр масс механической системы

Рассмотрим механическую систему, которая состоит из конечного числа материальных точек с массами , а положение точек в пространстве задается радиус-векторами , то

Ц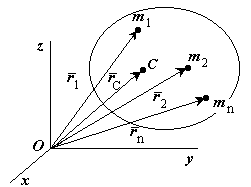 ентром масс механической системы называется геометрическая точка С, радиус-вектор которой определяется выражением

где - масса системы.

Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами . Суммы в пределе переходят в интегралы и центр масс определяется выражением

Центр масс является не материальной точкой, а геометрической. Центр масс характеризует распределение масс в системе.

Координаты центра масс имеют вид:

Для тел типа тонкого листа (поверхность) и тонкой проволоки (линия) и , где - поверхностная и линейная плотности соответственно. Интегралы вычисляются по поверхности и линии.

7.Количество движения системы

Количеством движения системы материальных точек называется векторная сумма количеств движений отдельных точек системы.

Единицей измерения количества движения в СИ является –

Количество движения системы можно выразить через массу системы и скорость центра масс.