22. Определение ускорений точек твердого тела при плоском движении

Покажем, что ускорение любой точки М плоской фигуры (так же, как и скорость) складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фигуры. Положение точки М по отношению к осям Оxy (см.рис.30) определяется радиусом-вектором где . Тогда

.

В правой части этого равенства первое слагаемое есть ускорение полюса А, а второе слагаемое определяет ускорение , которое точка м получает при вращении фигуры вокруг полюса A. следовательно,

.

Значение , как ускорения точки вращающегося твердого тела, определяется как

где и - угловая скорость и угловое ускорение фигуры, а - угол между вектором и отрезком МА (рис.41). Таким образом, ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление ускорения , находятся построением соответствующего параллелограмма (рис.23). Однако вычисление с помощью параллелограмма, изображен­ного на рис.23, усложняет расчет, так как предварительно надо бу­дет находить значение угла , а затем - угла между векторами и , Поэтому при решении задач удобнее вектор заменять его касательной и нормальной составляющими и пред­ставить в виде . При этом вектор направлен перпендикулярно АМ в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор всегда направлен от точки М к полюсу А (рис.42). Численно же

.

Если полюс А движется не прямолинейно, то его ускорение мо­жно тоже представить как сумму касательной и нормальной составляющих, тогда .

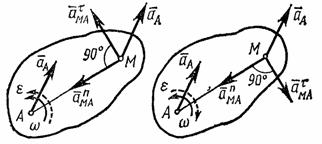
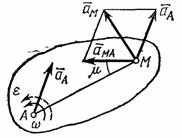
Рис.41 Рис.42 Наконец, когда точка М движется криволинейно и ее траекто­рия известна, то можно заменить суммой .

23. Сферическое движение твердого тела. Углы Эйлера. Кинематические уравнения сферического движения твердого тела.

Вращением твердого тела вокруг неподвижной точки С (сферическим движением) называют такое движение, при котором одна точка тела остаётся неподвижной во все время движения. Траектории всех точек тела при таком движении располагаются на поверхностях сфер, описанных из неподвижной точки.

Учитывая, что свободное твердое тело имеет шесть степеней свобо­ды и закрепление одной точки тела уменьшает число степеней свободы на три единицы, получим, что при сферическом движении тело имеет три степени свободы. Три независимых параметра, определяющих положение тела, можно задать различными способами.

Рассмотрим обобщенные координаты, введенные Эйлером и называемые уг­лами Эйлера. Эти углы обладают тем свойством, что через них легко выражаются координаты любой точки тела.

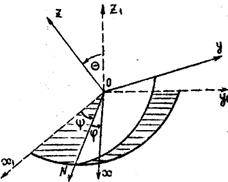
Через неподвижную точку О твердо­го тела проведем неподвижную систему координат Оx₁y₁z_1, относительно которой будем рас­сматривать движение тела (риc.7).

Рис.7

 Другую систему координат Оxyz скрепим с самим телом, вращающимся вокруг неподвижной точки 0. Положение тела определится положением под­вижной системы координат относительно неподвижной. Пусть ON - линия узлов - прямая пересечения плоскостей x₁y₁z₁ и xyz.

За положительное направление на линии узлов выбираем то её нап­равление, с которого поворот от оси Оz₁ к оси Оz на наименьший угол виден происходящим против часовой стрелки.

Угол прецессии определяет положение линии узлов относительно неподвижной координатной оси Ох_1. Для изменения этого угла тело должно вращаться вокруг неподвижной координатной оси Оz₁, которую называют осью прецессии. Угол считается положительным, если он отсчитывается против часовой стрелки, если смотреть с положительного направлении оси Оz₁ (от оси Ох₁ к оси ОN). Угол между линией ОN и осью Ох назы­вается углом собственного вращения. Для изменения угла тело должно вращаться вокруг оси Z, называемой осью собственного вращения. Угол считается положительным, если он отсчитывается против хода часовой стрелки, если смотреть с положительного конца оси Oz.

Угол между плоскостями xOy и x₁Oy₁ лежит в плоскости zOz_1. Он называется углом нутации. Для изменения угла тело должно вращаться вокруг линии узлов. Угол будет считаться положительным, если он отсчитывается от оси Oz₁ к оси Oz против хода часовой стрелки, если смотреть с положительного направления линии узлов.

При вращении тела вокруг неподвижной точки изменяются все три угла Эйлера. При этом тело можно перевести из одного положения в другое, изменяя углы Эйлера не все сразу, а последовательно, в любом порядке, начиная с любого угла.

Это позволяет утверждать, что углы Эйлера являются независимыми пара­метрами. Чтобы задать уравнения сферического движения, нужно представить углы Эйлера как непрерывные, однозначные функции времени

(18)

Уравнения (18) являются кинематическими уравнениями вращения тела вокруг неподвижной точки.