
- •Аксиомы статики
- •Алгебраический и векторный моменты силы относительно точки. Момент силы относительно оси
- •Связь между векторным моментом силы относительно точки, расположенной на оси и моментом силы относительно этой оси.
- •5.Сложение сил. Сложение пар сил.
- •6. Приведение силы к заданному центру
- •7. Приведение системы сил к простейшему виду. Главный вектор и главный момент системы сил.
- •8. Частные случаи приведения системы сил к простейшему виду
- •9. Уравнения равновесия пространственной системы сил
- •10. Уравнения равновесия системы параллельных сил
- •11. Уравнения равновесия плоской системы сил.
- •12. Уравнения равновесия сходящейся системы сил.
- •13. Центр системы параллельных сил.
- •14. Центр тяжести твердого тела.
- •16.Способ задания движения точки. Определение скорости и ускорения точки.
- •18.Простейшие движения твердого тела. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях твердого тела.
- •19. Векторные выражения для определения скоростей точек твердого тела при в ращательном движении.
- •20. Плоское движение твердого тела. Разложение плоского движения твердого тела на два простейших движения.
- •21. Определение скоростей точек твердого тела при плоском движении
- •22. Определение ускорений точек твердого тела при плоском движении
- •23. Сферическое движение твердого тела. Углы Эйлера. Кинематические уравнения сферического движения твердого тела.
- •24. Мгновенная ось вращения при сферическом движении твердого тела. Определение угловой скорости и углового ускорения тела при сферическом движении.
- •25. Определение скоростей и ускорений точек твердого тела при сферическом движении.
- •27. Сложное движение точки. Определение абсолютной скорости и абсолютного ускорения точки при сложном движении.
- •28. Дифференциальные уравнения движения материальной точки. Прямая и обратная задача динамики точки.
- •29. Количество движения точки. Кинетический момент точки относительно заданного центра. Кинетическая энергия точки.
- •30. Элементарный и полный импульс силы. Элементарная и полная работа силы.
18.Простейшие движения твердого тела. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях твердого тела.
Поступательное
движение.
Поступательным называется такое движение
твердого тела, при котором любая прямая,
соединяющая две точки тела, дви-жется
параллельно самой себе. Траектории
точек твердого тела могут быть лю-быми
кривыми линиями.
Теорема:
При поступательном движении твердого
тела все точки дви-жутся поступательно,
описывают одинаковые траектории
(совпадающие при наложении) и в каждый
момент времени имеют равные скорости
и ускорения.
Докажем эту теорему.
Пусть твердое тело совершает поступательное
движение относительно системы отсчета
OXYZ. Положение точек А и В опре-делено
радиусами-векторами
![]() и
и
![]() соответственно,
а положение точки В относительно точки
А - радиусом-вектором
соответственно,
а положение точки В относительно точки
А - радиусом-вектором
![]() .
Тогда
.
Тогда
![]() ,
где
=
const, учитывая, что
,
где
=
const, учитывая, что
![]() и
и
![]() тогда
тогда
![]() ,
но
,
но
![]()
Следовательно
|![]() |=|
|=|![]() |
(1.62)
|
(1.62)
Взяв
производные от скоростей обеих точек,
![]() или
|
или
|![]() |=|
|=|![]() |
|

 Вращательным
называется движение твердого тела, при
котором все точки некоторой прямой,
связанной с телом, остаются неподвижными
во время движения. Эта прямая называется
осью вращения.
Вращательным
называется движение твердого тела, при
котором все точки некоторой прямой,
связанной с телом, остаются неподвижными
во время движения. Эта прямая называется
осью вращения.
(рис. 2.2.1)
Положение
тела определено, если задан угол
![]() между
плоскостями
между
плоскостями
![]() и
и
![]() ,
проходящими через ось вращения (
,
проходящими через ось вращения (![]() с
единичным направляющим вектором
с
единичным направляющим вектором
![]() )
(рис.
2.2.1)
. Плоскость
)
(рис.
2.2.1)
. Плоскость
![]() неподвижна,
а плоскость
неподвижна,
а плоскость
![]() жестко
связана с телом. Угол
жестко
связана с телом. Угол
![]() измеряется
в радианах и изменяется с течением
времени,
измеряется
в радианах и изменяется с течением
времени,
![]() –
уравнение вращательного движения
твердого тела. Угловая скорость
–
уравнение вращательного движения
твердого тела. Угловая скорость
![]() характеризует
изменение угла поворота с течением
времени.
характеризует
изменение угла поворота с течением
времени.
Угловое
ускорение
![]() –
характеризует быстроту изменения
угловой скорости.
–
характеризует быстроту изменения
угловой скорости.
Если
угловая скорость
![]() постоянна,
то вращение называется равномерным и
происходит по закону
постоянна,
то вращение называется равномерным и
происходит по закону
![]() .
Если угловое ускорение
.
Если угловое ускорение
![]() постоянно,
то вращение называется равнопеременным
и происходит согласно уравнениям:
постоянно,
то вращение называется равнопеременным
и происходит согласно уравнениям:
![]() ,
,
![]() .
.
Модули
скорости, ускорения, касательного,
нормального ускорений точки вращающегося
тела, находящейся на расстоянии
![]() от
оси вращения, определяются по формулам:
от
оси вращения, определяются по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Ускорение
точки составляет угол
![]() с
направлением нормали, при этом
с
направлением нормали, при этом
 .
.
19. Векторные выражения для определения скоростей точек твердого тела при в ращательном движении.
Проведем
из произвольной точки
на оси вращения радиус-вектор
![]() в рассматриваемую точку
в рассматриваемую точку
![]() тела (рис. 2.13). Тогда
тела (рис. 2.13). Тогда![]() ,
поэтому
,
поэтому
![]() ,
где
символом
,
где
символом
![]() обозначено векторное произведение
вектора угловой скорости
обозначено векторное произведение
вектора угловой скорости
![]() и радиуса-вектора
.
Вектор
перпендикулярен к плоскости, проходящей
через точку
и ось вращения, и направлен в сторону
вращения тела. Поэтому он совпадает с
вектором скорости
и радиуса-вектора
.
Вектор
перпендикулярен к плоскости, проходящей
через точку
и ось вращения, и направлен в сторону
вращения тела. Поэтому он совпадает с
вектором скорости
![]() как по величине, так и по направлению.
Таким образом,
как по величине, так и по направлению.
Таким образом,
![]() .
(2.40) А так как
.
(2.40) А так как![]() , то
, то
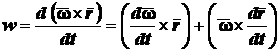 или
или
![]() .
(2.41)
.
(2.41)
Легко
показать, что вектор
![]() направлен по касательной к траектории
точки в одну сторону со скоростью, если
вращение ускоренное, и в противоположную
сторону, если оно замедленное, а вектор
направлен по касательной к траектории
точки в одну сторону со скоростью, если
вращение ускоренное, и в противоположную
сторону, если оно замедленное, а вектор
![]() направлен по радиусу к оси вращения.
Поэтому первый из них есть вектор
вращательного, а второй - центростремительного
ускорения точки:
направлен по радиусу к оси вращения.
Поэтому первый из них есть вектор
вращательного, а второй - центростремительного
ускорения точки:
![]() ;
(2.42)
;
(2.42)
![]() .
(2.43)
.
(2.43)
