
- •Аксиомы статики
- •Алгебраический и векторный моменты силы относительно точки. Момент силы относительно оси
- •Связь между векторным моментом силы относительно точки, расположенной на оси и моментом силы относительно этой оси.
- •5.Сложение сил. Сложение пар сил.
- •6. Приведение силы к заданному центру
- •7. Приведение системы сил к простейшему виду. Главный вектор и главный момент системы сил.
- •8. Частные случаи приведения системы сил к простейшему виду
- •9. Уравнения равновесия пространственной системы сил
- •10. Уравнения равновесия системы параллельных сил
- •11. Уравнения равновесия плоской системы сил.
- •12. Уравнения равновесия сходящейся системы сил.
- •13. Центр системы параллельных сил.
- •14. Центр тяжести твердого тела.
- •16.Способ задания движения точки. Определение скорости и ускорения точки.
- •18.Простейшие движения твердого тела. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях твердого тела.
- •19. Векторные выражения для определения скоростей точек твердого тела при в ращательном движении.
- •20. Плоское движение твердого тела. Разложение плоского движения твердого тела на два простейших движения.
- •21. Определение скоростей точек твердого тела при плоском движении
- •22. Определение ускорений точек твердого тела при плоском движении
- •23. Сферическое движение твердого тела. Углы Эйлера. Кинематические уравнения сферического движения твердого тела.
- •24. Мгновенная ось вращения при сферическом движении твердого тела. Определение угловой скорости и углового ускорения тела при сферическом движении.
- •25. Определение скоростей и ускорений точек твердого тела при сферическом движении.
- •27. Сложное движение точки. Определение абсолютной скорости и абсолютного ускорения точки при сложном движении.
- •28. Дифференциальные уравнения движения материальной точки. Прямая и обратная задача динамики точки.
- •29. Количество движения точки. Кинетический момент точки относительно заданного центра. Кинетическая энергия точки.
- •30. Элементарный и полный импульс силы. Элементарная и полная работа силы.
16.Способ задания движения точки. Определение скорости и ускорения точки.
Для задания движения точки можно применять один из следующих трех способов:
1) векторный, 2) координатный, 3) естественный.
1. Векторный способ задания движения точки.
П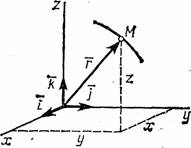 усть
точка М
движется по отношению к некоторой
системе отсчета Oxyz.
Положение этой точки в любой момент
времени можно определить, задав ее
радиус-вектор
усть
точка М
движется по отношению к некоторой
системе отсчета Oxyz.
Положение этой точки в любой момент
времени можно определить, задав ее
радиус-вектор
![]() ,
проведенный из начала координат О
в точку М
(рис. 1).
,
проведенный из начала координат О
в точку М
(рис. 1).
При движении точки
М
вектор
будет с течением времени изменяться
и по модулю, и по направлению. Следовательно,
является переменным вектором
(вектором-функцией), зависящим от
аргумента
![]() :
:
![]() .
.
Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки. Геометрическое место концов вектора определяет траекторию движущейся точки.
2. Координатный способ задания движения точки.
Положение точки можно непосредственно определять ее декартовыми координатами х, у, z (рис.1), которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости
![]() ,
,
![]() ,
,
![]() .Уравнения
представляют собой уравнения движения
точки в прямоугольных декартовых
координатах. Они определяют закон
движения точки при координатном способе
задания движения.
Чтобы получить
уравнение траектории надо из уравнений
движения исключить параметр
.Уравнения
представляют собой уравнения движения
точки в прямоугольных декартовых
координатах. Они определяют закон
движения точки при координатном способе
задания движения.
Чтобы получить
уравнение траектории надо из уравнений
движения исключить параметр
![]() .
Нетрудно
установить зависимость между векторным
и координатным способами задания
движения.
.
Нетрудно
установить зависимость между векторным
и координатным способами задания
движения.
Разложим вектор на составляющие по осям координат:
![]()
где
![]() -
проекции вектора на оси;
-
проекции вектора на оси;
![]() –
единичные векторы направленные по осям,
орты осей.
–
единичные векторы направленные по осям,
орты осей.
Так как начало вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому
![]()
3. Естественный способ задания движения точки.
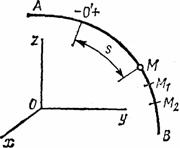
Рис.3
Естественным способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.3) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси).
Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой s, которая равна расстоянию от точки О' до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M1, М2,... . следовательно, расстояние s будет с течением времени изменяться.
Чтобы знать положение
точки М на
траектории в любой момент времени, надо
знать зависимость
![]() .
Уравнение
выражает закон движения точки М
вдоль траектории.
.
Уравнение
выражает закон движения точки М
вдоль траектории.
Вектор
скорости материальной
точки
в каждый момент времени определяется
производной по времени радиус-вектора
![]() этой
точки:
этой
точки:
![]()
Здесь
![]() —
модуль
скорости,
—
модуль
скорости,
![]() —
направленный вдоль скорости единичный
вектор касательной к траектории
в точке
.
—
направленный вдоль скорости единичный
вектор касательной к траектории
в точке
.
Скорость направлена вдоль касательной к траектории и равна по модулю производной дуговой координаты по времени.
Ускоре́ние (обычно обозначается
![]() ,
в теоретической
механике
,
в теоретической
механике
![]() ) —
производная скорости
по времени, векторная
величина, показывающая, на сколько
изменяется вектор скорости
точки (тела) при её (его) движении за
единицу времени (то есть ускорение
учитывает не только изменение величины
скорости, но и её направления). Вектор
ускорения материальной
точки
в любой момент времени находится путём
дифференцирования вектора скорости
материальной точки по времени:
) —
производная скорости
по времени, векторная
величина, показывающая, на сколько
изменяется вектор скорости
точки (тела) при её (его) движении за
единицу времени (то есть ускорение
учитывает не только изменение величины
скорости, но и её направления). Вектор
ускорения материальной
точки
в любой момент времени находится путём
дифференцирования вектора скорости
материальной точки по времени:
![]()
