9. Уравнения равновесия пространственной системы сил

1. В случае произвольной пространственной системы сил из векторных условий Вытекают 6 скалярных условий: 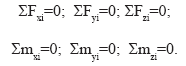2. Произвольная плоская система сил (все силы системы лежат в плоскости xy).

В этом случае лежит плоскости xy, а параллельно оси z. Тогда в скалярном виде уравнения равновесия примут вид: 3. Система сходящихся сил. Линии действия всех сил пересекаются одной точке. Если в качестве центра приведения выбрана точка пересечения линий действия сил системы, то и остается три условия равновесия: В случае системы сходящихся сил на плоскости остается 2 скалярных уравнения равновесия:

10. Уравнения равновесия системы параллельных сил

 При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

                                                       

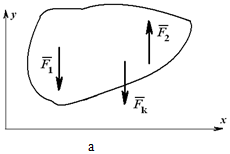
∑x_i =0;

∑M_o=0. (1.24)

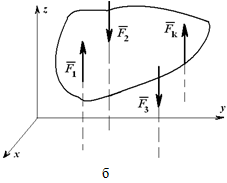
Рисунок 1.26

    Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

∑z_i =0;

∑M_ix=0; (1.25)

 ∑M_iy=0.

В частном случае линии действия сил, образующих пространственную систему, могут оказаться параллельными. Тогда одну из осей (например, ось z) выгодно расположить параллельно силам (рис. 160), а две другие оси расположатся в плоскости, перпендикулярной к линиям действия сил.

Легко понять, что для уравновешенной пространственной системы параллельных сил вместо шести уравнений можно составить лишь три: алгебраическую сумму проекций сил на ось, параллельную данным силам, и два уравнения моментов относительно двух других осей. Остальные уравнения превратятся в тождество вида 0=0.

В соответствии с расположением осей (см. рис. 160) уравнения равновесия имеют вид: ∑ Z_i = 0; (2) ∑ M_x(P_i) = 0; ∑ M_y(P_i) = 0.

Д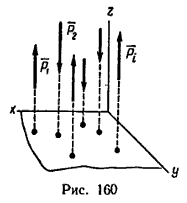 ля пространственной системы параллельных сил можно составить лишь три уравнения равновесия, поэтому, чтобы задача была статически определимой, в ней должно содержаться не более трех неизвестных сил.

11. Уравнения равновесия плоской системы сил.

Как известно, необходимыми и достаточными условиями рав­новесия пло­ской произвольной системы сил являются равенства нулю ее главного вектора и главного момента.

Существуют три формы уравнений равновесия плоской систе­мы сил. Пер­вую форму получим, спроектировав на оси координат векторное равенство и присоединив к полу­чившимся двум уравнениям равенство , выражающее условие равенства нулю главного момента: 

, , . (1.6)

Первые два уравнения называются уравнениями проекций сил на оси координат, третье - уравнением моментов. Точка может быть выбрана произ­вольно.

Легко доказать, что необходимые и достаточные условия равновесия пло­ской системы сил могут быть записаны еще в двух формах.

Вторая форма:

, , , (1.7)

где ось проекций должна быть не перпендикулярна к отрезку .

Третья форма:

, , , (1.8)

где точки не должны лежать на одной прямой.

Отметим, что для любой из трех форм уравнений равновесия число независимых между собой уравнений равновесия равно трем. Задачи, в которых все неизвестные могут быть опреде­лены из уравнений равновесия твердого тела, называются статически оп­реде­ленными. Если же неизвестных больше, чем этих уравнений, то задача оказы­вается статически неопределенной.