
- •Аксиомы статики
- •Алгебраический и векторный моменты силы относительно точки. Момент силы относительно оси
- •Связь между векторным моментом силы относительно точки, расположенной на оси и моментом силы относительно этой оси.
- •5.Сложение сил. Сложение пар сил.
- •6. Приведение силы к заданному центру
- •7. Приведение системы сил к простейшему виду. Главный вектор и главный момент системы сил.
- •8. Частные случаи приведения системы сил к простейшему виду
- •9. Уравнения равновесия пространственной системы сил
- •10. Уравнения равновесия системы параллельных сил
- •11. Уравнения равновесия плоской системы сил.
- •12. Уравнения равновесия сходящейся системы сил.
- •13. Центр системы параллельных сил.
- •14. Центр тяжести твердого тела.
- •16.Способ задания движения точки. Определение скорости и ускорения точки.
- •18.Простейшие движения твердого тела. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях твердого тела.
- •19. Векторные выражения для определения скоростей точек твердого тела при в ращательном движении.
- •20. Плоское движение твердого тела. Разложение плоского движения твердого тела на два простейших движения.
- •21. Определение скоростей точек твердого тела при плоском движении
- •22. Определение ускорений точек твердого тела при плоском движении
- •23. Сферическое движение твердого тела. Углы Эйлера. Кинематические уравнения сферического движения твердого тела.
- •24. Мгновенная ось вращения при сферическом движении твердого тела. Определение угловой скорости и углового ускорения тела при сферическом движении.
- •25. Определение скоростей и ускорений точек твердого тела при сферическом движении.
- •27. Сложное движение точки. Определение абсолютной скорости и абсолютного ускорения точки при сложном движении.
- •28. Дифференциальные уравнения движения материальной точки. Прямая и обратная задача динамики точки.
- •29. Количество движения точки. Кинетический момент точки относительно заданного центра. Кинетическая энергия точки.
- •30. Элементарный и полный импульс силы. Элементарная и полная работа силы.
5.Сложение сил. Сложение пар сил.
Сложение двух сил, приложенных в одной точке. Равнодействующая двух сил P1 и P2, направленных под углом Υ (фиг.17), по величине и направлению равна диагонали параллелограмма, построенного на этих силах (правило параллелограмма сил).
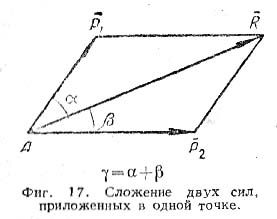
Следовательно,
R=√(P12+P22+2P1P2cosγ); P1/sinβ=P2/sinα=R/sinγ
Частные случаи:
1) γ=90°; R=√(P12+P22); cosα=P1/R; cosβ=P2/R;
2) γ=0; R=P1+P2; α=0; β=0,
т.е. равнодействующая двух сил, действующих по одной прямой в одну сторону, пампа их гумме и направлена в туже сторону;
3) γ=180°; R=P1-P2; α=0; β=180°,
т.е. равнодействующая двух сил, действующих по одной прямой в противоположные стороны, равна их разности и направлена в сторону большей силы.
Сложение двух параллельных сил. Равнодействующая двух параллельных сил Р1 и Р2 (фиг.19, а и б), направленных в одну или в противоположные стороны, равна их алгебраической сумме
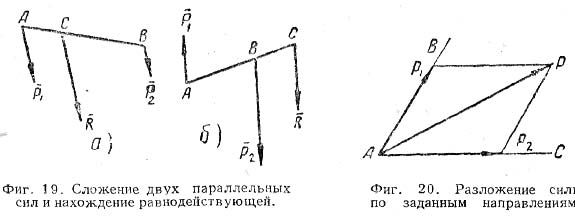
R= Р1 ± Р2 и делит отрезок между точками приложения сил, внутренним или внешним образом, на части, обратно пропорциональные этим силам:
AC/P2=BC/P1=AB/R
Это правило неприменимо для равных по величине и противоположных по направлению сил.
6. Приведение силы к заданному центру
теорема о параллельном переносе силы.
не изменяя действия силы на твердое тело, силу можно перенести
параллельно самой себе в любую точку тела - центр приведения, приложив при этом к телу пару сил с моментом, равным
моменту переносимой силы относительно центра приведения.
 Доказывается
эта вспомогательная теорема элегантно
и просто с помощью одной из аксиом
статики, позволяющей преобразовывать
системы сил в эквивалентные системы
- аксиомы о том, что к СС можно добавить
любую уравновешенную СС.
Доказывается
эта вспомогательная теорема элегантно
и просто с помощью одной из аксиом
статики, позволяющей преобразовывать
системы сил в эквивалентные системы
- аксиомы о том, что к СС можно добавить
любую уравновешенную СС.
7. Приведение системы сил к простейшему виду. Главный вектор и главный момент системы сил.
 Система
состоит из сил
Система
состоит из сил
![]() ,
приложенных в точках
,
приложенных в точках
![]() .
Выберем точку О, дальнейшем будем
называть ее центром приведения системы
сил, и перенесем последовательно эту
точку все силы системы, добавляя всякий
раз пару c моментом, равным моменту
исходной силы относительно новой точки
приложения силы. После переноса силы
обозначение добавляем «'», чтобы отличать
исходную силу от той же силы новом
положении, пару силы
.
Выберем точку О, дальнейшем будем
называть ее центром приведения системы
сил, и перенесем последовательно эту
точку все силы системы, добавляя всякий
раз пару c моментом, равным моменту
исходной силы относительно новой точки
приложения силы. После переноса силы
обозначение добавляем «'», чтобы отличать
исходную силу от той же силы новом
положении, пару силы
![]() обозначаем
обозначаем
![]() .
Силы, приложенные точке О, можно сложить
получим силу
.
Силы, приложенные точке О, можно сложить
получим силу
![]() Вектор-моменты
пар тоже можно сложить получим одну
пару, равную сумме моментов всех исходных
сил относительно центра О.
Вектор-моменты
пар тоже можно сложить получим одну
пару, равную сумме моментов всех исходных
сил относительно центра О.
![]()
Здесь
введены обозначения:
![]() –
главный вектор системы сил;
–
главный вектор системы сил;
![]() –
главный момент системы сил относительно
центра О.
Очевидно что главный вектор
системы сил не зависит от положения
центра приведения, главный момент
системы очевидно меняется при изменении
центра приведения. Заметим, что проекция
главного момента
на направление
главного вектора системы тоже не зависит
от положения центра приведения, но
доказывать это не будем.
–
главный момент системы сил относительно
центра О.
Очевидно что главный вектор
системы сил не зависит от положения
центра приведения, главный момент
системы очевидно меняется при изменении
центра приведения. Заметим, что проекция
главного момента
на направление
главного вектора системы тоже не зависит
от положения центра приведения, но
доказывать это не будем.
8. Частные случаи приведения системы сил к простейшему виду
1.
![]() –
система уравновешена.
2.
–
система уравновешена.
2.
![]() –
система приводится к равнодействующей.
3.
–
система приводится к равнодействующей.
3.
![]() –
система приводится паре сил.
4.
–
система приводится паре сил.
4.
![]() –
здесь возможно несколько подслучаев.
a)
–
здесь возможно несколько подслучаев.
a)
![]() –
сила и пара направлены вдоль одной
прямой, в этом случае говорят, что система
сводится к динаме.
b)
–
сила и пара направлены вдоль одной
прямой, в этом случае говорят, что система
сводится к динаме.
b)
![]() –
система приводится равнодействующей,
но линия действия равнодействующей не
проходит через центр приведения.
Д
–
система приводится равнодействующей,
но линия действия равнодействующей не
проходит через центр приведения.
Д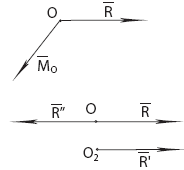 окажем
это.
Пара и сила перпендикулярны.
Силы, составляющие пару, можно расположить
так, как это показано на чертеже –
окажем
это.
Пара и сила перпендикулярны.
Силы, составляющие пару, можно расположить
так, как это показано на чертеже –
![]() и
и
![]() силы,
составляющие пару. Модули всех трех сил
можно сделать равными. Можно
изменять
направление сил, составляющих
пару, их модули, расстояние между линиями
действия так, чтобы не изменялся момент
пары.
силы,
составляющие пару. Модули всех трех сил
можно сделать равными. Можно
изменять
направление сил, составляющих
пару, их модули, расстояние между линиями
действия так, чтобы не изменялся момент
пары.
![]()
c)
![]() –
в этом случае система сил приводится
динаме, но ось динамы не проходит через
точку приведения.
В этом случае мы
можем представить вектор
–
в этом случае система сил приводится
динаме, но ось динамы не проходит через
точку приведения.
В этом случае мы
можем представить вектор![]() виде суммы двух векторов, – одного
перпендикулярного к
виде суммы двух векторов, – одного
перпендикулярного к
![]() ,
и другого, параллельного
.
Пара, перпендикулярная
,
и сила
приводятся
одной силе (см. случай b), линия действия
которой не проходит
через точку О. В
дополнение этой силе остается пара, ей
параллельная вместе они образуют динаму.
,
и другого, параллельного
.
Пара, перпендикулярная
,
и сила
приводятся
одной силе (см. случай b), линия действия
которой не проходит
через точку О. В
дополнение этой силе остается пара, ей
параллельная вместе они образуют динаму.
