27. Сложное движение точки. Определение абсолютной скорости и абсолютного ускорения точки при сложном движении.

В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО).

Обычно выбирают одну из СО за базовую («абсолютную», «лабораторную», «неподвижную», "СО неподвижного наблюдателя, «первую», «нештрихованную» и т. п.), другую называют «подвижной» («СО подвижного наблюдателя», «штрихованную» «вторую» и т. п.) и вводят следующие термины:

• абсолютное движение — это движение точки/тела в базовой СО.

• относительное движение — это движение точки/тела относительно подвижной системы отсчёта.

• переносное движение — это движение подвижной системы отсчета относительно базовой системы отсчета.

^[2] Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.

С точки зрения только чистой кинематики (задачи пересчета кинематических величин — координат, скоростей, ускорений — от одной системы отсчета к другой), являющейся в сущности предметом просто математического анализа, не имеет значения, является ли какая-то из систем отсчета инерциальной или нет; это никак не сказывается на формулах преобразования кинематических величин при переходе от одной системы отсчета к другой (то есть эти формулы можно применять и для перехода от одной произвольной неинерциальной вращающейся системы отсчета к другой).

Однако для динамики инерциальные системы отсчета (или, для практики, системы отсчета, которые можно в достаточно хорошем приближении считать инерциальными) имеют выделенное значение: в них динамические уравнения имеют гораздо более простую запись и обычно (именно поэтому) формулируются изначально именно для инерциальных систем отсчета. Поэтому особенно важны случаи перехода от инерциальной системы отсчета к другой инерциальной, а также от инерциальной к неинерциальной и обратно; последнее позволяет кроме прочего получить при желании и динамические уравнения в виде, верном для неинерциальной системы отсчета, исходя из их простой (изначальной) формулировки, сделанной для инерциальных систем отсчета.

В дальнейшем изложении, по умолчанию, для тех случаев, когда это существенно, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.

Путь представлен изменением радиуса вектора, рассматриваемого в виде суммы векторов переносного и относительного движений

(1)

Скорость

Основная статья: Теорема о сложении скоростей

Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть:

или .

Ускорение

Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени. Положение материального тела в условно неподвижной и инерциальной системе задаётся здесь вектором , а в неинерциальной системе — вектором . Положение начала координат второй системы отсчета в первой системе отсчета определяется вектором . Угловая скорость вращения неинерциальной системы отсчета относительно инерциальной задаётся вектором . Линейная относительная скорость тела по отношению к неинерциальной (вращающейся) системе отсчета ( считая ее при этом неподвижной ) задаётся вектором .

Тогда ускорение в инерциальной системе отсчета будет равно сумме:

• Здесь первый член — переносное поступательное ускорение второй системы относительно первой,

• второй член — переносное вращательное ускорение второй системы, возникающее из-за неравномерности ее вращения.

• третий член представляет собой вектор, противоположно направленный осестремительной составляющей 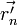вектора 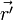, перпендикулярной (что можно получить, рассматривая это двойное векторное произведение - оно равно 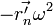) и потому представляет собой осестремительное ускорение (оно совпадает с нормальным переносным ускорением той точки вращающейся системы , с которой в данный момент совпадает движущаяся точка, не путать с нормальным ускорением движущейся точки , направленным по нормали к ее траектории ).

• сумма первых трех членов называется переносным ускорением .

• четвертый член есть Кориолисово ускорение, порождаемое взаимным влиянием переносного вращательного движения второй системы отсчета и относительного поступательного движения точки относительно ее.

• последний член 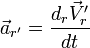   — ускорение точки относительно второй системы отсчета ( считая ее неподвижной ).