24. Мгновенная ось вращения при сферическом движении твердого тела. Определение угловой скорости и углового ускорения тела при сферическом движении.

Чтобы представить себе наглядную геометрическую картину движения тела, имеющего одну неподвижную точку, рассмотрим результат, сформулированный в теореме Даламбера – Эйлера (1749-1750 г).

В каждый момент времени движение твердого тела вокруг неподвижной точки можно рассматривать как вращение вокруг мгновенной оси, проходящей через эту точку.

мгновенная ось вращения – геометрическое ме­сто точек, скорости которых равны нулю в данный момент времени.

Ось ОР называют мгновенной осью вращения. Итак, при движении твердого тела, имеющего одну неподвижную точку, в каждый данный момент существует мгновенная ось вращения, проходящая через эту неподвижную точку.

Отсюда следует, что движение твердого тела вокруг неподвижной точки можно представить себе как непрерывный ряд последовательных вращений вокруг мгновенных осей, проходящих через неподвижную точку.

Угловая скорость , с кото­рой происходит элементарный поворот тела вокруг мгновен­ной оси вращения, называется мгновенной угловой скоростью. Условимся вектор направлять по мгновенной оси вращения в ту часть пространства, откуда вращение тела видно против хода часовой стрелки (рис.10).

При движении тела вектор в общем случае изменяется со временем и по мо­дулю, и по направле­нию, т.е. . Будем называть век­тором углового ус­корения вектор, характеризующий из­менение в данное мгновение величины и направления угловой скорости тела

. (19)

Направление вектора совпадает с направлением касательной к вектору (рис.10).

25. Определение скоростей и ускорений точек твердого тела при сферическом движении.

С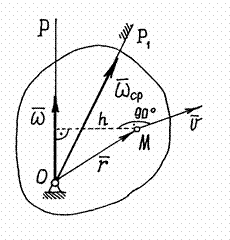 корость точек тела.По теореме Даламбера-Эйлера за малое время движение тела можно представить как вращение вокруг неподвижной оси с некоторой угловой скоростью (рис.23).

Рис.23

Тогда скорость точки : В пределе, при , угловая скорость будет приближаться к мгновенной угловой скорости , направленной по мгновенной оси вращения , а скорость точки - к истинному значению:

.

Но таким же образом находится скорость точки при вращении тела вокруг оси, по которой направлен вектор , в нашем случае – по мгновенной оси вращения . Поэтому скорость точки можно определить как скорость её при вращении тела вокруг мгновенной оси . Величина скорости (рис.23).

Ускорение точек тела. Сначала определим угловое ускорение тела . При движении тела вектор угловой скорости изменяется и по величине, и по направлению. Точка распо­ложен­ная на его конце будет двигаться по некоторой траектории со скоростью (рис.25).

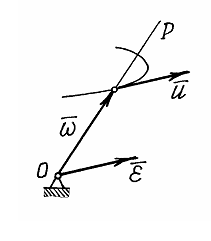Р ис.25

Если рас­сматривать вектор как ра­диус-вектор этой точки, то .

Итак. Угловое ускорение тела можно опреде­лить как скорость точки, расположенной на конце вектора угловой скорости: .

Этот результат называется теоремой Резаля.

Теперь обратимся к определению ускорения точек. Ускорение какой-либо точки тела

, есть сумма двух векторов.

Первый вектор . Модуль его , где h₁ – расстояние от точки до вектора . Направлен он перпендику­лярно и . Но таким же способом определяет­ся касательное ускорение. Поэтому первую состав­ляющую ускорения определяют как ка­сательное ускорение, предпола­гая, что тело вращается вокруг оси, совпадающей с векто­ром . И обо­значается этот вектор ускорения так

Второй вектор Модуль его , но , т.к. векторы и перпендикулярны друг другу.

Р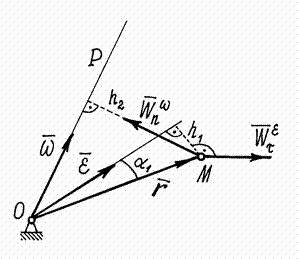 ис.26

Значит , где h₂ – расстояние от точки М до мгновенной оси , до вектора .

Направлен вектор перпендикулярно и , т.е. так же как вектор нормального ускорения при вращении вокруг оси , или вектора . Поэтому этот вектор ускорения и обозначают, соответственно, так:

Итак, ускорение точек тела, вращающегося вокруг неподвижной точки, определяется как сумма двух ускорений:

Этот результат называется теоремой Ривальса. Заметим, что в общем случае векторы и не совпадают и угол между и не равен , векторы не перпендикулярны друг другу, как это было при вращении тела вокруг неподвижной оси.