Аксиомы статики
Аксиомы статики – это законы, установленные непосредственными наблюдениями и опытной проверкой следствий, логически вытекающих из аксиом.
Аксиома 1. Система двух сил, действующих на свободное твердое тело, является уравновешенной тогда и только тогда, когда эти силы равны по модулю и действуют вдоль одной прямой в противоположные стороны.
На рис. 1.2 показаны две уравновешенные системы сил:
0;
0.
Аксиома 1 дает необходимые и достаточные условия уравновешенности системы двух сил, две следующие аксиомы устанавливают простейшие операции, приводящие к эквивалентным системам сил.
Аксиома 2. Если к данной системе сил добавить или отнять от нее уравновешенную систему сил, то полученная система сил будет эквивалентна исходной.
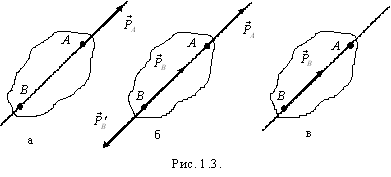
Из этой аксиомы вытекает следствие: «Действие силы на твердое тело не изменится, если перенести точку приложения силы вдоль линии ее действия».
Для
доказательства следствия рассмотрим
силу
,
приложенную в точке A
(рис.
1.3,а). В точке B на линии действия силы
приложим уравновешенную систему сил
,
где
.
Тогда в соответствии с аксиомой 2 получим
(рис.
1.3,б). Согласно аксиоме 1 система сил
0, а согласно аксиоме 2 их можно отбросить
(рис. 1.3,в),
т.е.
,
что и доказывает следствие.
Таким образом, сила, приложенная к абсолютно твердому телу, является скользящим вектором.
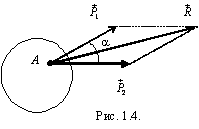
Аксиома 3 (аксиома параллелограмма сил). Система двух сил, приложенных к телу в одной точке, имеет равнодействующую, приложенную в той же точке и равную геометрической сумме сил.
Эта
аксиома не только устанавливает
существование равнодействующей
рассматриваемой системы сил
(рис.
1.4), но и дает правило ее определения:
.
Модуль равнодействующей
.
Аксиома 4 (3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
Силы взаимодействия двух тел удовлетворяют всем условиям аксиомы 1, кроме одного – они приложены к разным телам (рис. 1.5), и поэтому не образуют уравновешенную систему сил.
|
|
Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела не нарушится, если тело станет абсолютно твердым.
Другими словами, при равновесии деформируемого тела силы, действующие на него, удовлетворяют тем же условиям, что и для абсолютно твердого тела, но эти условия для деформируемого тела будут только необходимыми, не являясь достаточными.
Рассмотрим
в качестве примера деформируемого тела
нить, которая находится в равновесии
под действием двух сил
и
,
приложенных к ее концам, как показано
на рис. 1.6,а. В соответствии с аксиомой
1 эти силы должны действовать вдоль
одной прямой (вдоль нити) в противоположные
стороны и иметь одинаковые модули. Для
того, чтобы эти условия стали достаточными,
к ним следует добавить еще одно: силы,
действующие на нить, должны быть
растягивающими. При тех же условиях
абсолютно твердое тело – стержень (рис.
1.6,б) будет находиться в равновесии под
действием как растягивающих, так и
сжимающих сил.
