
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра БТС
отчет
по лабораторной работе №1
по дисциплине «Методы обработки биомедицинских сигналов и данных»
Тема: ТЕОРЕМА ОТСЧЕТОВ И ЭФФЕКТ НАЛОЖЕНИЯ
ВАРИАНТ 6
|
Студенты гр. 7501 |
|
Попадьина А.О. Исаков А.О. |
|
Преподаватель |
|
Калиниченко А.Н. |
Санкт-Петербург
2019
-
Цель работы
Получение первоначальных навыков работы с системой MATLAB; исследование теоремы отсчетов и эффекта наложения.
-
Задание на выполнение работы
-
Освоить основы работы в системе MATLAB в командном режиме и в режиме использования сценариев (М-файлов). Освоить простейшие способы расчета значений функций и их вывода в графической форме.
-
Выполнить исследование эффекта наложения на тестовых синусоидальных сигналах.
-
Выполнить исследование эффекта наложения на фрагменте ЭКГ.
-
Основные теоретические положения
Большинство реальных сигналов являются непрерывными функциями. Для обработки на компьютере требуется перевести сигналы в цифровую форму.
Д
Рисунок 1. Процесс
приведение аналогового непрерывного
сигнала в цифровую форму
Теорема Котельникова устанавливает, при каких условиях, наложенных на исходный сигнал и на частоту дискретизации можно с необходимой степенью точности восстановить исходный сигнал по его цифровым значениям.
Теорема Котельникова-Найквиста-Шеннона:
Действительный непрерывный сигнал со спектром, ограниченным в полосе частот 0 < f < fс, может быть восстановлен по его дискретным отсчетам при условии, что частота дискретизации fд > 2fс.
Наложение спектров (алиасинг)
Если попытаться оцифровать сигнал с недостаточной для него частотой дискретизации, то по полученной цифровой выборке нельзя будет верно восстановить исходный сигнал. Восстановленный сигнал будет выглядеть таким образом, как если бы частоты, лежащие выше половины частоты дискретизации, отразились от половины частоты дискретизации, перешли в нижнюю часть спектра и наложились на частоты, уже присутствующие в нижней части спектра, т.е. некоторые частотные составляющие становятся неразличимыми. Этот эффект называется наложением спектров или алиасингом.
-
Программный код
clear all;
close all;
%Задание №1
X=0:0.02:2*pi;
Y=sin(3*X);
figure('Name','Signal','NumberTitle','off');
plot(X,Y, 'm');
title ('Signal');
hold on
Y2=2*cos(5*X);
plot(X,Y2, 'c');
%Задание №2
figure('Name','Plot','NumberTitle','off');
subplot(2,1,1);
plot(X,Y, 'm');
title ('Signal');
hold on
Y2=2*cos(5*X);
subplot(2,1,2);
plot(X,Y2, 'c');
clear all;
%Задание №3
F=30;
A=10;
Fs1=500;
Fs2=100;
tmax=0.1;
tmin=0;
T1=1/Fs1;
T2=1/Fs2;
t1=tmin:T1:tmax;
t2=tmin:T2:tmax;
Y1=A*cos(2*pi*F*t1);
figure('Name','Sinusoidal signal','NumberTitle','off');
plot(t1,Y1,'r');
hold on
Y2=A*cos(2*pi*F*t2);
plot(t2,Y2,'b');
clear all;
%Задание №4
F=30;
A=10;
Fs1=500;
Fs2=100;
tmax=0.1;
tmin=0;
T1=1/Fs1;
T2=1/Fs2;
t1=tmin:T1:tmax;
t2=tmin:T2:tmax;
figure('Name','Aliasing','NumberTitle','off');
subplot(3,1,1);
Y1Fs1=A*cos(2*pi*F*t1);
Y1Fs2=A*cos(2*pi*F*t2);
plot(t1,Y1Fs1,'r');
hold on
plot(t2,Y1Fs2,'b');
subplot(3,1,2);
Y2Fs1=A*cos(2*pi*(F+Fs2)*t1);
Y2Fs2=A*cos(2*pi*(F+Fs2)*t2);
plot(t1,Y2Fs1,'r');
hold on
plot(t2,Y2Fs2,'b');
subplot(3,1,3);
Y3Fs1=A*cos(2*pi*(Fs2-F)*t1);
Y3Fs2=A*cos(2*pi*(Fs2-F)*t2);
plot(t1,Y3Fs1,'r');
hold on
plot(t2,Y3Fs2,'b');
clear all;
%Задание №5
Fs=1200;
T=1/Fs;
Y=load('R1_06.txt');
LY=length(Y);
tmin=0;
tmax=LY*T;
K1=2; %коэффициент прореживания
F1s=Fs/K1;
T1=1/F1s;
t1=tmin:T1:tmax-T1;
LY1=LY/K1;
for i=1:LY1
Y1(i)=Y((i-1)*K1+1);
end;
K2=25;
F2s=Fs/K2;
T2=1/F2s;
t2=tmin:T2:tmax-T2;
LY2=LY/K2;
for i=1:LY2
Y2(i)=Y((i-1)*K2+1);
end;
figure('Name','ECG Without decimation/decimation','NumberTitle','off');
subplot(3,1,1);
t=tmin:T:tmax-T;
Yist=transpose(Y);
plot(t,Yist);
set(gca,'Ylim',[-1000 2000]);
subplot(3,1,2);
plot (t1,Y1);
set(gca,'Ylim',[-1000 2000]);
subplot(3,1,3);
plot (t2,Y2);
set(gca,'Ylim',[-1000 2000]);
-
Графики, полученные в ходе работы
Рисунок 2.
Изображение двух синусоид на одном
графике (задание №1 – применение функции
hold on)
Рисунок 3.
Изображение двух синусоид на разных
графиках (задание №2– применение
функции subplot)
Рисунок 4.
Иллюстрация эффекта наложения,
полученного в результате нарушения
теоремы Котельникова (слишком низкая
частота дискретизации)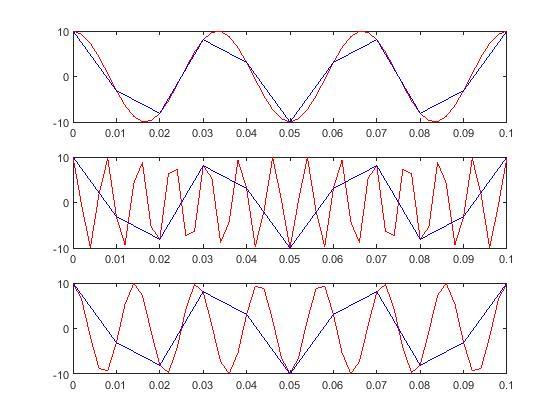
Рисунок 5. Исходный
сигнал ЭКГ (сверху), прореживание
исходного сигнала ЭКГ с коэффициентом
прореживания К1=2(в середине), прореживание
исходного сигнала ЭКГ с коэффициентом
прореживания К2=25 (снизу).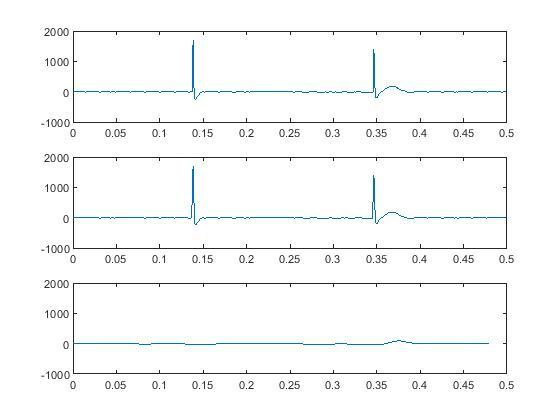
-
Выводы
Любой «природный» сигнал является непрерывным, поэтому для обработки аналоговых сигналов необходимо перейти к цифровому сигналу, в результате чего происходит потеря информации. Актуальной задачей обработки сигналов является описание аналоговых сигналов с наивысшей точностью. Добиться удовлетворительных результатов при оцифровке можно, если следовать теореме Котельникова.
На примере синусоиды частотой F=30Гц, взятой с частотами дискретизации Fs1=500Гц, Fs2=100Гц и соответствующими интервалами дискретизации Т1=1/Fs1, T2=1/Fs2 рассмотрели эффект наложения при нарушении теоремы Котельникова. В качестве частоты сигнала брали F, F+Fs2, Fs2-F, для частоты дискретизации 100Гц наблюдали эффект наложения: все три синусоиды с разными частотами на графике выглядели идентично, так как для частот сигнала F+Fs2, Fs2-F частота дискретизации равная 100Гц не удовлетворяет теореме Котельникова.
Сигнал с дискретной частотой 500Гц при частотах сигнала F, F+Fs2, Fs2-F удовлетворяет теореме Котельникова – наложения не произошло и мы наблюдали 3 разных графика.
Провели исследование эффекта наложения на сигнале ЭКГ. Убедились в том, что возможно сохранить достоверный вид сигнала при уменьшении частоты дискретизации и потере определенного количества информации (Рисунок 5. Прореживание исходного сигнала ЭКГ с коэффициентом прореживания K1=2), но при недостаточной частоте дискретизации происходит значительная потеря информации, которая сильно искажает исходный сигнал (Рисунок 5. Прореживание исходного сигнала ЭКГ с коэффициентом прореживания K2=25).
