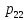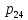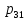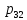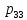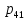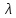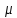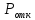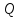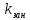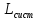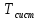Лаба 3 (Цепи Маркова и СМО) / Отчет 2

Цель работы: изучить методы создания и анализа цепей Маркова.

1. ЦЕПЬ МАРКОВА

1. 1. Исходные данные.

Таблица 1. Коэффициенты в матрице переходных вероятностей

Вариант
6	5	5	0	0	0	5	5	0

Вариант
6	0	3	3	0	0	0	3	3

1. Сгенерируем матрицу переходов Р

P=[5,5,0,0;0,5,5,0;0,3,3,0;0,0,3,3];

2. Для создания цепи Маркова, полученной на основе матрицы переходов, воспользуемся функцией dtmc(), задав название состояний “Healthy”, “Unwell”, “Sick”, “Verysick”.

MC=dtmc(P,'StateNames',["Healthy" "Unwell" "Sick" "Very sick"]);

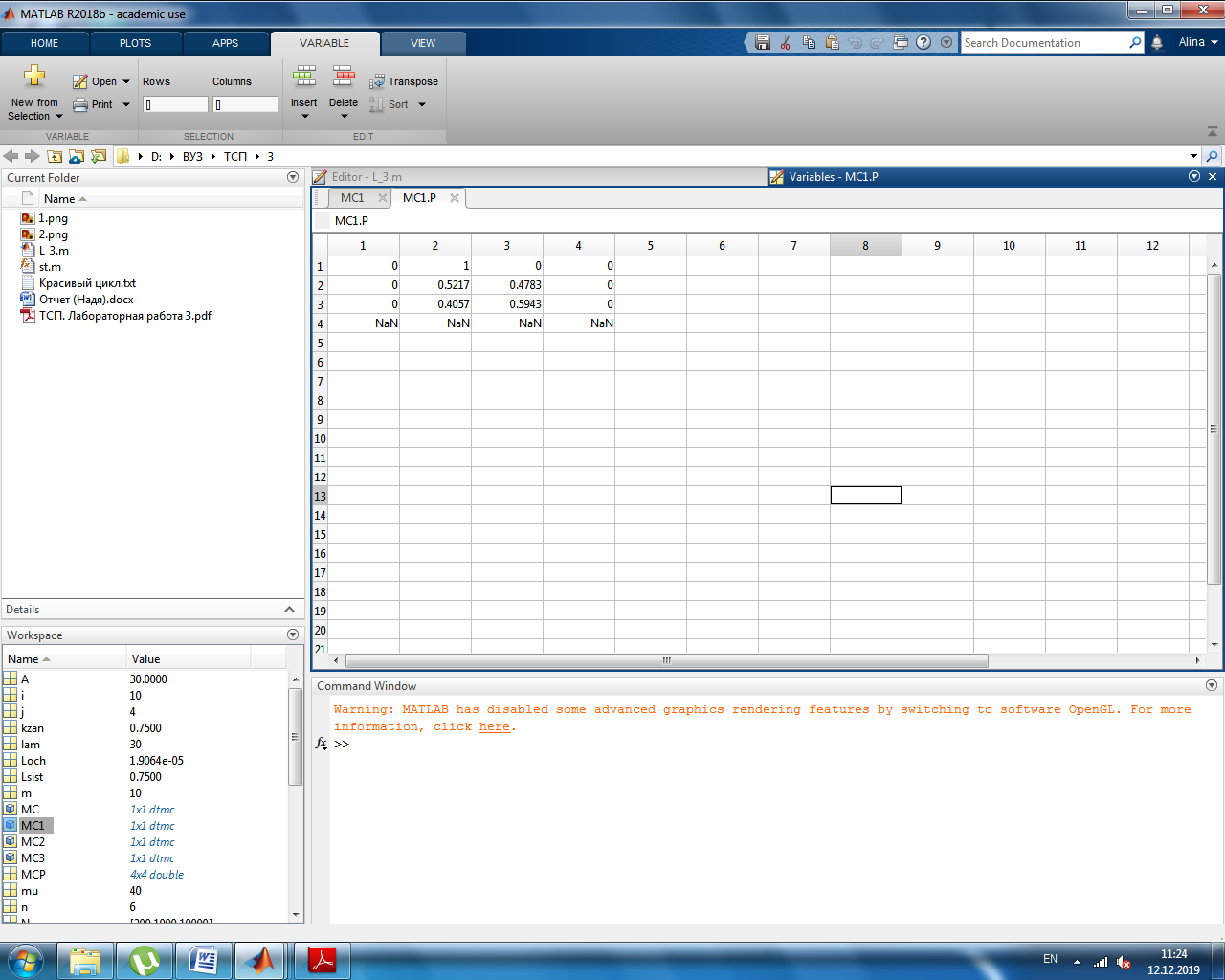
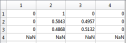
3. Получение нормированной матрицы перехода. Вызвав матрицу переходов полученной цепи, мы получим автоматически нормированную матрицу переходов

MCP=MC.P;

s=sum(MCP,2);

Полученная нормированная матрица переходов представлена на рисунке 1.

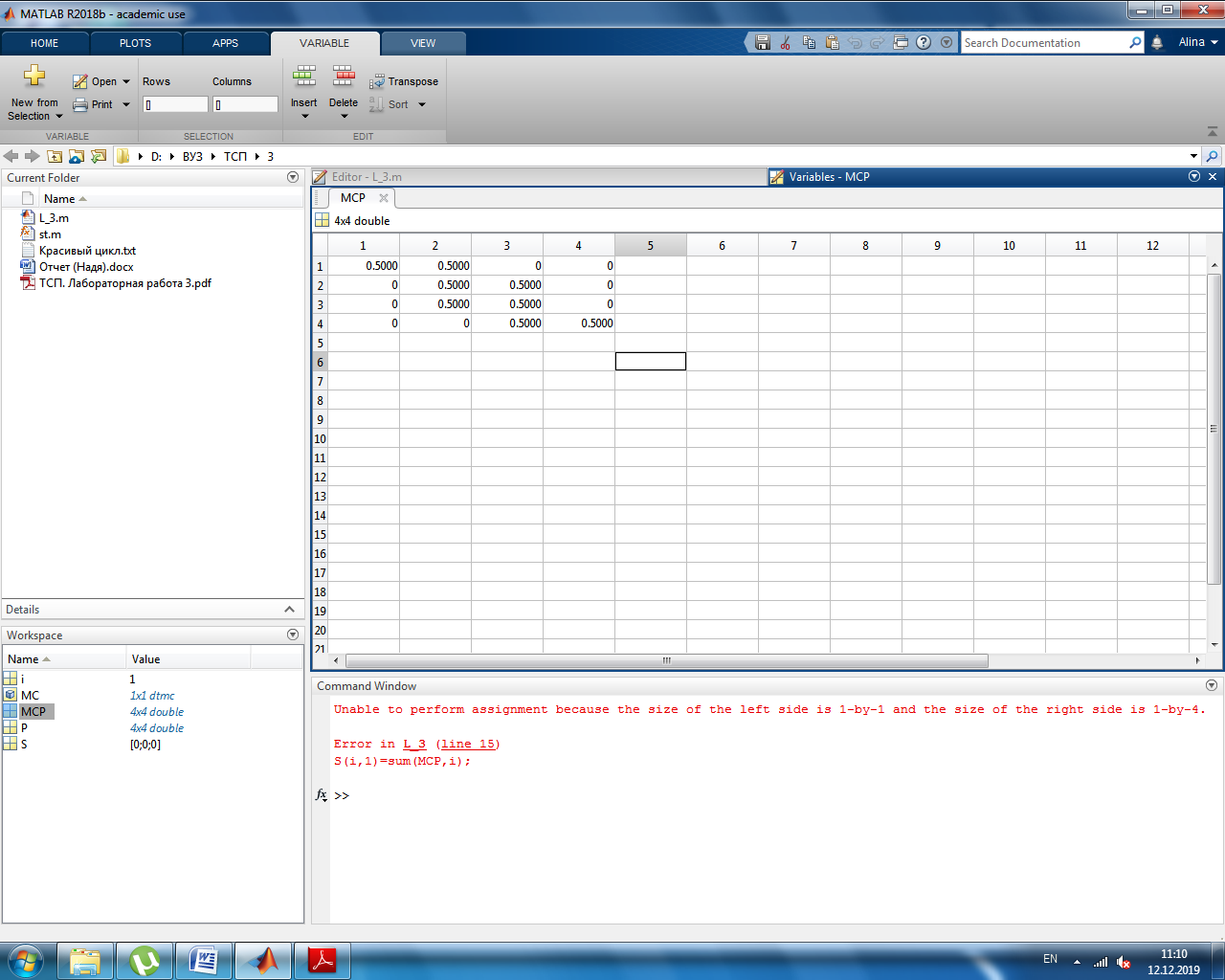
Рисунок 1. Нормированная таблица пеерходов

4. Построение графа цепи Маркова.

figure()

graphplot(MC,'ColorEdges',true);

Рисунок 2. Граф матрицы переходов

5. Построение кумулятивной матрицы переходов

P_cum = MCP;

for K = 1:4

for L=1:3

P_cum(K,L+1) = P_cum(K,L) + P_cum(K,L+1);

end

end

clear K L

6. Моделирование поведения цепи Маркова и построение графика, показывающего, как в течение наблюдений менялось состояние, в котором находилась цепь.

Для моделирования поведения цепи Маркова в течении разного количества итераций (200, 1000, 10000) воспользуемся следующим выражением:

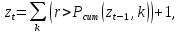
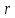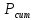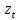где - случайное число, распределенное равномерно на интервале [0,1]; –кумулятивная матрица переходов, и 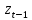- состояние цепи в момент времени и соответственно.

В качестве начального состояния цепи, укажем состояние 1 (“Healthy”).

N=[200 1000 10000];

figure('Name','Моделирование поведения цепи Маркова','NumberTitle','off')

for i=1:3

subplot(3,1,i)

text=['Всего ',num2str(N(i)),' положений'];

title(text)

hold on

z = st(N(i),P_cum);

end

Полученные графики представлены ниже.

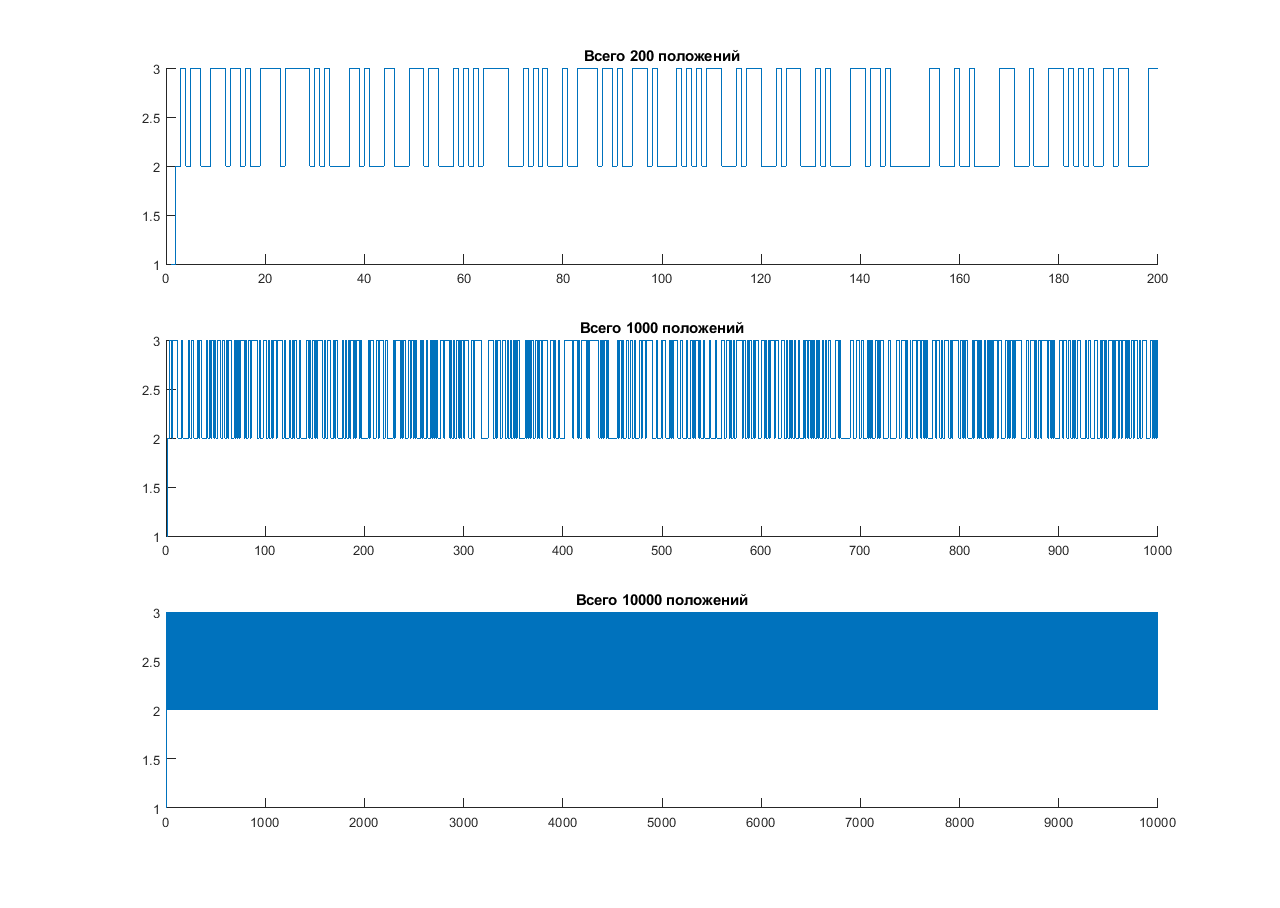
Рисунок 3. Моделирование поведения цепи Маркова

7. Расчёт оценки цепи Маркова по полученным наблюдениям

Расчёт оценки цепи Маркова по полученным наблюдениям производится с помощью выражения:

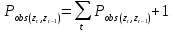
P_obs1=zeros(4,4);

P_obs2=zeros(4,4);

P_obs3=zeros(4,4);

%для 200 иттераций

for n=2:200

for i=1:4

if z(n-1,1)==i

for j=1:4

if z(n,1)==j

P_obs1(i,j)=P_obs1(i,j)+1;

end

end

end

end

end

MC1 = dtmc(P_obs1,"StateNames" , ["Healthy" "Unwell" "Sick" "Very sick"]);

figure('Name','Граф цепи маркова для 200 иттераций','NumberTitle','off')

graphplot(MC1,'ColorEdges',true);

%для 1000 иттераций

for n=2:1000

for i=1:4

if z(n-1,1)==i

for j=1:4

if z(n,1)==j

P_obs2(i,j)=P_obs2(i,j)+1;

end

end

end

end

end

MC2 = dtmc(P_obs2,"StateNames" , ["Healthy" "Unwell" "Sick" "Very sick"]);

figure('Name','Граф цепи маркова для 1000 иттераций','NumberTitle','off')

graphplot(MC2,'ColorEdges',true);

%для 10000 иттераций

for n=2:10000

for i=1:4

if z(n-1,1)==i

for j=1:4

if z(n,1)==j

P_obs3(i,j)=P_obs3(i,j)+1;

end

end

end

end

end

MC3 = dtmc(P_obs3,"StateNames" , ["Healthy" "Unwell" "Sick" "Very sick"]);

figure('Name','Граф цепи маркова для 10000 иттераций','NumberTitle','off')

graphplot(MC3,'ColorEdges',true);

Таблица 3. Матрицы переходов и графы для четырех цепей

Цепи Маркова	Матрица переходов	Граф цепи
MC
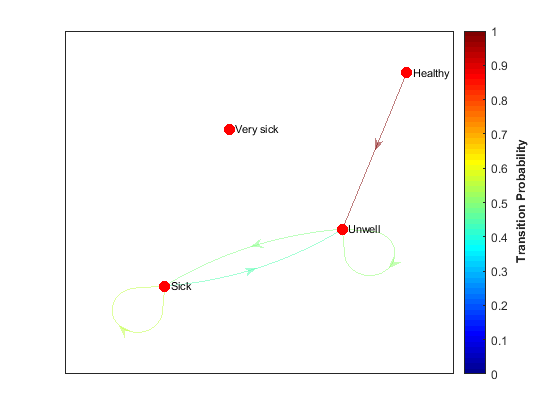
MC1
MC2
MC3

Видно, что с увеличением числа итераций коэффициенты перехода для приближаются к определенной величине. Состояния 1 и 4 постепенно перестают проявляться, так как вероятность переходов из других состояний в данные равен 0. Вероятности перехода между 2 и 3 процессами уравнивается.

8. Теоретические расчеты

Воспользуемся свойством матрицы переходов:

,

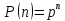где Р – вероятность состояния через n шагов, 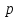– матрица переходных вероятностей.

P1(:,:)=MCP(:,:)^200;

P2(:,:)=MCP(:,:)^1000;

P3(:,:)=MCP(:,:)^10000;

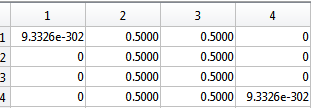
Рисунок 4. Матрицы перехода при 200, 1000, 10000 итераций соответственно, полученные теоретически.

По полученным результатам можем сказать, что полученные моделированием результаты крайне близки к теоретическим.

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра БТС

отчет

по лабораторной работе №3

по дисциплине «Теория случайных процессов»

Тема: ЦЕПИ МАРКОВАИ СИСТЕМЫ МАССОВОГООБСЛУЖИВАНИЯ

		Исаков А.О.
Студенты гр.7501		Попадьина А.О.
Преподаватель		Пустозеров Е.А.

Санкт-Петербург

2019

СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ

1. Исходные данные.

Исходные данные представлены в Таблице 4.

Таблица 4. Характеристики системы массового обслуживания

Вариант			n	m
6	30	40	6	10

lam=30;

mu=40;

n=6;

m=10;

2. Расчет ключевых показателей эффективности СМО

Ключевые показатели эффективности СМО вычисляются по формулам:

• Вероятность отказа ()

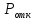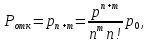
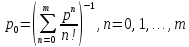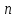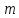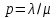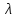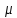где ; –количество каналов; - длинна очереди; ; –интенсивность потока заявок; –интенсивность обслуживания канала.

• Относительная пропускная способность (Q)

• Абсолютная пропускная способность системы (A)

В MATLABэти величины считается следующим образом:

p=lam/mu;

Psum=0;

for i=0:m

Psum=Psum+(p^i)/(factorial(i));

end

p0=Psum^(-1);

Potk=(p^(n+m))*p0/((n^m)*factorial(n));

Q=1-Potk;

A=lam*Q;

Результаты представлены в Таблице 5.

3. Расчёт других показателей СМО

Другие показатели эффективности СМО вычисляются по формулам:

• Среднее количество занятых каналов ()

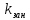• Средняя длина очереди ()

• Среднее время ожидания заявки в очереди ()

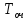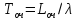
• Среднее количество заявок в системе ()

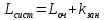
• Среднее время пребывания заявки в системе ()

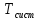В MATLABэти величины считается следующим образом:

kzan=A/mu;

Loch=(p^(n+1))*(1-((p/n)^m)*(m+1-m*p/n))*p0/(n*factorial(n)*(1-p/n)^2);

Toch=Loch/lam;

Lsist=Loch+kzan;

Tsist=Lsist/lam;

Результаты представлены в Таблице 5.

Таблица 5. Показатели эффективности СМО

Показатель	Значение
	1,088*10-13
	1
	30
	0,75
	1,906*10-5
	6,355*10-7
	0,75
	0,025

Проанализировав полученные значения показателей, можно сделать вывод, что система эффективна, т.к. вероятность, что заявка покинет СМО не обслуженной стремится к нулю и, как следствие относительная пропуская способность 1. Также абсолютная пропускная способность системы равна интенсивности потока заявок, что свидетельствует об эффективности системы.

Дополнительные показатели также подтверждают эффективность системы, например средние длина и время ожидания заявки в очереди практически равны нулю, что говорит о сиеминутном начале обработки заявок системой.

Выводы

1. Для цепей Маркова были получены матрицы переходов, графы и промоделированы изменения состояний системы при различном числе итераций: 200, 1000, 10000. Полученные моделированием результаты сходятся с теоретическими расчётами. Система из цепи с 4 состояниями переходит в систему с 2-мя состояниями.

2. Для систем массового обслуживания были рассчитаны ключевые и дополнительные показатели эффективности. Ряд показателей, таких как вероятность отказа, равная нулю, относительная пропускная способность, равная единице и абсолютная пропускная способность, равная интенсивности потока, указывают на крайне высокую эффективность смоделированного СМО. Так же крайне малым оказалось время ожидания в очереди и длина очереди, что говорит о том, что заявка практически сразу поступает в канал.