Баланс мощностей.

Баланс мощностей по сути отображает закон сохранения энергии в электрической цепи. Он предполагает равенство мощности, развиваемой источниками энергии данной цепи, и мощности, потребляемой всеми приемниками этой же цепи. Напомним, что мощность, развиваемая источником ЭДС на участке цепи ab, определяется как 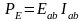, а источника тока . Величина мощности положительна в случае, если знаки сомножителей совпадают, т.е. направление действия источника и тока (напряжения) в ветви совпадают. При противоположных направлениях мощность источника отрицательна. Таким образом, при составлении баланса мощностей сумма мощностей, развиваемых источником, является величиной алгебраической. Сумма мощностей, потребляемых приемниками, является арифметической: .

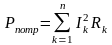Для примера составим баланс мощностей для цепи, приведенной на рис.2.10 :

.

Баланс мощностей обычно составляется для проверки правильности решения электротехнических задач.

Линейные электрические цепи переменного тока — это линейные электрические цепи, в которых напряжения, токи, ЭДС являются произвольными функциями времени (т.е. сигналами).

Применительно к переменным электрическим сигналам , , введены следующие основные понятия.

Мгновенное значение сигнала — значение сигнала в рассматрив момент времени. Обозначается малыми буквами: i, u, e .

Периодический сигнал а(t) — это сигнал, мгновенное значение которого повторяется через равные промежутки времени (см.рис.3.1). Период сигнала Т — это наименьший интервал повторения сигнала. Для периодического сигнала справедливо .

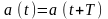Частота периодического сигнала f — величина, обратная периоду , которая равна количеству периодов в секунду (рис.3.1). Единица измерения частоты — Герц : .

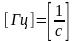Частотная характеристика (ЧХ) — функциональная зависимость какого-либо параметра цепи от частоты. Например: , .

В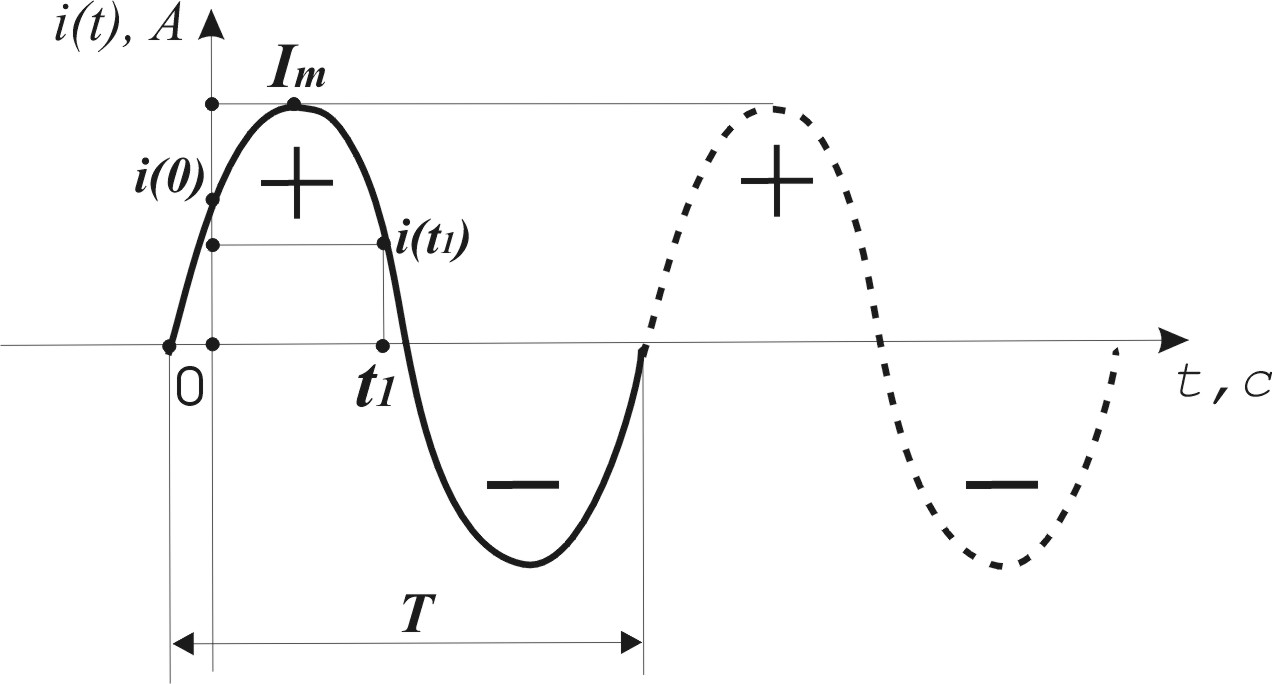 электроэнергетике, системах связи, радио и телевидения наиболее часто применяются простые гармонические сигналы, т.е. токи, напряжения, ЭДС, мгновенные значения которых изменяются по синусоидальному закону (рис.3.2), т.е. направление тока или напряжения периодически изменяется (+/-) .

Для примера запишем закон изменения синусоидального тока (рис.3.2):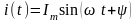 , 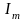— мах значение (амплитуда) тока;

— общая фаза тока (аргумент), которая определяет величину и знак мгновенного значения тока;

— круговая частота (скорость изменения cигнала), .

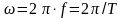радианах в секунду;

— начальная фаза тока (значение фазы тока в момент ).

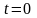Таким образом, общая фаза определяет изменение знака сигнала, а начальная фаза определяет значение сигнала при (рис.3.3).

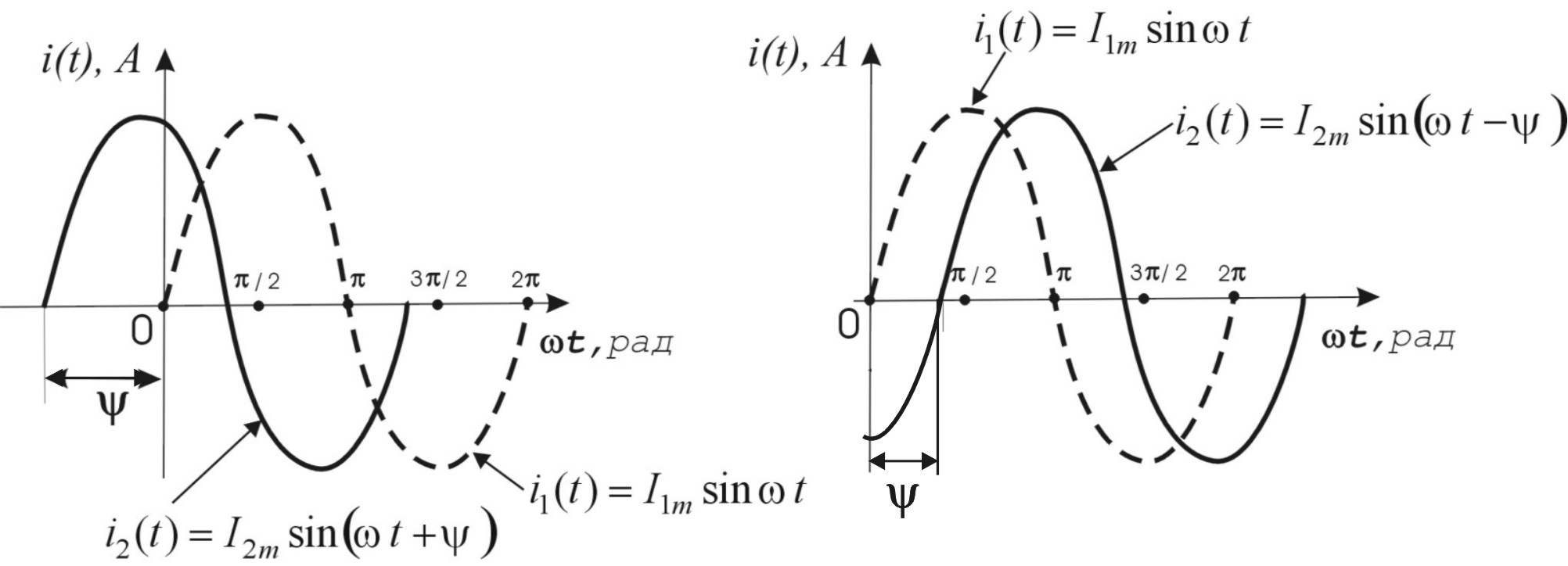
Начальная фаза отсчитывается от точки перехода синусоиды из области отрицательных значений в область положительных (рис.3.3). Положительной начальной фазе соответствует смещение (сдвиг) синусоиды влево от начала координат (рис.3.3а), а отрицательной начальной фазе — сдвиг синусоиды вправо (рис.3.3б). Если два синусоидальных сигнала одинаковой частоты совпадают по фазе (т.е. сдвиг фаз отсутствует), их называют синфазными, если между ними существует сдвиг фаз , они находятся в противофазе.

Действующее значение синусоидального электрического сигнала — это среднеквадратичное значение сигнала за период. Действующее значение является энергетической характеристикой сигнала. Обозначается большими буквами I, E, U :

, , .

Если сравнить тепловой эффект (т.е. количество тепла, выделяемого на резисторе) от постоянного и переменного тока за время , то окажется, что возникший тепловой эффект равен в том случае, когда значение постоянного тока равно действующему значению переменного тока.

Связь между действующим и максимальным значением синусоидального тока можно установить следующим образом:

; .

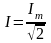Аналогично , .

Акт, ракт, полное сопр.

Оаш

Представление синусоидальной функции комплексным числом. Вращающийся вектор, изображающий синусоидальную функцию, можно описать комплексным числом. Для этого нужно расположить вектор в комплексной плоскости

П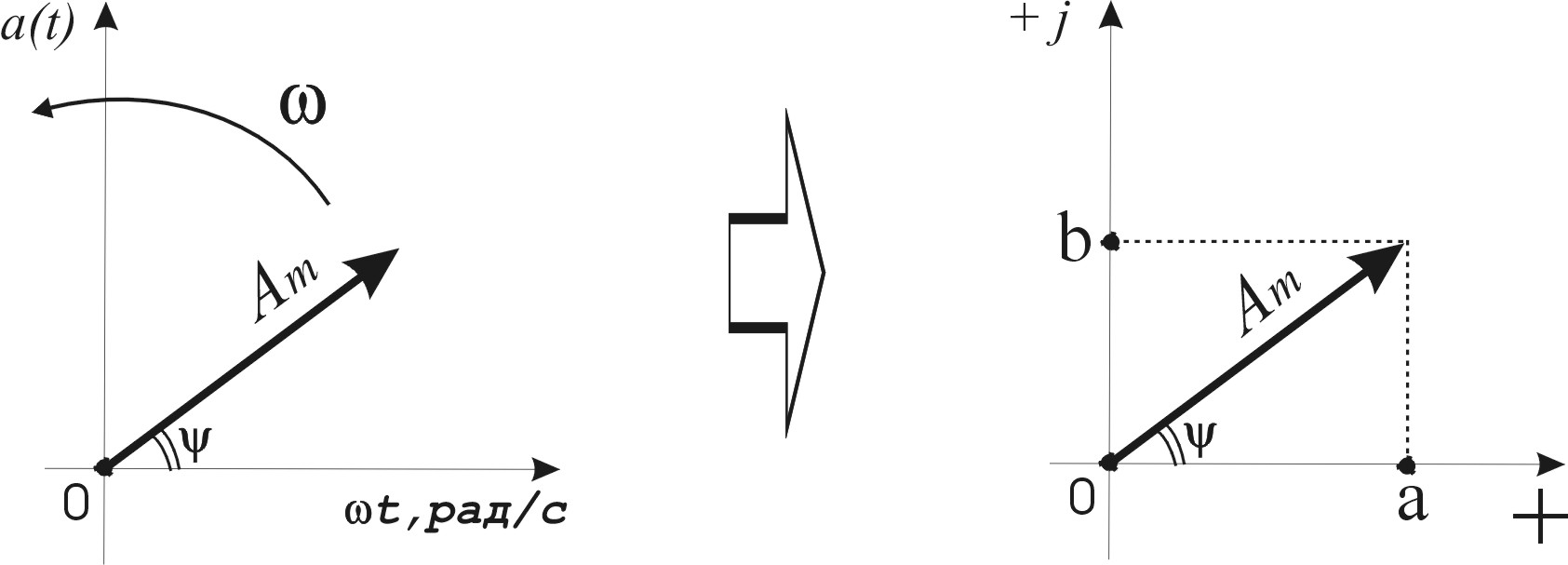 редставление вращающегося вектора комплексным числом дает возможность заменить геометрич действия над векторами алгебраическими действиями над соответств комплексными числами.

Пусть в начальный момент вектор неподвижен тогда его можно представить комплексным числом ,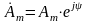

— модуль комплексного числа 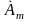(всегда положителен);

— аргумент комплексного числа (имеет любой знак);

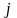— мнимая единица или оператор поворота на 90⁰, .

Для любого момента 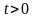вращающемуся вектору соответствует комплексное число ,

где — оператор поворота вектора с круговой частотой ω.

В электротехнике при описании гармонического сигнала величину называют комплексной амплитудой, а величину — комплексной гармонической функцией. Величина 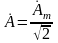называется комплексным действующим значением.

Формы записи комплексных величин. В зависимости от поставленной задачи анализа и расчета цепей синусоидального тока применяются различные формы записи комплексных величин.

Амплитуда (модуль) и фаза (аргумент) определяют показательную форму записи комплексного числа : ,

а также тригонометрическую форму записи: .

Проекции вектора на «действительную» и «мнимую» оси комплексной плоскости (величины и ) определяют алгебраическую форму записи комплексного числа : .

При выполнении действий с комплексными числами зачастую приходится менять форму их записи. Для этого сущ формулы перехода

; ; ; ; .

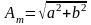Сложение и вычитание комплексных чисел удобно производить в алгебраической форме, а умножение, деление и возведение в степень — в показательной.