Первый и второй законы Кирхгофа

Первый закон Кирхгофа. Алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю:

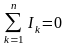,где п — количество ветвей, подключенных к узлу.

Т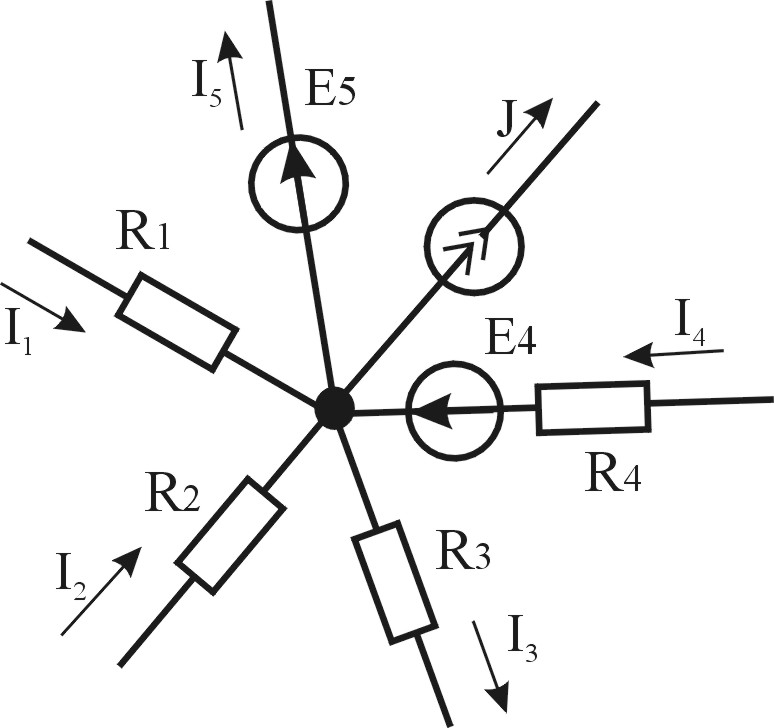 оки, направленные к узлу, входят в сумму со знаком «+», от узла — со знаком «-». Этот закон можно сформулировать и следующим образом: сумма токов, входящих в узел, равна сумме токов, выходящих из узла. Это подтверждает физическую закономерность: в узле не должно происходить накопления зарядов.

Применительно к фрагменту цепи, приведенному на рис.2.4, первый закон Кирхгофа запишется так:

либо .

Если в ветви есть источник тока, то ток ветви равен току этого источника.

Второй закон Кирхгофа. Алгебраическая сумма напряжений на всех ветвях рассматриваемого контура равна нулю:

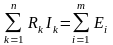.(1) (2)

(2)Другая формулировка: Алгебраическая сумма падений напряжений на всех сопротивлениях данного контура равна алгебраической сумме ЭДС, действующих в контуре:

Знак падения напряжения и ЭДС сопоставляется с направлением обхода контура. Падение напряжения записываются со знаком «+» при совпадении направления тока в соответствующей ветви с выбранным направлением обхода контура, со знаком «-» при противоположных направлениях. ЭДС принимаются положительными при совпадении их направления с направлением обхода контура.

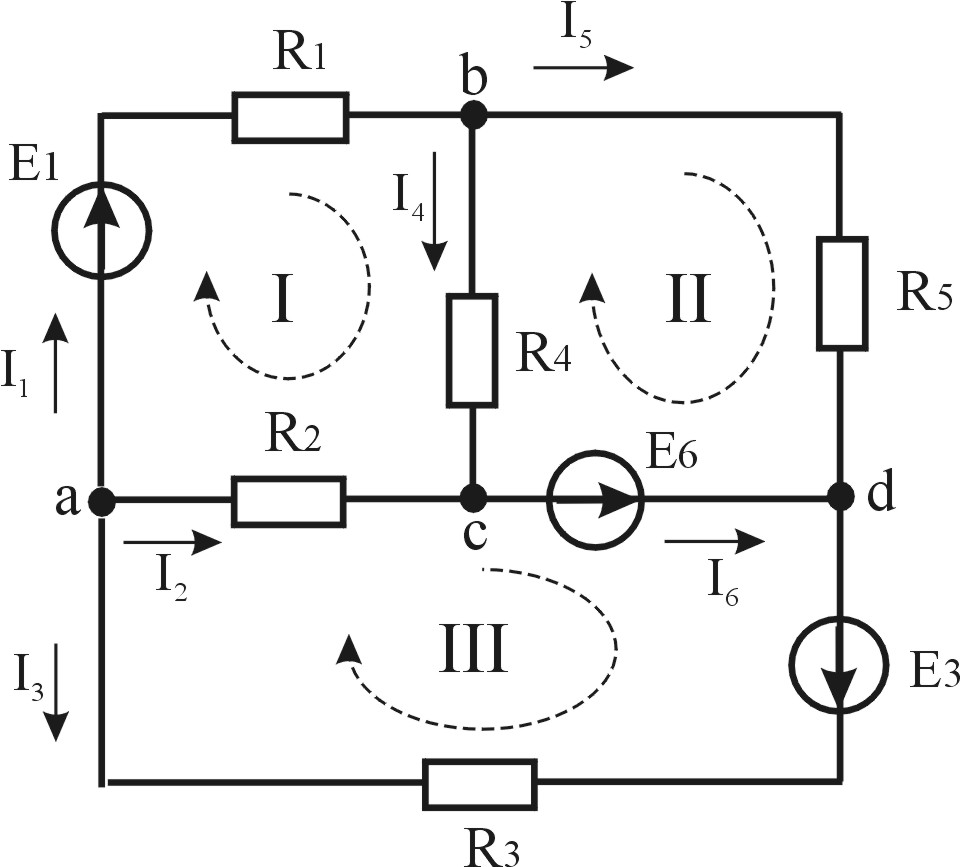
З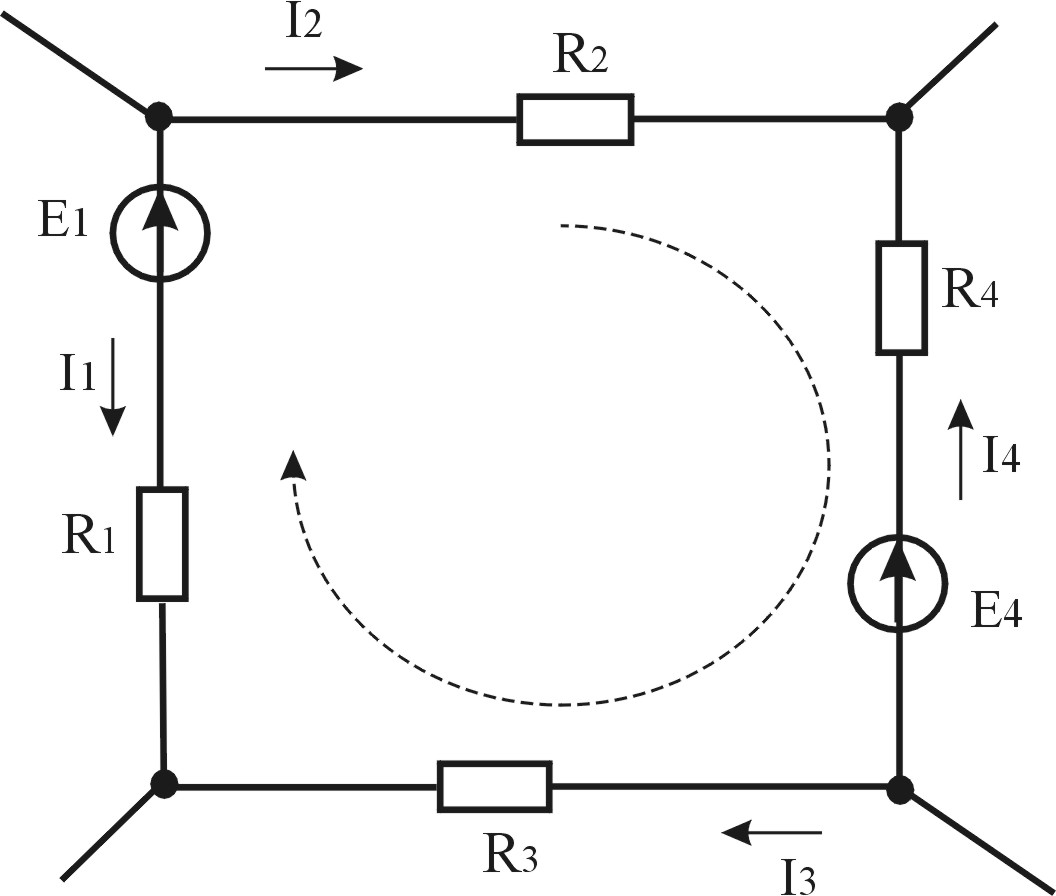 апишем ур-ние по второму закону Кирх применительно к контуру, приведенному на рис.2.5. В соответствии с выбранным направлением обхода контура токи I₂ и I₃ , а значит, и падения напряжения на сопротивлениях R₂ и R₃ входят в левую часть уравнения со знаком «+» ; падения напряжения на сопротивлениях R₁ и R₄ входят в левую часть уравнения со знаком «-».

В правую часть запишем алгебр сумму ЭДС. Направление ЭДС Е₁ и обхода контура совпадают (знак ЭДС «+»), а ЭДС Е₂ — противопол обходу (знак ЭДС «+») :

Если хотя бы в 1 ветвь контура входит идеальный ист.тока, то ур-ние по 2 закону Кирх не может быть составлено, (разрыв в контуре).

Схема электрической цепи, ее топологические элементы

Электрическая цепь — совокупность устройств (элементов, служащих для передачи, распределения или преобразования электромагнитной энергии в цепи), процессы в которых могут быть описаны с помощью понятий тока, напряжения, электродвижущей силы (ЭДС).

Элементы электрической цепи — устройства, входящие в состав цепи и выполняющие в ней определенную функцию. Основными идеализированными элементами электрических цепей являются активные элементы (или источники, вносящие энергию в цепь) и пассивные элементы (или приемники, преобразующие или накапливающие энергию в цепи).

Графическое изображение модели реальной цепи называется схемой замещения или просто схемой (рис.1.1). Она отображает как количество и характер элементов, так и их взаимосвязь в цепи. Топологическими элементами схемы являются ветвь, узел, контур.

Ветвь — это участок цепи, содержащий один либо несколько соединенных друг за другом элементов. При этом вдоль одной ветви протекает один и тот же ток.

Узел — это точка соединения трех и более ветвей.

Контур — это некоторый замкнутый путь вдоль ветвей и узлов схемы. Простейшая цепь состоит из одного контура. На практике чаще рассматриваются многоконтурные схемы.

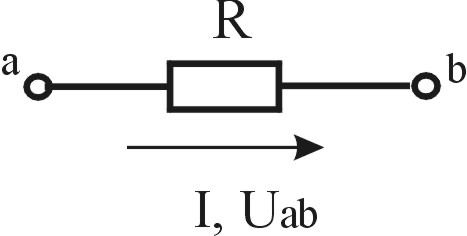
Закон Ома для пассивной и активной участка цепи

Закон Ома. Закон Ома применительно к пассивной ветви имеет вид (рис.2.1а): 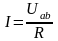,а для активной ветви (рис.2.1б) :

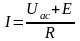
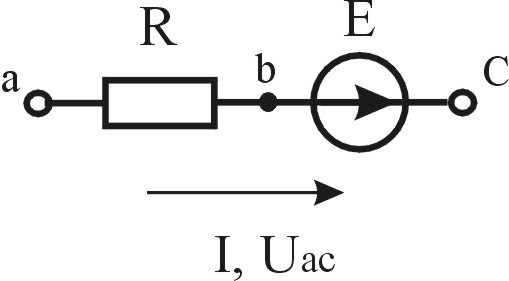
Если на схеме (рис.2.1б) ЭДС направить навстречу току, то . Обобщен. з-н Ома для участка цепи ав:

! !

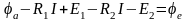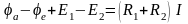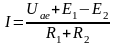
Закон Ома для замкнутой одноконтурной цепи :

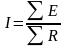
Эквивалентные преобразования электрических цепей. Определение эквивалентного сопротивления.

Метод состоит в эквивалентной замене всей электрической цепи или сложных ее частей более простыми по структуре участками. При этом токи и напряжения в непреобразованной части цепи не должны изменяться. Преобразование цепи приводит к значительному упрощению ее расчета.

Замена последовательного соединения резистивных элементов одним эквивалентным. Простейшим видом соединения является последовательное соединение, когда n элементов соединены друг за другом (один вывод предыдущего соединен с одним выводом последующего). В результате получается участок с двумя крайними выводами а и b (двухполюсник), вдоль которого протекает ток, общий для всех элементов (рис.2.6). Напряжение на участке аb при последовательном соединении равно сумме падений напряжений на отдельных эл-тах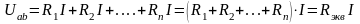

где 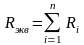— эквивалентное сопротивление последов соединения.

Замена параллельного соединения резистивных элементов одним эквивалентным. При параллельном соединении все п элементов подключены к одной паре узлов а и b, таким образом общим для всех элементов является напряжение 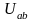, которое равно разности потенциалов в узловых точках. Входной ток распределяется по п параллельным ветвям, в которых величины токов определяются по закону Ома (рис.2.7): .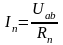

Ток в неразветвленной части цепи определяется по первому закону Кирхгофа как .

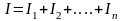Учитывая условие эквивалентной замены, при подстановке получим :

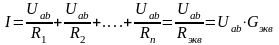,откуда можно определить эквив сопротивление или проводимость параллельного участка цепи: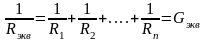 .В частном случае при параллельном соединении двух резисторов получаем: .

Взаимная замена цепи резистивных элементов, соединенных треугольником и звездой. В разветвленных цепях встречаются соединения элементов, которые нельзя отнести к последовательному или параллельному соединению. К таким соединениям относится трехлучевая звезда (рис.2.8а) и треугольник (рис.2.8б) сопротивлений. Условием эквивалентной замены является сохранение значений входных токов І_a , I_b , I_c и потенциалов в точках a , b , c .

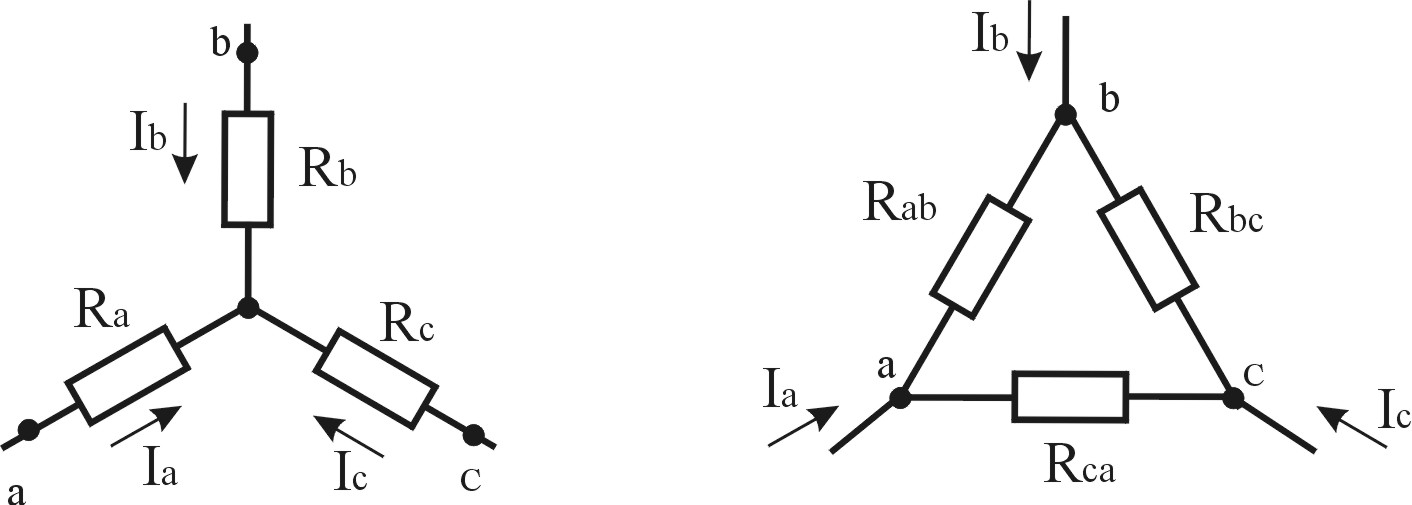
Формулы преобразования треугольника сопротивлений в эквивалентную звезду:

; ; .

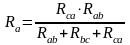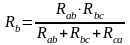Формулы преобразования звезды сопротивлений в эквивалентный треугольник:

; ;

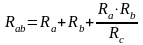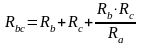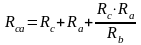
Метод наложения

Метод наложения (МН) основан на применении пр-па суперпозиции (наложения). При наличии в цепи более 3х источников расчеты усложняются, поэтому применение этого метода становится нерац.

Принцип наложения. Реакция цепи на сумму воздействий равна алгебраической сумме реакций на каждое из воздействий в отдельности.

Под реакцией цепи понимается ток, а под воздействием — действие источников ЭДС или тока. Таким образом, ток в каждой ветви схемы, возникающий под действием всех источников, можно представить как алгебраическую сумму частичных токов этой ветви, вызванных действием каждого источника в отдельности.

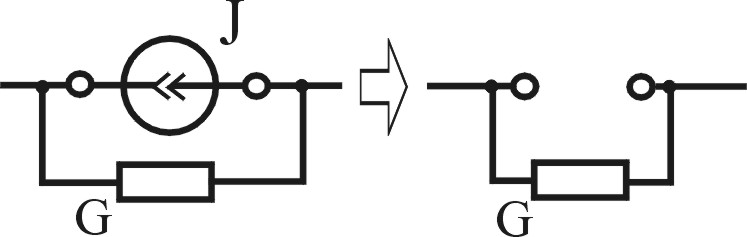
1. Определение количества источников в цепи и составление расчетных схем. При расчете цепей по МН нужно сначала составить расчетные схемы, количество которых равно количеству источников в цепи. В каждой из расчетных схем остается только один из источников, а остальные источники «устраняются» таким образом, что вместо реальных источников в схеме остаются их внутренние сопротивления, идеальный источник ЭДС заменяется перемычкой, а идеальный источник тока — разрывом (табл.2.1).

2. Определение частичных токов по расчетным схемам.

Расчетные схемы, как правило, оказываются простыми, поэтому определить частичные токи по ним несложно. Обычно достаточно применить метод преобразования цепи, формулы разброса. В этом преимущество метода наложения.

3. Нахождение тока в каждой ветви исходной схемы как алгебраической суммы частичных токов. Знаки частичных токов в алгебраической сумме определяются сопоставлением их направлений с направлениями токов в исходной схеме.

Метод законов Кирхгофа

Метод законов Кирхгофа (МЗК) является наиболее общим методом расчета электрических цепей. Он основан на решении системы уравнений, составленных по первому и второму законам Кирхгофа относительно реальных токов в ветвях рассматриваемой цепи. Общее количество уравнений должно быть равно числу неизвестных токов (т.е. числу ветвей схемы, не содержащих источников тока).

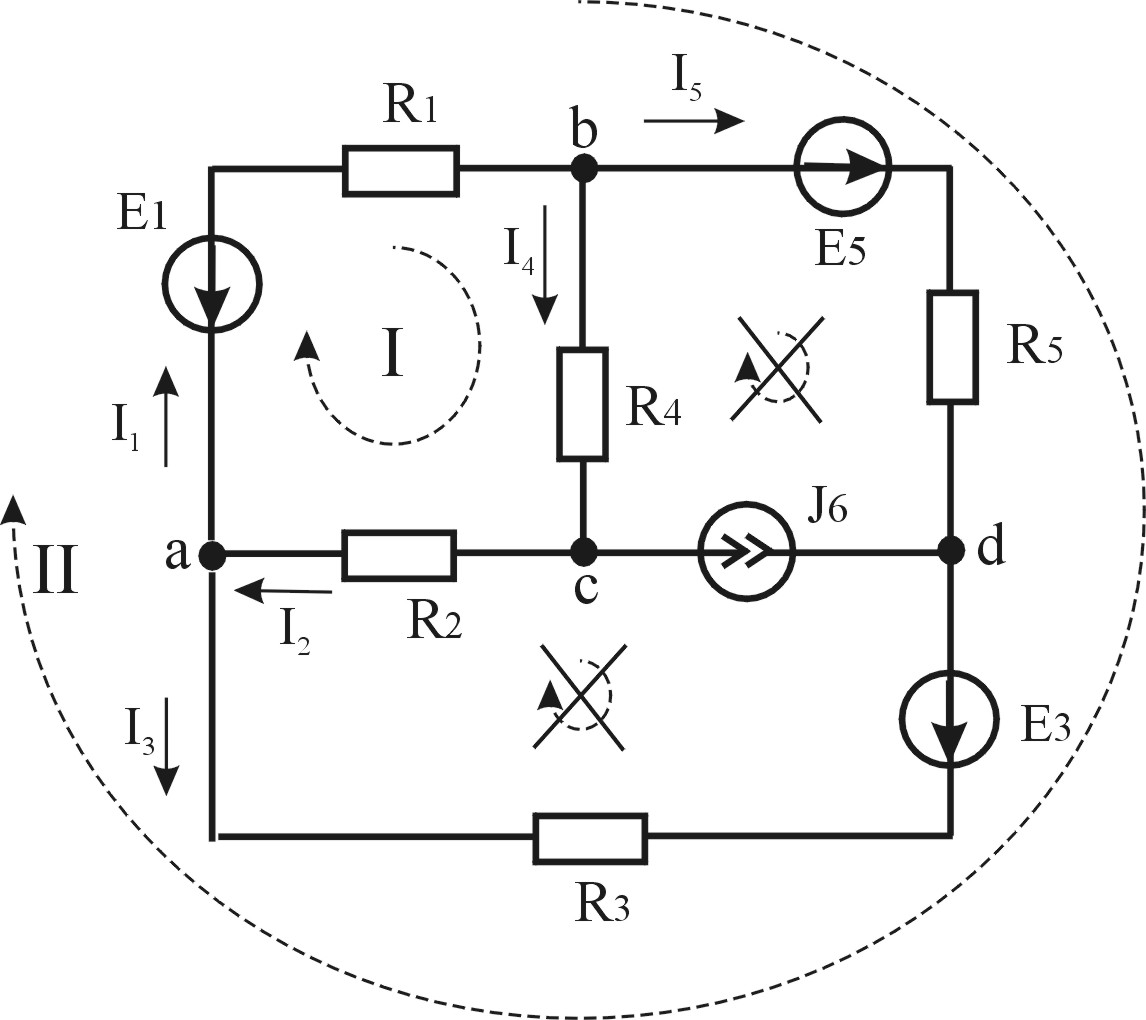
1. Определение количества ветвей схемы p . Если в схеме есть s ветвей с источниками тока, ток в этих ветвях уже известен. Тогда в задаче необходимо определить (p-s) токов. В каждой ветви произвольно выбирают положительное направление тока и обозначают его стрелкой.

Определение количества узлов схемы q.

3. Определение количества независимых контуров схемы m. Оно равно числу ячеек схемы: 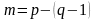. В каждом контуре произвольно выбирают направление обхода и обозначают его стрелкой. Контуры выбирают так, чтобы они не проходили через ветвь с источником тока.

Составление 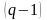уравнений по первому закону Кирхгофа для узлов и уравнений по второму закону Кирхгофа для независимых контуров. Ток источников тока входит только в уравнения по первому закону Кирхгофа. Общее количество расчетных уравнений равно (p-s). Решение системы уравнений сразу дает значения всех искомых токов цепи.

Некоторые из полученных значений токов могут оказаться отрицательными. Это значит, что истинное направление тока в ветви противоположно первоначально выбранному условному направлению.