Лекція № 11. Дискретне операційне числення|обчислення|

1. Дискретне перетворення Лапласа

Дискретне перетворення Лапласа застосовують до так званих гратчастих функцій. Гратчастою функцією називається функція, визначена тільки|лише| для цілих значень аргументу . (вона тотожно рівна нулю при негативних|заперечних| значеннях аргументу).

Функція безперервного аргументу, визначена для всіх , називається функцією, що породжує, для гратчастої функції .

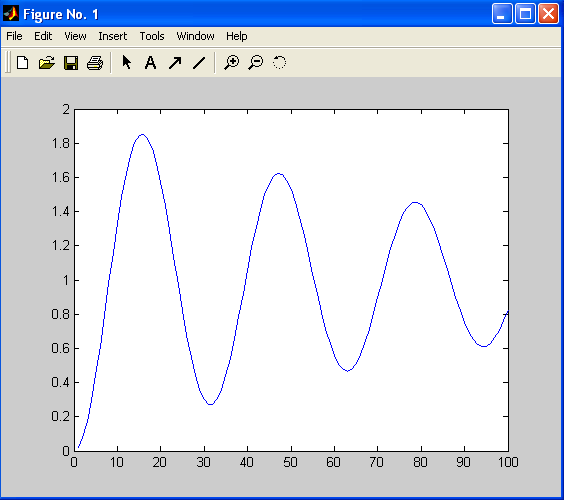
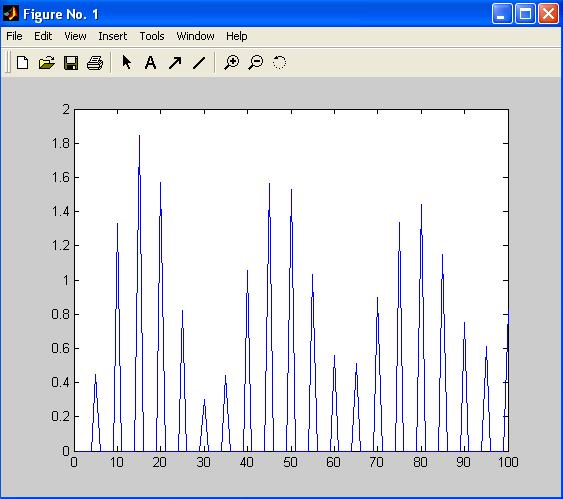
а б

Мал. 11.1. Функція, що породжує (а), і гратчаста функція (б)

Зображенням гратчастої функції є|з'являється,являється| функція, що задовольняє співвідношенню

(11.1)

де – параметр перетворення.

У операторній формі це співвідношення записується|занотовується| таким чином:

.

Перетворення гратчастих функцій відповідно до даного співвідношення називається дискретним перетворенням Лапласа.

Всяка|усяка| функція , для якої існує звичайне|звичне| перетворення Лапласа, породжує гратчасту функцію , для якої, у свою чергу|своєю чергою|, визначено дискретне перетворення Лапласа. Властивості дискретного перетворення Лапласа гратчастої функції, в основному, такі ж, як і для звичайного|звичного| перетворення Лапласа, проте|однак| тут у всіх випадках інтеграли замінюються нескінченними|безконечними| сумами.

Припустимо|передбачимо|, що задана послідовність чисел . Тоді гратчасту функцію можна представити|уявити| у вигляді суми послідовностей імпульсних - функцій Дірака.

.

- функція – це спеціальна (узагальнена) функція, що володіє наступними|такими| властивостями.

, .

Дискретне перетворення Лапласа послідовності – це звичайне|звичне| перетворення Лапласа імпульсної функції :

.

2. Основні теореми дискретного перетворення Лапласа

1. Властивість лінійності: .

2. Теорема зрушення|зсуву|: ,

.

3. Теорема зсуву|зміщення|: .

4. Теорема про диференційованість| по параметру:

.

5. Теорема про множення гратчастої функції на :

.

6. Теорема згортання:

7. Граничні значення гратчастої функції:

,

.

3. z-перетворення

Якщо ввести|запровадити| позначення , то теорема зрушення|зсуву| прийме наступну|таку| форму . Тут – має сенс оператора зрушення|зсуву|, за допомогою якого гратчастій функції ставиться у відповідність та ж функція із|із| зрушеним|зсунутим| аргументом . В цьому випадку дискретне перетворення Лапласа можна представити|уявити| таким чином

. (11.2)

В цьому випадку воно називається z-перетворенням. Це перетворення практично співпадає|збігається| з|із| дискретним перетворенням Лапласа і відрізняється тільки|лише| аргументом зображення. При такій заміні трансцендентні функції від аргументу q перетворяться в раціональні функції від аргументу z.

Відшукання|відшукування| оригіналів по зображеннях для дискретного перетворення Лапласа і z-перетворення проводиться|виробляється,справляється| по формулах, подібних формулах, вживаних у разі|в разі| звичайного|звичного| перетворення Лапласа. У табл. 11.1 приведені деякі формули z-перетворення гратчастих функцій.

Таблиця 11.1

1
n

Приклад|зразок| 11.1. Вирішимо|розв'яжемо| різницеве (рекурентне) рівняння

де

Для цього знайдемо - перетворення цього рівняння

.

Звідси слідує|прямує|

.

Зображення відомої функції можна представити|уявити| у вигляді|виді|

.

Таким чином

Гратчаста функція рівна коефіцієнтам одержаного|отриманого| ряду|лави,низки|

.