5. Біноміальні коефіцієнти

Слово біном означає вираз|вираження|, що складається з двох членів, наприклад: |в,біля|. Біном є|з'являється,являється| окремим випадком полінома. Біномом Ньютона називається біном, піднесений до цілого позитивного ступеня: . Достатньо|досить| легко одержати|отримати| наступні|слідуючі| приватні формули:

,

,

.

У загальному|спільному| випадку формула розкладання для бінома записується|занотовується| наступним чином:

. (4.1)

Символи , де – позначають|значать| цілі позитивні числа, звані біноміальними коефіцієнтами. Тут n – ступінь|міра| полінома, – номер біноміального коефіцієнта.

Теорема 4.1. (Біноміальна теорема) Біноміальні коефіцієнти розраховуються по формулі:

(4.2)

, .

Доказ. Використовуємо метод математичної індукції. Якщо n=1, то , а . Це приводить|призводить,наводить| до вірного виразу|вираження|: . Таким чином, для одиниці дана властивість виконується. Припустимо|передбачимо|, що воно також виконується і для ступеня|міри| n – 1. Тоді справедливо вираз|вираження|:

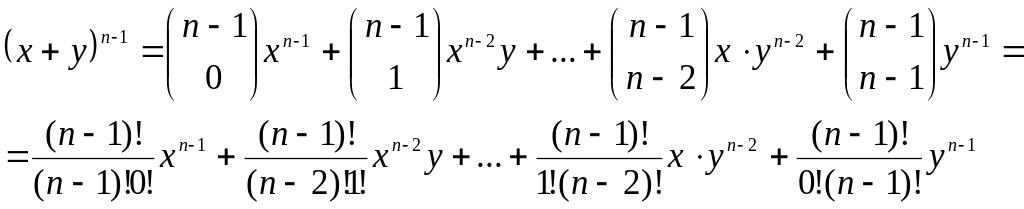
Умножаючи|множивши| цей вираз на (x + у|в,біля|), одержимо|отримаємо|:

Таким чином, теорема доведена.

6. Трикутник Паскаля

Французький математик Блез Паскаль (1623-1662) склав таблицю з|із| біноміальних коефіцієнтів. Вона вийшла трикутною, оскільки із|із| збільшенням ступеня|міри| бінома кількість коефіцієнтів також збільшується. Тому цю таблицю називають трикутником Паскаля. На мал. 4.1 показаний трикутник Паскаля, в якому використані формальні позначення біноміальних коефіцієнтів. На мал. 4.2 приведений трикутник Паскаля з|із| числовими значеннями біноміальних коефіцієнтів.

Цього значення може бути набуте за допомогою формули (4.2). Проте|однак| трикутник Паскаля дає можливість|спроможність| розраховувати біноміальні коефіцієнти без застосування|вживання| даної формули. Якщо відомі коефіцієнти в якому-небудь рядку таблиці, то можна легко обчислити|обчисляти,вичислити| коефіцієнти в сусідньому рядку, який знаходиться|перебуває| нижче першого. Для визначення кожного коефіцієнта нижнього рядку потрібно скласти два коефіцієнти верхнього рядка, які знаходяться|перебувають| зліва|ліворуч| і справа безпосередньо над коефіцієнтом, що розраховується. Таким чином, рухаючись|сунучись| від вершини трикутника вниз, можна послідовно розрахувати біноміальні коефіцієнти для будь-якого кінцевого|скінченного| ступеня|міри| бінома Ньютона.

Мал. 4.1. Трикутник Паскаля

Мал. 4.2. Трикутник Паскаля з|із| числовими значеннями коефіцієнтів

7. Біном Ньютона для дробових і негативних|заперечних| показників

Формула бінома Ньютона (4.1) для цілих позитивних показників була відома задовго до Ісака Ньютона (1643-1727), але|та| їм в 1676 році була вказана можливість|спроможність| розповсюдження|поширення| цього розкладання і на випадок дробового або негативного|заперечного| показника (хоча строге|суворе| обгрунтування цього було дано лише норвезьким математиком Нільсом Хенріком Абелем (1802-1829) в 1826 році).

У цьому, більш загальному, випадку формула бінома Ньютона починається|розпочинається,зачинається| так само, як і формула (4.1), біноміальним коефіцієнтом служить вираз|вираження|:

,

яке у разі|в разі| цілого позитивного n, звертається|обертається| в нуль при всякому |усякому|, унаслідок|внаслідок| чого формула (4.1) містить|утримує| лише кінцеве|скінченне| число членів. У разі ж дробового (або негативного|заперечного|) n всі біноміальні коефіцієнти відмінні|інші| від нуля, і права частина|частка| формули містить|утримує| нескінченний|безконечний| ряд|лаву,низку| членів (біноміальний ряд|лава,низка|). Якщо цей ряд|лава,низка| сходиться, то узявши достатньо|досить| велике число його членів, можна одержати|отримати| величину, скільки завгодно близьку .