Лекція № 3. Множини|безліч| і підмножини
Завдання|задавання| множин|безлічі|
Якщо
об'єкт
є|з'являється,являється|
елементом множини|безлічі|,
то говорять, що
належить
.
Позначення
.
Інакше говорять, що
не належить
.
Позначення
.
Множина|безліч|,
що не містить|утримує|
елементів, називається порожньою|пустим|.
Позначення:
.
Щоб задати множину|безліч|, потрібно вказати, які елементи їй належать. Це можна зробити різними способами.
Переліком|перерахуванням| елементів:
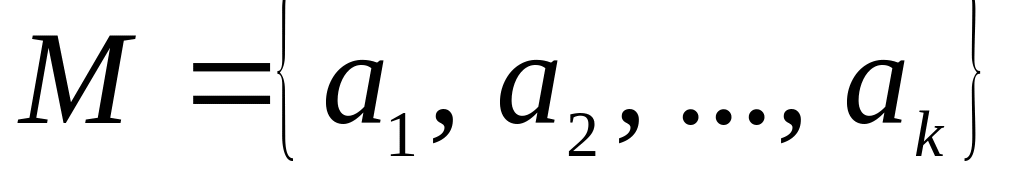.Характеристичним предикатом:
.Процедурою, що породжує:
.
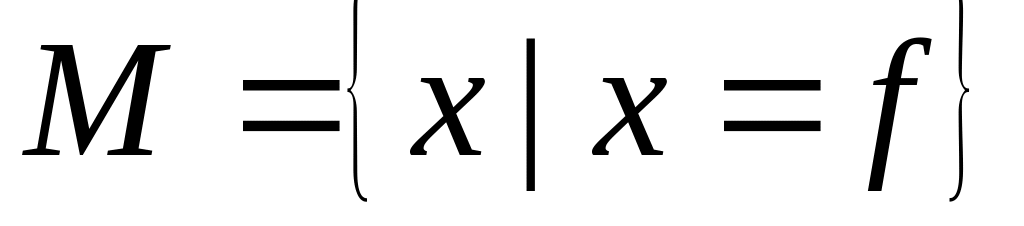При завданні|задаванні| множин|безлічі| переліком|перерахуванням| позначення елементів звичайно беруть у фігурні дужки і розділяють комами. Характеристичний предикат (від латинського praedicatum) – це деяка умова, виражена|виказана,висловлена| у формі логічного твердження|затвердження|, що повертає логічне значення. Якщо для даного елементу умова виконана, то він належить визначуваній множині|безлічі|, інакше – не належить. Процедура, що породжує, – це процедура, яка, будучи запущеною|занедбаною|, породжує деякі об'єкти, що є|з'являються,являються| елементами визначуваної множини|безлічі|.
Приклад|зразок|
3.1. 
;
;
.
Парадокс Рассела
Завдання|задавання|
множин|безлічі|
характеристичним предикатом може
приводити|призводити,наводити|
до суперечностей|протиріч|.
Наприклад, всі розглянуті|розгледіти|
в прикладах|зразках|
множини|безліч|
не містять|утримують|
себе як елемент. Розглянемо|розгледимо|
безліч всіх множин|безлічі|,
що не містять|утримують|
себе як елемент:
.
Якщо
множина|безліч|
існує, то ми повинні мати
можливість|спроможність|
відповісти на наступне|таке|
питання:
?
Хай
|нехай|,
тоді
.
Хай
|нехай|,
тоді
.
Виходить неусувна логічна
суперечність|протиріччя|,
яка відома як парадокс
Рассела.
Існує три способи уникнути цього
парадоксу.
Обмежити використовувані характеристичні предикати виглядом|видом|
де
– відома, свідомо існуюча множина|безліч|
(універсум).
Звичайно при цьому використовують
позначення
.
Для
універсум не вказаний, а тому
множиною|безліччю|
не є|з'являється,являється|.
Теорія типів. Об'єкти мають тип 0, множини|безліч| мають тип 1, безліч множин|безлічі| – тип 2 і т.д. не має типу і множиною|безліччю| не є|з'являється,являється|.
Характеристичний предикат
заданий у вигляді обчислюваної|обчисляти,вичисляти|
функції (алгоритму). Спосіб
обчислення|підрахунку|
значення предиката
не заданий, а тому
множиною|безліччю|
не є|з'являється,являється|.
Останній з|із| перерахованих способів лежить в основі так званого конструктивізму – напряму|направлення| в математиці, в рамках|у рамках| якого розглядаються|розглядуються| тільки|лише| такі об'єкти, для яких відомі процедури (алгоритми) їх породження. У конструктивній математиці виключаються з|із| розгляду деякі поняття і методи класичної математики, чреваті можливими парадоксами.