Набір істиннісних значень 0001 відповідає результатам операцій:

0 & 0 = 0;

0 & 1 = 0;

1 & 0 = 0;

1 & 1 = 1.

Як відомо, в арифметиці спочатку виконуються операції множення або ділення|поділки,розподілу,поділу|, а потім – складання або віднімання. Логічні зв'язки|в'язки| також підкоряються подібному правилу. Пріоритет застосування|вживання| зв'язок|в'язок| зростає в наступному|слідуючому| порядку|ладі|: &, !. Щоб змінити|поміняти| цей порядок|лад|, то, як і в арифметиці, необхідно використовувати дужки.

2. Пропозиціональні змінні і формули

Змінна, значеннями якої є|з'являються,являються| вислови|висловлювання|, називається пропозиціональною| змінною. Поняття пропозиціональної| формули вводиться|запроваджується| по індукції:

1. вираз|вираження|, що складається тільки|лише| з пропозиціональній| змінної, є|з'являється,являється| пропозициональною| формулою;

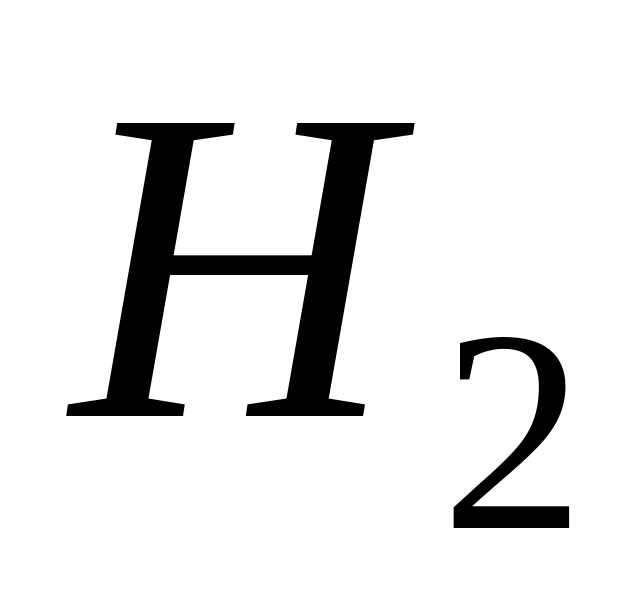2. якщо і – пропозиціональні| формули, то кожний з виразів

, ( ), ( ), ( ) і ( ) – пропозиціональна| формула;

3. послідовність символів тільки|лише| тоді є|з'являється,являється| пропозиціональною| формулою, коли вона побудована|споруджена| відповідно до 1) і 2).

Приклад|зразок| 2.2. Приклади|зразки| пропозиціональних| формул:

,

.

3. Булеві функції

Функція, у|в,біля| якої аргументи пробігають множину|безліч| {0,1} і яка приймає значення з|із| тієї ж множини|безлічі| {0,1}, називається функцією алгебри логіки або булевою функцією.

Особливе значення мають так звані елементарні булеві функції. Двомісними елементарними булевими функціями є|з'являються,являються| кон'юнкція, диз'юнкція, імплікація, сума по модулю 2, эквіваленція|, штрих Шефера і стрільця Пірсу. Символи А1 і А2 з|із| табл. 2.2 слід в цьому випадку тлумачити як булеві змінні {0,1}.

Є|наявний| дві одномісні булеві функції, залежні від x: тотожна функція і заперечення . Це елементарні функції (табл. 2.3).

Таблиця 2.3

x
0	0	1
1	1	0

Є|наявний| дві нуль-місцеві елементарні булеві функції: це константи 0 і 1. Кожній пропозиціональній| формулі можна зіставити булеву| функцію. Булева функція, зіставлена пропозиціональній| формулі Н, називається функцією істинності формули Н.

Хай|нехай| – функція істинності (i =1, 2); хай|нехай| { } – безліч тих змінних, які зустрічаються хоч би в одній з функцій і . Пропозиціональні формули і називаються еквівалентними, якщо на всякому|усякому| наборі ( ) значень змінних значення функцій і співпадають|збігаються| (еквівалентність позначають|значать| як: ).

Основні еквівалентності:

– правило зняття подвійного заперечення;

Н&НН – ідемпотентність| кон'юнкції;

Н Н Н | – ідемпотентність | диз'юнкції;

Н₁*Н₂ Н₂*Н₁ – комутативність зв'язки|в'язки| * (символ * є|з'являється,являється| загальним|спільним| позначенням для зв'язок|в'язок|: &, , );

(Н₁*Н₂)*Н₃ Н₁*( Н₂*Н₃) – асоціативність зв'язки|в'язки| *;

Н₁&( Н₂ Н₃ ) (Н₁ &Н₂) (Н₁ &Н₃) – дистрибутивність («distributivus» – розподільний) кон'юнкції щодо|відносно| диз'юнкції;

Н₁ ( Н₂&Н₃ ) (Н₁ Н₂)& (Н₁ Н₃) – дистрибутивність диз'юнкції щодо|відносно| кон'юнкції;

і – закони де| Моргана;

Н₁ (Н₁&Н₂ ) Н₁ и Н₁ &(Н₁ Н₂ ) Н₁ – закони поглинання;

і

– закон суперечності|протиріччя|;

– закон виключеного третього;

;

;

;

.