Модулярна арифметика
У цьому
розділі всі числа – цілі. Говорять, що
число а
порівнянно
по модулю n
з|із|
числом b
(позначення
),
якщо а
і
b
при
діленні|поділці,розподілі,поділі|
на n
дають
один і той же залишок|остачу|:
.
Відношення|ставлення|
порівнянності
рефлексія,
симетрично і транзитивно і
є|з'являється,являється|
відношенням|ставленням|
еквівалентності. Класи еквівалентності
по відношенню|ставленню|
порівнянності (по модулю n)
називаються вирахуваннями
(по модулю n).
Безліч вирахувань по модулю n
позначається|значиться|
.
Звичайно з|із|
кожного вирахування вибирають одного
представника – ненегативне число, яке
при діленні|поділці,розподілі,поділі|
на n
дає
приватне 0. Це дозволяє вважати|лічити|,
що
,
і спростити позначення.
Над
вирахуваннями (по модулю n)
визначені операції складання і множення
по модулю n,
що позначаються|значаться|
відповідно
і
,
і визначувані таким чином:
, 
.
Якщо з|із| контексту ясно, що мається на увазі операція по модулю n, то індекс n опускається.
Розглянемо|розгледимо|
– підмножина
чисел, взаємно
простих з|із|
n.
Числа називаються взаємно простими,
якщо їх найбільший загальний|спільний|
дільник рівний одиниці. Для чисел з|із|
множини|безлічі|
існують зворотні числа по відношенню
до операції множення по модулю n.
Приклад|зразок| 8.3.
,
,
.
Функція:
– називається функцією
Ейлера.
Якщо
– просте число, то
,
і взагалі
.
Можна показати, що
,
де
– всі прості дільники n.
Приклад|зразок| 8.4.
,
,
.
,
,
.
Теорема
8.1. (Ейлера).
Якщо
,
то
.
Приклад|зразок|
8.5. Хай|нехай|
n=10.
Тоді і
.
,
,
,
.
З|із| теореми Ейлера безпосередньо виводиться
Теорема
8.2. (мала
теорема Ферма). Якщо
,
то
.
Має місце наступне|таке| твердження|затвердження|
Теорема
8.3. Якщо
числа
попарно взаємно прості, число
– їх добич|добуток|,
x і а – цілі числа, то
.
Останнє твердження|затвердження| є|з'являється,являється| слідством|наслідком| теореми, яка відома як «китайська теорема про залишки».
Приклад|зразок|
8.6. Хай|нехай|
n=10=
;
x=81;
a=61.
Тоді
, 
, 
,
, 
, 
.
Шифрування з|із| відкритим|відчиненим| ключем|джерелом|
Шифрування з|із| відкритим|відчиненим| ключем|джерелом| проводиться|виробляється,справляється| таким чином.
Одержувачем повідомлень|сполучень| проводиться|виробляється,справляється| генерація відкритого|відчиненого| ключа|джерела| (пара чисел n і e) і закритого|зачиненого| ключа|джерела| (число d). Для цього:
вибираються два прості числа p і q;
визначається перша частина|частка| відкритого|відчиненого| ключа|джерела| n=pq;
визначається друга частина|частка| відкритого|відчиненого| ключа|джерела| – вибирається невелике непарне число e, взаємно простої з|із| числом
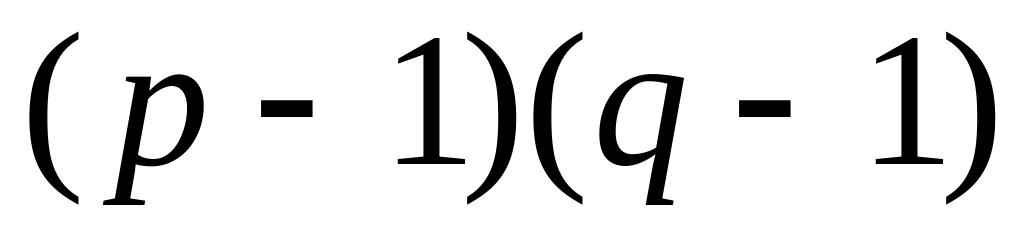(відмітимо|помітимо|,
що
);визначається закритий|зачинений| ключ|джерело|:
.
Після чого відкритий|відчинений| ключ|джерело| (числа n і e) повідомляється всім відправникам повідомлень|сполучень|.
Відправник шифрує повідомлення|сполучення| (розбиваючи його, якщо потрібно, на слова завдовжки менш
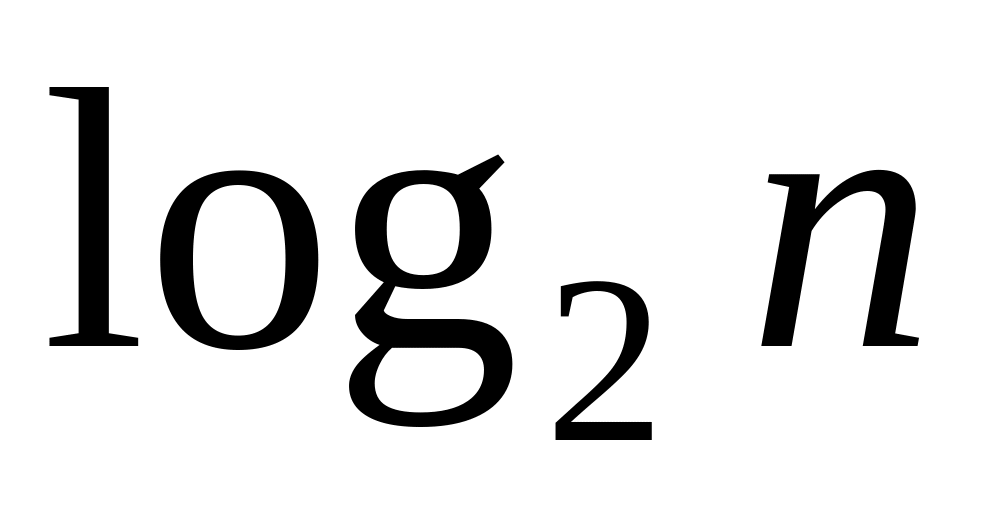розрядів):
,
і відправляє|відряджає| одержувачу.
Одержувач розшифровує повідомлення|сполучення| за допомогою закритого|зачиненого| ключа|джерела| d:
.
Теорема
8.4. Шифрування
з|із|
відкритим|відчиненим|
ключем|джерелом|
коректно, тобто|цебто|
в прийнятих позначеннях
.
Доказ.
Очевидно, що
.
Покажемо, що
.
Дійсно числа d
і
e
взаємно
зворотні по модулю, тобто|цебто|
при
деякому.
Якщо
,
то по малій теоремі Ферма маємо:
.
Якщо
,
то порівняння
,
очевидно, виконується. Таким чином
.
Абсолютно|цілком| аналогічно маємо
.
І по слідству|наслідку| до китайської теореми про залишки
.
Оскільки
і
,
укладаємо|ув'язнюємо,замикаємо,поміщаємо|,
що
.
Приклад|зразок| 8.7. Генерація ключів|джерел|:
p=3, q=11;
n=
;
,
e=7;d= , (
).
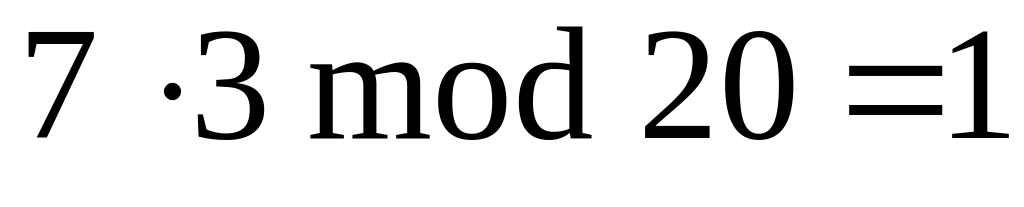Хай|нехай|
=3,
=1,
=2
(
).
Тоді код визначається таким чином:
;
;
.
При розшифровці маємо:
,
,
.
Шифри з|із| відкритим|відчиненим| ключем|джерелом| порівняно прості в реалізації, дуже практичні (оскільки немає необхідності пересилати по каналах зв'язку закритий|зачинений| ключ|джерело| і можна безпечно зберігати його в одному місці) і в той же час володіють високою криптостійкістю.
Здається|видається|, що дешифрувати повідомлення|сполучення| нескладно: досить розкласти відкрито|відчинений| опубліковане число n на множники, відновивши числа p і q, і далі можна легко обчислити|обчисляти,вичислити| секретний ключ|джерело| d.
Проте|однак| справа|річ| полягає в наступному|слідуючому|. В даний час|нині| відомі ефективні алгоритми визначення простоти чисел, які дозволяють за декілька хвилин підібрати|добрати| пару дуже великих простих чисел (по 100 і більше цифр в десятковому записі). В той же час невідомі ефективні алгоритми розкладання дуже великих чисел на множники. Розкладання на множники числа в 200 і більше цифр зажадало б сотень років роботи найкращого суперкомп'ютера. При практичному застосуванні|вживанні| шифрів з|із| відкритим|відчиненим| ключем|джерелом| використовують дійсно великі прості числа (не менше 100 цифр в десятковому записі, а звичайно – значно більше|значно більший|). В результаті розкрити|розітнути| цей шифр виявляється|опиняється| неможливо, якщо не існує ефективних алгоритмів розкладання на множники.
Втім, можливість|спроможність| відкриття|відчинення| таких алгоритмів існує, хоча цей факт і не доведений строго|суворо|.