4. Перешкодостійке кодування

Хай|нехай| є|наявний| канал зв'язку C, що містить|утримує| джерело перешкод:

,

де S – безліч переданих, а – відповідна безліч прийнятих по каналу повідомлень|сполучень|. Кодування F, що володіє такою властивістю, що

,

називається перешкодостійким.

Якщо A=B={0,1}, то помилки в каналі можуть бути наступних|слідуючих| типів:

• 0 1, 1 0 – помилка типу заміщення розряду;

• 0 , 1 – помилка типу випадання розряду;

• 1, 0 – помилка типу вставки розряду.

Хай|нехай| – безліч слів, які можуть бути одержані|отримані| із|із| слова s в результаті|унаслідок,внаслідок| всіх можливих комбінацій допустимих в каналі помилок , тобто|цебто| . Якщо , то та конкретна послідовність помилок, яка дозволяє одержати|отримати| із|із| слова s слово , позначається|значиться| . Якщо тип можливих помилок в каналі мається на увазі, то індекс не указується|вказується|.

Теорема 7.3. Щоб існувало перешкодостійке кодування з|із| виправленням всіх помилок, необхідне і досить|достатньо|, щоб , тобто|цебто| необхідне і досить|достатньо|, щоб існувало розбиття множини|безлічі| B* на множини |безліч|, таке що .

Доказ. Якщо кодування перешкодостійке, то очевидно, що . Назад: по розбиттю будується функція .

Розглянемо|розгледимо| множину|безліч| зі|із| всіх двійкових послідовностей (векторів), що мають вигляд|вид|

.

Введемо|запровадимо| в множині|безлічі| операцію складання +, визначивши для послідовностей і їх суму за допомогою співвідношення: , де – це сума по модулю два.

Відстань Хеммінга між кодовими словами визначається як число позицій таких, що . При побудові|шикуванні| вектора пари однакових двійкових символів даватимуть 0, а пари різних двійкових символів даватимуть 1.

Приклад|зразок| 7.4. (0, 1, 0, 1)+(1, 1, 1, 0)=(1, 0, 1, 1).

Тому відстань Хеммінга можна визначити як число компонент вектора, які рівні 1.

Введена|запроваджена| таким чином відстань Хеммінга задовольняє наступним|слідуючим| умовам:

• 

• ;

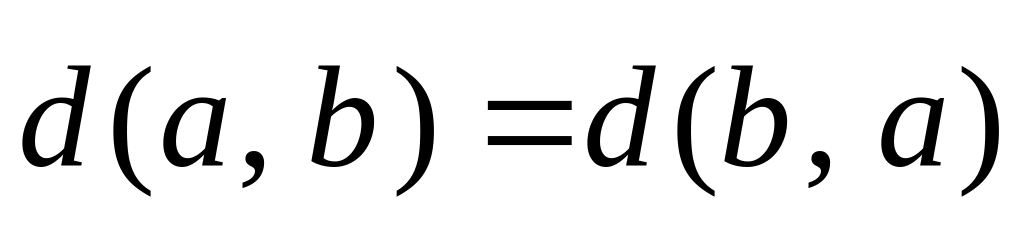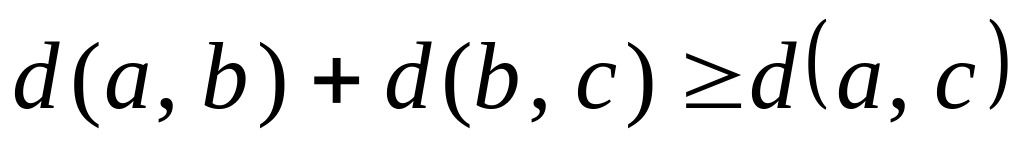• – «нерівність трикутника».

У загальному|спільному| випадку відстанню називають функцію, що задовольняє вищенаведеним умовам. Цим умовам, зокрема, задовольняє геометричну відстань між двома крапками|точками| ( ) і ( ) на площині|плоскості|: .

За наявності біт можна побудувати|спорудити| кодових слів. Проте|однак| часто потрібні не всі з|із| цих слів. Якщо використовувати тільки|лише| частину|частку| кодових слів, то за допомогою перевірок на парність і інших прийомів можна виявити помилки і навіть їх виправляти|справляти|.

Припустимо|передбачимо|, що з|із| використовуються тільки|лише| слів: . Якщо ці слова такі, що при всіх :

, (7.1)

то можна виправляти|справляти| будь-які помилки кратності .

Допустимо, що в деяких компонентах слова при передачі виникли помилки, в результаті|унаслідок,внаслідок| яких символи 0 були прийняті як 1, а символи 1 – як 0 (помилки типу заміщення). Слово , що вийшло в результаті, знаходиться|перебуває| на відстані від слова . Отже, якщо вважати|лічити|, що помилки при передачі можуть виникати не більше ніж в компонентах, то сукупність всіх слів, які можуть вийти з |із|, є множина|безліч| .

З|із| нерівності трикутника і умови (7.1) виходить , якщо тільки|лише| . Дійсно, допустимо, що існує слово . Тоді і .

Згідно нерівності трикутника

,

що приводить|призводить,наводить| до суперечності|протиріччя| з|із| умовою (7.1).

Множина|безліч| називається областю декодування для слова . Оскільки|тому що| області декодування не перетинаються, то при прийомі слова з|із| області декодування можна вважати|лічити|, що передавалося слово . Якщо при цьому число помилок не перевершує, то при прийомі завжди ухвалюватиметься правильне рішення.

Оскільки|тому що| число елементів в множині|безлічі| рівне числу способів вибору деяких ( ) компонент слова , то

.

Далі, оскільки |тому що|, то: , тобто|цебто|

. (7.2)

Нерівність (7.2) називається межею|кордоном| Хеммінга. Воно дає оцінку зверху для числа кодових слів, які можна використовувати для передачі, якщо їх довжина рівна біт і потрібно виправляти|справляти| всі - кратні помилки.

Приклад|зразок| 7.5. Хай|нехай| =8, тоді . Оскільки , то ; ; ; ; .

Якщо =4, то .

Якщо =3, то .

Якщо =2, то .

Якщо =1, то .

Якщо =0, то .

Таким чином, якщо зустрічаються тільки|лише| одиночні помилки типу заміщення, то при використанні 8 біт можна безпомилково передавати 28 слів. У загальному|спільному| випадку, якщо є|наявний| біт і потрібно виправляти|справляти| одиночні помилки типу заміщення, то межа|кордон| Хеммінга визначається наступним|слідуючим| виразом|вираженням|, який є приватним випадком формули|з'являється,являється| (7.2):

. (7.3)

Позначимо мінімальне число біт, необхідне для передачі слів, буквою|літерою| . Тоді: , і з|із| формули (7.3) виходить

. (7.4)

Таким чином, для перешкодостійкого кодування сигналів при одиночних помилках типу заміщення необхідно використовувати додаткові біт, кількість яких повинна задовольняти умові (7.4). Даний випадок простий, але|та| одночасно практично дуже важливий|поважний|. Такою властивістю, як правило, володіють внутрішні шини передачі даних в сучасних комп'ютерах.

Приклад|зразок| 7.6. Для повідомлення|сполучення| завдовжки буде потрібно додаткових розрядів, оскільки 64= .

Код, в якому використовуються додаткові розряди для перешкодостійкої передачі сигналів, називається кодом Хеммінга.